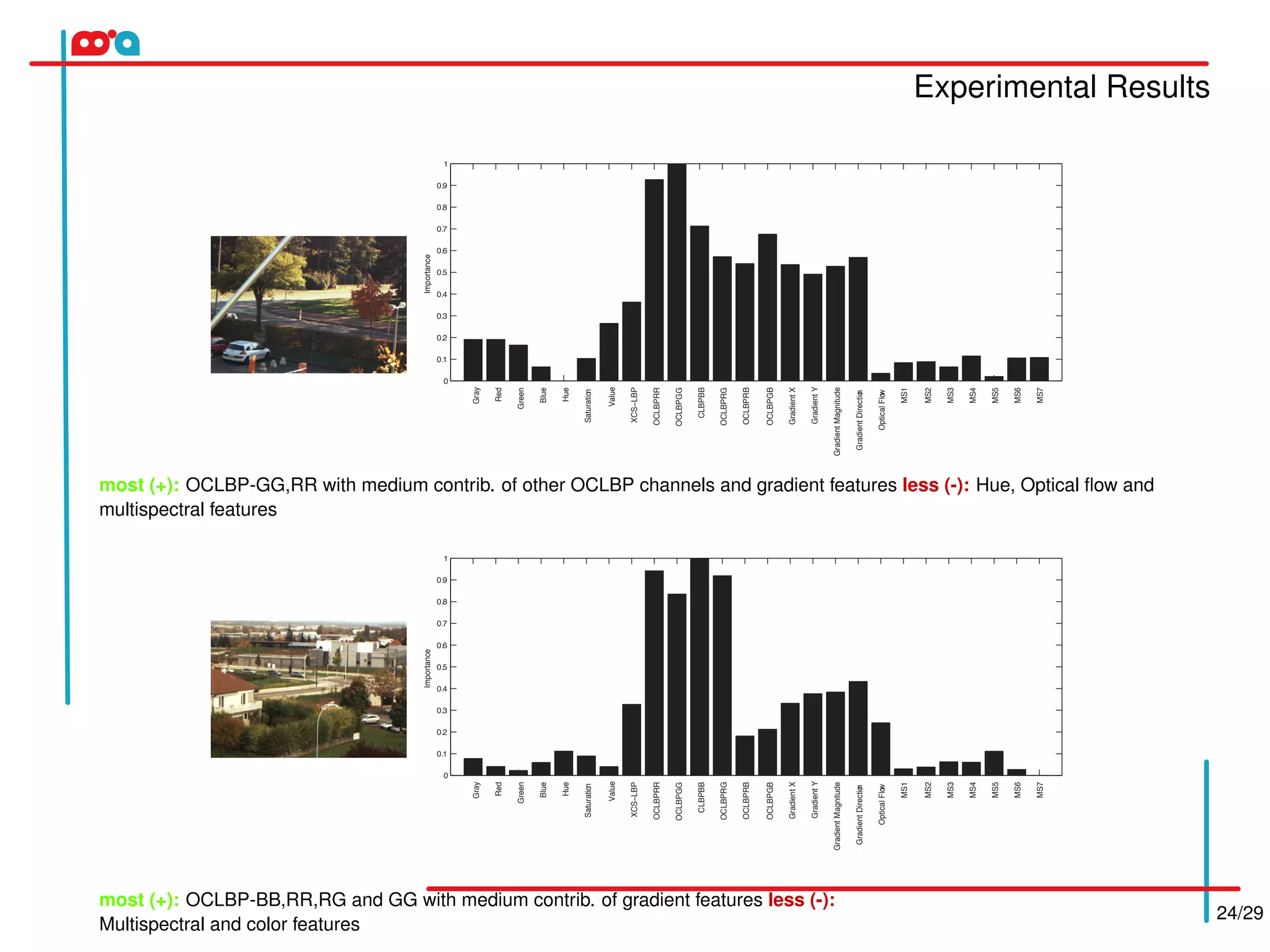
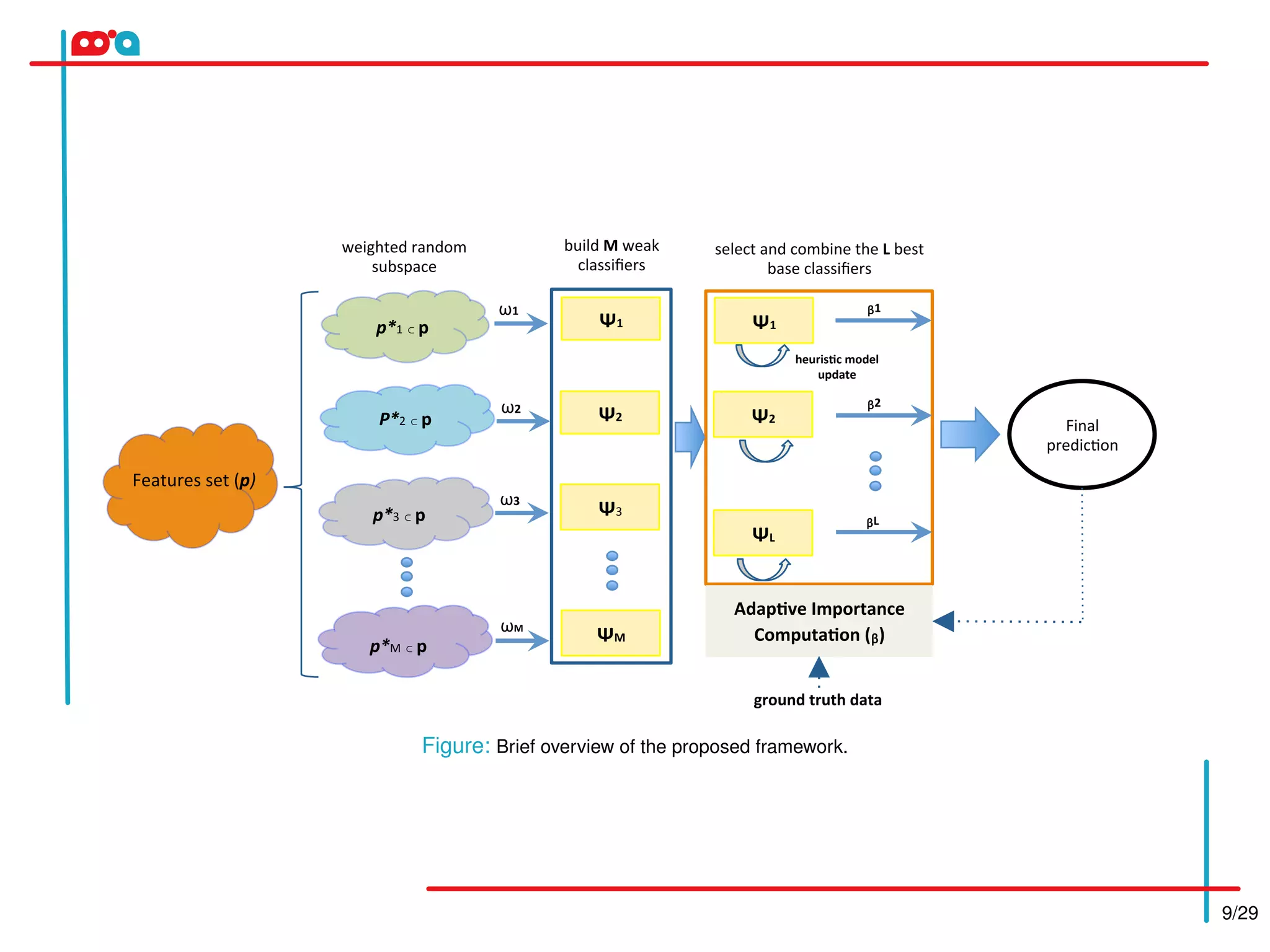
The proposed method uses an online weighted ensemble of one-class SVMs for feature selection in background/foreground separation. It automatically selects the best features for different image regions. Multiple base classifiers are generated using weighted random subspaces. The best base classifiers are selected and combined based on error rates. Feature importance is computed adaptively based on classifier responses. The background model is updated incrementally using a heuristic approach. Experimental results on the MSVS dataset show the proposed method achieves higher precision, recall, and F-score than other methods compared.

1. Online Weighted One-Class Ensemble for Feature Selection in
Background/Foreground Separation
Caroline Silva, Thierry Bouwmans, Carl Fr´elicot, Micka¨el Coustaty
December 6th, 2016 - Mexico

2. Summary
2/29
1 Introduction
2 Proposed Work
3 Experimental Results
4 Conclusion and Future Works

3. Introduction
3/29
Background Subtraction
Ini$alize
Backgrounwd Model
Background Model
Maintenance
Foreground
Detec$on
Model
Input Stream Output Masks
Figure: Block diagram of the background subtraction process.

4. Introduction
4/29
Background Subtraction
Background subtraction is a widely used approach for detecting moving objects from static
cameras.
Figure: Moving object tracking results.

5. Introduction
5/29
Why is it interesting today
X1
X2
X3
X4X5
Figure: Given a complex scene with different regions X1, X2, X3, X4 and X5, each region can be characterized
by different features such as: texture, color, texture-color, motion and edge.
Common methods
Same feature is used globally for the whole scene.
Key challenges
It requires a deep knowledge of the scene.
It is possible to automatically select the most relevant features

6. Introduction
6/29
Feature Selection
Traditionally, feature selection methods can be categorized into three main groups:
Wrapper-based methods
• employ a classification algorithm as a “black box” for selecting a set of relevant features.
Embedded methods
• the feature selection is incorporated as part of the classification algorithm, such as in
the decision trees or in neural networks.
Filter-based methods
• evaluate the relevance of the features based on a statistical measure estimated directly
from the data.
Ensemble-based approaches for feature selection

7. Summary
7/29
1 Introduction
2 Proposed Work
3 Experimental Results
4 Conclusion and Future Works

8. Proposed Work
8/29
N
u
m
b
e
r
o
f
fra
m
e
s
200
150
Frames
100
50
0
Feature Importance
Motion
Gradient
Color+Texture
Features
Texture
Color
0.6
1
0.8
0.4
0
0.2
Importance
Figure: Illustration of a complex scene (left) and its features
importance over time. The bar-graph (right) shows the feature
importance variations for a certain region of the scene along
time. The color, texture, cor-texture, gradients and motion
features are represented by pink, blue, pale orange, green and
dark orange color, respectively.
We propose an online weighted ensemble
of one-class SVMs (Support Vector
Machines) for foreground-background
separation.
It automatically selects the best features
for different regions of the image, and the
more relevant features are used for
foreground segmentation.

9. 9/29
ω1
ω3
Ψ1
Ψ2
Ψ3
Final
predic.on
Features set (p)
weighted random
subspace
p*1 ⊂ p
P*2 ⊂ p
p*3 ⊂ p
build M weak
classifiers
ω2
p*M ⊂ p
Ψ1
ᵦ1
Ψ2
ΨL
select and combine the L best
base classifiers
Adap,ve Importance
Computa,on (ᵦ)
ground truth data
heuris,c model
update
ΨM
ωM
ᵦ2
ᵦL
Figure: Brief overview of the proposed framework.

10. Proposed Work
10/29
An Online Weighted One-Class Ensemble for Feature Selection
A. Generate multiple base models
N
u
m
b
e
r
o
f
fra
m
e
s
This above approach increases the diversity of base
classifiers since different weights of each random sub-
space are taken to distinguish the decision boundaries
computed by the classifiers.
Algorithm 1 Generate multiple base background models
1: Require: IWOC-SVM training procedure, training sequence X, subspace dimension p∗, number of base classifiers M, weight
distribution δ(x)
2: k ← 1
3: repeat
4: Sk ← SelectRandomSubspace(X,p∗)
5: Train k-th IWOC-SVM on Sk with respect to weights w ∼ δ(x)
6: k ← k+1
7: until k > M
8: Output: trained IWOC-SVM base classifiers Ψ = {Ψ1,Ψ2,...,ΨM }

11. Proposed Work
11/29
How to Choose the Classifier?
Bicego and Figueiredo, 2009 proposed a Weighted version that allow to use weights W = {w1,...,wN } in [0,1]
for the data.
R
R
R
a
wiξi
target
outlier
xi
Weighted One-Class SVM (WOC-SVM)
Minimizing the hypersphere volume implies the
minimization of R2
. To prevent the classifier from
over-fitting with noisy data, slack variables ξi are
introduced to allow some target points (respectively
outliers) outside (respectively inside) the hypersphere.
Therefore the problem is to minimize:
Θ(a,R) = R2
+C
N
∑
i=1
wi ξi (1)
where C is a user-defined parameter that controls the
trade-off between the volume and the number of
target points rejected. The larger C, the less outliers
in the hypersphere.
The BS task requires adjust the learned model to the scene variations over time

12. 12/29
Why update the background model?

13. Proposed Work
13/29
An Incremental Weighted One-Class SVM (IWOC-SVM)
We propose an IWOC-SVM which is closely related to the procedure proposed by Tax and Laskov (2003).
Given new samples Z1 = {x1,x2,...,xs} and its
respective weights not learned by the IWOC-SVM.
Karush-Kuhn-Tucker (KKT) conditions:
αi = 0 ⇒ ||xi −a||2
< R2
(2)
0 < αi < C ⇒ ||xi −a||2
= R2
(3)
αi = C ⇒ ||xi −a||2
> R2
(4)
The mathematical model can be defined as:
R −θ ≤ ||x −a||≤ R (5)
where θ ∈ [0,R] is relative to the distribution of
previous training set.
R
R
R
a
wiξi
target
outlier
xi
Algorithm 2 Incremental Weighted One-Class SVM
1: Require: Previous training set Z0, newly added training set Z1 and its respective weights
2: Train IWOC-SVM classifier on Z0, then split Z0 = SV0 ∪NSV0
3: Input new samples Z1. Put samples that violate KKT conditions in ZV
1 . If ZV
1 = /0, then goto 2.
4: Put samples from NSV0 that satisfy Eq. (5) into NSVS
0 .
5: Set Z0 = SV0 ∪NSVS
0 ∪ZV
1 and train IWOC-SVM classifier on Z0.
6: Output: IWOC-SVM classifier Ω and the new training set Z0.
.

14. Proposed Work
14/29
B. Selection of the best base classifiers
Let λcorrect
k (respectively λwrong
k ) be the number of times a pixel was correctly (respectively uncorrectly) classified
by the k-th (k = 1,...,M) base classifier from given ground truth data. Then, the corresponding error is given by:
errork =
λwrong
k
λcorrect
k +λwrong
k
(6)
Note that only the base classifiers that have the smallest errors are combined and used to differentiate the
moving objects from the background model in the scene.

15. 15/29
The Algorithm 3 was adapted from the algorithm proposed by (Wozniak, 2013)
Algorithm 3 Adaptive Importance (AI) computation
1: Require: Strong classifier H, validation set (t1,y1),...,(tN ,yN ) where ti ∈ T, yi ∈ Y = 0,1 for background and foreground
examples respectively, set of L best base classifiers Ψ = {Ψ1,Ψ2,...,ΨL}, learning rate parameter γ
2: Initialize all L best classifiers with importance: βl = 1
3: repeat
4: Classify ti using the strong classifier H according to Eq. (9)
5: for l = 1 : L do
6: Checks response of Ψl and calculates their errorl according to Eq. (6)
7: For each best classifier, Ψl , update the importance βl = βl (i −1)+
Pa(Ψl )−Pa(Ψl (i−1))
(N+γ)
8: where Pa(Ψl ) = 1 −errorl according to Eq.(6).
9: end for
10: until i < N
11: Normalize the importance β of each L best classifier.
12: Output: New importance assigned to the best classifiers β = {β1,β2,...,βL}

16. Proposed Work
16/29
C. Background Detection
Given an incoming pixel x to be classified, one can define a support function associated to the target class ω for
each of the L best base classifiers: ∀l = 1,...,L
Fl (x,ω) =
1
s1
exp(−d(x,a)/s2) (7)
where d(x,a) is a distance metric from x to the center a of the target class ω, s1 is a normalization factor and s2
is a scale parameter. Each Fl (x,ω) is then compared to a threshold t1 to obtain the positive or negative class
labels:∀l = 1,...,L
cl (x,ω) =
1 if Fl (x,ω) t1
−1 otherwise
(8)
Comparing the weighted sum of theses L class labels as in (Tax and Duin, 2001) to another threshold t2 allows
to define the strong classifier for x as follows:
H(x) =
1 if 1
L ∑L
l=1 βl cl (x,ω) t2
0 otherwise
(9)
A pixel x is classified as a background pixel if H(x) = 0.

17. Proposed Work
17/29
D. Heuristic approach for Background Model Maintenance
The Small Votes Instance Selection (SVIS) introduced by Guo and Boukir (Guo and Boukir, 2015) consists of an
unsupervised ensemble margin that combines the first c(1) and second most voted class c(2) labels under the
learned model. Let vc(1)
and vc(2)
denote the relative number of votes. Then the margin, taking value in [0,1] is:
m(x) =
vc(1)
−vc(2)
L
(10)
where L represents the number of best base classifiers in the ensemble. The first smallest margin instances are
selected as support vector candidates. The strong model is updated by the first smallest margin instances. This
procedure is presented in the Algorithm 4.
This heuristic significantly reduces the IWOC-SVM training task complexity while maintaining the accuracy of the
IWOC-SVM classification.

18. Proposed Work
18/29
Algorithm 4 Heuristic approach for model maintenance
1: Require: strong classifier H, test set Z = {z1,z2,...,zt }, weight distribution δ(z), user defined parameter time, user defined
parameter η.
2: i ← 1
3: repeat
4: if H(zi ) = 1 (background) then
5: Compute the margin m(zi ) by Eq. (10).
6: end if
7: if time is reached then
8: Order all the test instances according to their margin values, in ascending order.
9: The η smallest margin instances are selected as support vectors.
10: H(x) is updated using Z1 and its weight w ∼ δ(x).
11: end if
12: i ← i +1
13: until i > t

19. Summary
19/29
1 Introduction
2 Proposed Work
3 Experimental Results
4 Conclusion and Future Works

20. Experimental Results
20/29
Dataset
MSVS dataset (Benezeth et al., 2014) which consists of a set of 5 video sequences containing 7
multispectral bands and color video sequence (RGB).
Parameter Settings
IWOC-SVM with RBF (Radial Basis Function) kernel as a base classifier with C = 1.
The pool of classifiers was homogeneous and consisted of 10 base classifiers of the same type.
The classification threshold t1 was set to 0.9 and t2 to 0.5 for combining the best one-class classifiers.
Video sequences were resized to 160 ×120
The p* = 5 for the random subspace dimension from the original p = 26-dimensional.
Features: Color features (R,G,B, H,S,V and gray-scale), texture feature (XCS-LBP), color-texture
(OC-LBP), edge feature (gradient orientation and magnitude), motion feature (optical flow) and
multispectral bands (7 spectral narrow bands).

21. Experimental Results
21/29
MSVS dataset
Figure: Background subtraction results using the MSVS dataset – (a) original frame, (b) ground truth and (c) proposed method.
The true positives (TP) pixels are in white, true negatives (TN) pixels in black, false positives (FP) pixels in red and false negatives
(FN) pixels in green.

22. Experimental Results
22/29
Table: Performance of the different methods using the MSVS data set.
Videos Method Precision Recall F-score
Scene
01
MD (RGB)(Benezeth et al., 2014) 0.6536 0.6376 0.6536
MD (MSB)(Benezeth et al., 2014) 0.7850 0.8377 0.8105
Pooling (MSB)(Benezeth et al., 2014) 0.7475 0.8568 0.7984
Proposed 0.8500 0.9580 0.9008
Scene
02
MD (RGB)(Benezeth et al., 2014) 0.8346 0.9100 0.8707
MD (MSB)(Benezeth et al., 2014) 0.8549 0.9281 0.8900
Pooling (MSB)(Benezeth et al., 2014) 0.8639 0.8997 0.8815
Proposed 0.8277 0.8245 0.8727
Scene
03
MD (RGB)(Benezeth et al., 2014) 0.7494 0.5967 0.6644
MD (MSB)(Benezeth et al., 2014) 0.7533 0.6332 0.6889
Pooling (MSB)(Benezeth et al., 2014) 0.8809 0.5134 0.6487
Proposed 0.9056 0.9953 0.9483
Scene
04
MD(RGB)(Benezeth et al., 2014) 0.8402 0.7929 0.8158
MD (MSB)(Benezeth et al., 2014) 0.8430 0.8226 0.8327
Pooling (MSB)(Benezeth et al., 2014) 0.8146 0.8654 0.8392
Proposed 0.9534 0.8374 0.8997
Scene
05
MD (RGB)(Benezeth et al., 2014) 0.7359 0.7626 0.7490
MD (MSB)(Benezeth et al., 2014) 0.7341 0.8149 0.7724
Pooling (MSB)(Benezeth et al., 2014) 0.7373 0.8066 0.8066
Proposed 0.7316 0.8392 0.8400
*MD = Mahalanobis distance

23. Experimental Results
23/29
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Importance
Gray
Red
Green
Blue
Hue
Saturation
Value
XCS−LBP
OCLBPRR
OCLBPGG
CLBPBB
OCLBPRG
OCLBPRB
OCLBPGB
GradientX
GradientY
GradientMagnitude
GradientDirection
OpticalFlow
MS1
MS2
MS3
MS4
MS5
MS6
MS7
Scene 01
most (+): Gradient Direction with medium contrib. multispectral features less (-): OCLBP-GB
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Importance
Gray
Red
Green
Blue
Hue
Saturation
Value
XCS−LBP
OCLBPRR
OCLBPGG
CLBPBB
OCLBPRG
OCLBPRB
OCLBPGB
GradientX
GradientY
GradientMagnitude
GradientDirection
OpticalFlow
MS1
MS2
MS3
MS4
MS5
MS6
MS7
most (+): MS1,MS2 and MS6 with Color, Gradient X features less (-): XCS-LBP and MS4

24. Experimental Results
24/29
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Importance
Gray
Red
Green
Blue
Hue
Saturation
Value
XCS−LBP
OCLBPRR
OCLBPGG
CLBPBB
OCLBPRG
OCLBPRB
OCLBPGB
GradientX
GradientY
GradientMagnitude
GradientDirection
OpticalFlow
MS1
MS2
MS3
MS4
MS5
MS6
MS7
most (+): OCLBP-GG,RR with medium contrib. of other OCLBP channels and gradient features less (-): Hue, Optical flow and
multispectral features
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Importance
Gray
Red
Green
Blue
Hue
Saturation
Value
XCS−LBP
OCLBPRR
OCLBPGG
CLBPBB
OCLBPRG
OCLBPRB
OCLBPGB
GradientX
GradientY
GradientMagnitude
GradientDirection
OpticalFlow
MS1
MS2
MS3
MS4
MS5
MS6
MS7
most (+): OCLBP-BB,RR,RG and GG with medium contrib. of gradient features less (-):
Multispectral and color features

25. Experimental Results
25/29
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Importance
Gray
Red
Green
Blue
Hue
Saturation
Value
XCS−LBP
OCLBPRR
OCLBPGG
CLBPBB
OCLBPRG
OCLBPRB
OCLBPGB
GradientX
GradientY
GradientMagnitude
GradientDirection
OpticalFlow
MS1
MS2
MS3
MS4
MS5
MS6
MS7
most (+): OCLBP-RR with high contrib. of other OCLBP channels and multispectral features less (-): Gradient Magnitude

26. Summary
26/29
1 Introduction
2 Proposed Work
3 Experimental Results
4 Conclusion and Future Works

27. Conclusion and Future Works
27/29
Conclusion
An incremental version of the WOC-SVM algorithm, called Incremental Weighted One-Class Support
Vector Machine (IWOC-SVM).
An online weighted version of random subspace (OW-RS) to increase the diversity of the classifiers pool.
A mechanism called Adaptive Importance Calculation (AIC) to suitably update the relative importance of
each feature over time.
A heuristic approach for IWOC-SVM model updating to improve speed.
Future Works
A superpixel segmentation strategy to improve the segmentation performance, increasing the
computational efficiency of our ensemble.
An unsupervised mechanism to suitably update the importance of each feature discarding insignificantly
features over time without ground-truth data.

28. 28/29
THANK YOU!!!

29. References
29/29
Benezeth, Y., Sidibe, D., and Thomas, J. B. (2014). Background subtraction with multispectral video sequences. In IEEE International Conference on Robotics and
Automation (ICRA).
Guo, L. and Boukir, S. (2015). Fast data selection for SVM training using ensemble margin. Pattern Recognition Letters (PRL), 51.
Tax, D. and Duin, R. (2001). Combining one-class classifiers. In Proceedings of the Second International Workshop on Multiple Classifier Systems (MCS), pages
299–308.
Tax, D. and Laskov, P. (2003). Online SVM learning: from classification to data description and back. In IEEE Workshop on Neural Network for Signal Processing
(NNSP), pages 499–508.
Wozniak, M. (2013). Hybrid classifiers: methods of data, knowledge, and classifier combination. Springer Publishing Company, Incorporated.