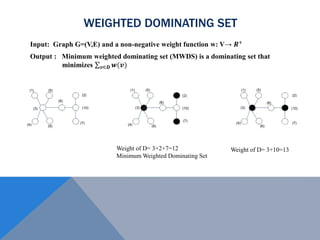
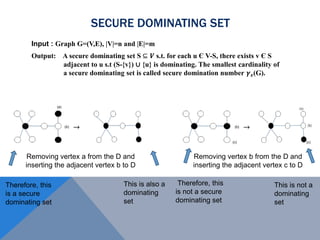
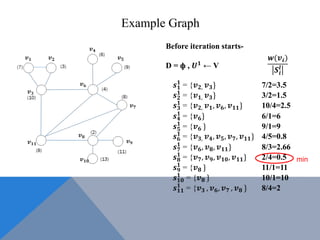
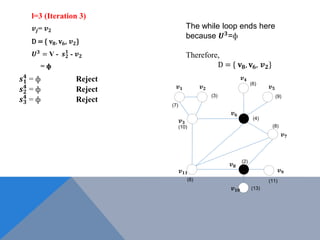
The document discusses weighted secure domination in graphs. It begins by defining domination number and weighted domination number. It proposes a greedy algorithm that provides a 1 + log(n) approximation for weighted domination number. The algorithm works by iteratively selecting the unselected vertex with the minimum ratio of weight to number of uncovered neighbors. This achieves an approximation ratio of H(n), which is at most 1 + log(n). The algorithm runs in polynomial time.

1. STUDY OF WEIGHTED SECURE
DOMINATION IN GRAPHS
B Y
M A H E S H K U M A R G A R H W A L

2. Problem Statement
Our goal is to determine the
computational complexity of weighted
secure domination problem and designing
efficient algorithm for weighted secure
domination number

3. Starting with Basics
Input: Graph G=(V,E), |V|=n and |E|=m.
Output: Subset D of V s.t. each vertex of G either belongs to D or has a
neighbour in D. Minimum cardinality of D is called the
Domination number γ(G) f G.
DOMINATING SET
Complexity :
The dominating set problem concerns testing whether γ(G) ≤ K for a
given graph G and input K; it is classical NP-complete decision problem
in computational complexity theory

4. BOUND ON DOMINATION NUMBER
Let G be a graph with n ≥ 1 vertices and let Δ be the maximum degree of the graph.
The following bounds on γ (G) are known :
One vertex can dominate at most Δ other vertices; therefore γ(G) ≥ n/(1 + Δ).
The set of all vertices is a dominating set in any graph; therefore γ(G) ≤ n.
If there are no isolated vertices in G, then there are two disjoint dominating sets
in G. Therefore in any graph without isolated vertices it holds that γ(G) ≤ n/2.

5. DOMINATING SET AND SET COVERING PROBLEM
Given a graph G = (V, E) with V = {1, 2, ..., n}, construct a set cover
instance (U, S) as follows: the universe U is V, and the family of
subsets is S = {S1, S2, ..., Sn} such that Sv consists of the vertex v
and all vertices adjacent to v in G.
Now if D is a dominating set for G, then C = {Sv : v ∈ D} is a feasible
solution of the set cover problem, with |C| = |D|. Conversely,
if C = {Sv : v ∈ D} is a feasible solution of the set cover problem, then D
is a dominating set for G, with |D| = |C|.
Hence the size of a minimum dominating set for G equals the size of a
minimum set cover for (U, S).

6. Why Dominating Set?
 Historical roots to the
problem of determining
the minimum number of
queens required to
dominate the 8 x 8
chess board.
 Social Networking
Theory: To determine
the positive influence
that is possessed by
an individual as well
as impact on the
neighbours.
 Minimal power
consumption in
Wireless Sensor
network.

7. WEIGHTED DOMINATING SET
Input: Graph G=(V,E) and a non-negative weight function w: V→ 𝑹+
Output : Minimum weighted dominating set (MWDS) is a dominating set that
minimizes 𝒗∈𝑫 𝒘(𝒗)
(1)
(4)
(3)
(1)
(8)
(4)
(2)(2)
(10)
(7)
(7)
(7)
(6)
(5)
(10)
(2)
(10)
(4)
(5)(1)
(6)
(8)
(5)
(3)
(8)
(6)
(3)
Weight of D= 3+2+7=12
Minimum Weighted Dominating Set
Weight of D= 3+10=13

8. Why Weighted Dominating Set?
 Applications are seen in Twitter Network where weights of vertices
could be interpreted as the costs of getting those individuals on board
for a campaign or a behaviour change intervention

9. SECURE DOMINATING SET
Input : Graph G=(V,E), |V|=n and |E|=m
Output: A secure dominating set S ⊆ 𝑽 s.t. for each u Є V-S, there exists v Є S
adjacent to u s.t (S-{v}) ∪ {u} is dominating. The smallest cardinality of
a secure dominating set is called secure domination number 𝜸 𝒔(G).
(a)
(b) →
Removing vertex a from the D and
inserting the adjacent vertex b to D
This is also a
dominating
set
Therefore, this
is a secure
dominating set
→(b)
(c) (c)
Removing vertex b from the D and
inserting the adjacent vertex c to D
Therefore, this
is not a secure
dominating set
This is not a
dominating
set

10. WEIGHTED SECURE DOMINATING SET
Input: Graph G=(V,E) and a non-negative weight
function w: V→ 𝑹+
Output : Minimum weighted dominating set
(MWSDS) is a secure dominating set that
minimizes 𝒗∈𝑺 𝒘(𝒗)

11. Prior Work done in this field
• A (4+Є)-approximation algorithm has been presented for Weighted Dominating
set based on dynamic programming for Min-weighted Chromatic Disk Covers by
Feng Zoua , Yuexuan Wang , Xiao-Hua Xuc, Xianyue Li , Hongwei Duc ,
Pengjun Wanc , Weili Wu(2011).
• A (1+ Є)- approximation algorithm has been presented for Weighted Connected
Dominating set in the same paper.
• Fomin, Grandoni & Kratsch (2009) show how to find a minimum dominating set
in time O(1.5137n) and exponential space, and in time O(1.5264n) and polynomial
space.
• A faster algorithm, using O(1.5048n) time was found by van Rooij, Nederlof &
van Dijk (2009), who also show that the number of minimum dominating sets can
be computed in this time.
• The number of minimal dominating sets is at most 1.7159n and all such sets can
be listed in time O(1.7159n) (Fomin et al. 2008)

12. Prior Work done in this field
• Two algorithms were presented in the paper by AP Burger, AP de Villiers & JH
van Vuurenin 2012 for computing the secure domination number of a general
graph
Their first algorithm follows a branch-and reduce approach and was presented
and illustrated by means of an example in section 4. Their second algorithm follows
a classical branch-and-bound approach and was presented and illustrated by means
of the same example in section 5.
• It is shown in our base paper that the problem of Secure Domination in Split and
Bipartite graphs is NP-complete

13. We have gone through following research papers.

14. Phase 1 is the step in which we have to devise an approximation algorithm for
Minimum Weighted domination set for a graph.
We have proposed an algorithm based on the readings on the paper published
on Approximation for Dominating set with Measure Functions
The reductions show that an efficient algorithm for the minimum dominating
set problem would provide an efficient algorithm for the set cover
problem and vice versa.
Proposed Work

15. More specifically, the greedy algorithm provides a factor 1 + log |V| approximation
of a minimum dominating set, and Raz & Safra (1997) show that no polynomial
time algorithm can achieve an approximation factor better than c log |V| for
some c > 0 unless P = NP.
Dominating Set is a special case of the weighted model when all weights of vertices
and edges are equal to one. Therefore, we have the following conclusion-
 Weighted-Measured Dominating Set problem is NP-hard.
 Approximating Weighted Dominating Set problem within ratio Ω(logn) is NP-
hard.

16. Greedy Algorithm for Weighted Dominating Set
For any given instance of Weighted Dominating Set
problem, let OPT be the size of the optimal solution.
Define Si = {𝒗𝒋 | (𝒗𝒋, 𝒗𝒊) ∈ E(G)} . Let D be the
dominating set generated by the algorithm, and 𝑫 =
V − D. Let 𝑼𝒍 be the set of vertices not dominated so
far at the beginning of iteration l. The greedy
algorithm works as follows.

17. ALGORITHM(CONTINUED)
1. D ← ф, 𝑼 𝟏
← V, l ← 1.
𝟐. 𝒔𝒊
𝒍
← 𝑺𝒊 , for 1≤ i≤ n.
3. Ignore if 𝒔𝒊
𝒍
= ф, Ɐi , 1≤ i≤ n.
4. D ← D ∪ {𝒗𝒊}
5 𝑾𝒉𝒊𝒍𝒆 𝑼𝒍
≠ ф do
𝒂 𝒗𝒋= arg 𝒎𝒊𝒏 𝒗 𝒊Є𝑫
𝒘(𝒗 𝒊)
𝑺 𝒊
𝒍 .
𝒃 D ← D ∪ {𝒗𝒋}
𝒄 𝑼𝒍+𝟏
← 𝑼𝒍
- 𝒔𝒋
𝒍
- 𝒗𝒋
(𝒅) 𝒔𝒊
𝒍+𝟏
← 𝒔𝒊
𝒍
- 𝒔𝒋
𝒍
-𝒗𝒋, for 𝒗𝒊 Є𝑫.
(e) Ignore if 𝒔𝒊
𝒍+𝟏
= ф, Ɐi , 1≤ i≤ n.
(f) l ← l+1.
6. Output Minimum Weighted Dominating Set.

18. Complexity of the algorithm
The above greedy algorithm produces an 𝐻 𝑛 ratio approximation algorithm
for Weighted-Measured Dominating Set problem, where 𝐻 𝑛 = 1 + 1
2 +
…. +1
n .
PROOF
It is easy to see that g(𝑣1) ≤ g(𝑣2) ≤ ··· ≤ g(𝑣 𝑛). In addition, we know that-
𝑖=1
𝑛
𝑔( 𝑣𝑖) = 𝑣 𝑖∈𝐷 𝑤(𝑣𝑖)
For any vertex 𝑣𝑖, assume 𝑣𝑖 is dominated at iteration l, i.e., 𝑣𝑖 ∈ Ul
and 𝑣𝑖 ∉
Ul+1
. Hence, we know that |Ul
| ≥ n − i + 1. Therefore, from the
minimization, we have
𝑔(𝑣𝑖) ≤
𝑂𝑃𝑇
|𝑈 𝑙|
≤
𝑂𝑃𝑇
𝑛−𝑖+1

19. Complexity of the algorithm (Conti.)
where the first inequality is due to at the beginning of iteration l, the
leftover sets of the optimal solution (contained in D) can dominate Ul
at
a cost of at most OPT. Combining (1) and (2), we have
𝑣 𝑖∈𝐷 𝑤(𝑣𝑖) = 𝑖=1
𝑛
𝑔( 𝑣𝑖) ≤ 𝑖=1
𝑛 𝑂𝑃𝑇
𝑛−𝑖+1
= 𝐻 𝑛 . 𝑂𝑃𝑇
It is well known that 𝐻 𝑛 ≤ log n+1, therefore the approximation ratio
produced by greedy algorithm is upper bounded by O (log n). In
addition, we stress that the bound 𝐻 𝑛 is tight.

20. Example Graph
Before iteration starts-
D = ф , 𝑼 𝟏
← V
𝒔 𝟏
𝟏
= {𝒗 𝟐, 𝒗 𝟑} 7/2=3.5
𝒔 𝟐
𝟏
= {𝒗 𝟏, 𝒗 𝟑} 3/2=1.5
𝒔 𝟑
𝟏
= {𝒗 𝟐, 𝒗 𝟏, 𝒗 𝟔, 𝒗 𝟏𝟏} 10/4=2.5
𝒔 𝟒
𝟏
= {𝒗 𝟔} 6/1=6
𝒔 𝟓
𝟏
= {𝒗 𝟔 } 9/1=9
𝒔 𝟔
𝟏
= {𝒗 𝟑, 𝒗 𝟒, 𝒗 𝟓, 𝒗 𝟕, 𝒗 𝟏𝟏} 4/5=0.8
𝒔 𝟕
𝟏
= {𝒗 𝟔, 𝒗 𝟖, 𝒗 𝟏𝟏} 8/3=2.66
𝒔 𝟖
𝟏
= {𝒗 𝟕, 𝒗 𝟗, 𝒗 𝟏𝟎, 𝒗 𝟏𝟏} 2/4=0.5
𝒔 𝟗
𝟏
= {𝒗 𝟖 } 11/1=11
𝒔 𝟏𝟎
𝟏
= {𝒗 𝟖 } 10/1=10
𝒔 𝟏𝟏
𝟏
= {𝒗 𝟑 , 𝒗 𝟔, 𝒗 𝟕 , 𝒗 𝟖 } 8/4=2
𝒘(𝒗𝒊)
𝑺𝒊
𝒍
min

21. l=1 (Iteration 1) l=2 (Iteration 2)
𝒗𝒋= 𝒗 𝟖 𝒗𝒋= 𝒗 𝟔
D = { 𝐯 𝟖} D = { 𝐯 𝟖, 𝐯 𝟔}
𝑼 𝟐
= V - 𝒔 𝟖
𝟏
- 𝒗 𝟖 𝑼 𝟐
= V - 𝒔 𝟔
𝟏
- 𝒗 𝟔
= {𝒗 𝟏, 𝒗 𝟐 , 𝒗 𝟑 , 𝒗 𝟒 , 𝒗 𝟓 , 𝒗 𝟔} ={𝒗 𝟏, 𝒗 𝟐}
𝒔 𝟏
𝟐
= {𝒗 𝟐, 𝒗 𝟑} 7/2=3.5
𝒔 𝟐
𝟐
= {𝒗 𝟏, 𝒗 𝟑} 3/2=1.5
𝒔 𝟑
𝟐
= {𝒗 𝟐, 𝒗 𝟏, 𝒗 𝟔} 10/3=3.33
𝒔 𝟒
𝟐
= {𝒗 𝟔} 6/1=6
𝒔 𝟓
𝟐
= {𝒗 𝟔 } 9/1=9
𝒔 𝟔
𝟐
= {𝒗 𝟑, 𝒗 𝟒, 𝒗 𝟓} 4/3=1.33
𝒔 𝟕
𝟐
= {𝒗 𝟔} 8/1=8
𝒔 𝟗
𝟐
= ф Reject
𝒔 𝟏𝟎
𝟐
= ф Reject
𝒔 𝟏𝟏
𝟐
={𝒗 𝟑 , 𝒗 𝟔} 8/2=4
min
𝒔 𝟏
𝟑
= {𝒗 𝟐 } 7/1=7
𝒔 𝟐
𝟑
= {𝒗 𝟏 } 3/1=3
𝒔 𝟑
𝟑
= {𝒗 𝟐, 𝒗 𝟏} 10/2=5
𝒔 𝟒
𝟑
= ф Reject
𝒔 𝟓
𝟑
= ф Reject
𝒔 𝟕
𝟑
= ф Reject
𝒔 𝟏𝟏
𝟑
= ф Reject
min

22. l=3 (Iteration 3)
𝒗𝒋= 𝒗 𝟐
D = { 𝐯 𝟖, 𝐯 𝟔, 𝒗 𝟐}
𝑼 𝟑
= V - 𝒔 𝟐
𝟏
- 𝒗 𝟐
= ф
𝒔 𝟏
𝟒
= ф Reject
𝒔 𝟐
𝟒
= ф Reject
𝒔 𝟑
𝟒
= ф Reject
The while loop ends here
because 𝑼 𝟑
=ф
Therefore,
D = { 𝐯 𝟖, 𝐯 𝟔, 𝒗 𝟐}
𝒗 𝟏𝟏
𝒗 𝟏 𝒗 𝟐
𝒗 𝟏𝟎
𝒗 𝟓
𝒗 𝟒
𝒗 𝟕
𝒗 𝟖
𝒗 𝟗
𝒗 𝟔
𝒗 𝟑
(7)
(3)
(10)
(4)
(9)
(6)
(11)
(2)
(13)
(8)
(8)

23. Phase 2 is to check whether the minimum weighted dominating set generated in the given
in the algorithm above is secure or not.
We take a vertex 𝑣𝑖 from the remaining vertices 𝑴𝑾𝑫𝑺 and checking for its neighbours in
MWDS. For each vertex 𝑣𝑗 ∈ MWDS which is a neighbour of 𝑣𝑖 , replace 𝑣𝑗 from
MWDS with 𝑣𝑖 and check if it is a dominating set. If this process is successful for each
𝑣𝑖,then we can say that the given MWDS is a secure dominating set

24. Algorithm for checking Secure Domination
1. Input: Graph G = (V,E), Minimum weighted Dominating Set MWDS
2. Output: 1 if MWDS is secure else 0
3. 𝒐𝒗𝒆𝒓𝒂𝒍𝒍_𝒄𝒉𝒆𝒄𝒌 ∶= false.
4. for each 𝒗𝒊 ∈ 𝑴𝑾𝑫𝑺
a) 𝐓𝐢 ← ф
b)for every neighbour 𝒗𝒋 of 𝒗𝒊 , 𝒗𝒋 ∈ MWDS
i. 𝑻𝒊 ←{ MWDS {𝒗𝒋} } ∪ 𝒗𝒊
c) End
d) 𝐜𝐡𝐞𝐜𝐤 ∶= false
e) for every set 𝒎 in 𝑻𝒊
i. if Dominating (𝒎) == 𝒕𝒓𝒖𝒆 ,𝒄𝒉𝒆𝒄𝒌 ∶= true, End
ii. else continue.
f) End

25. Algorithm for checking Secure Domination(Conti.)
g) if 𝒄𝒉𝒆𝒄𝒌== true
i. 𝒐𝒗𝒆𝒓𝒂𝒍𝒍_𝒄𝒉𝒆𝒄𝒌 ∶= true; continue
h) Else
i. 𝒐𝒗𝒆𝒓𝒂𝒍𝒍_𝒄𝒉𝒆𝒄𝒌 := false, End the for loop
5. End
6. If 𝒐𝒗𝒆𝒓𝒂𝒍𝒍_𝒄𝒉𝒆𝒄𝒌 == true
a) Return 1
7. Else
a) Return 0

26. Phase 3 is to to make the minimum weighted dominating set generated in the given in the
algorithm as secure
In case in phase 2 returns 1, then the final solution will be the Minimum weighted domination set
generated by algorithm in phase 1
If the above algorithm returns 0, we need to make the minimum weighted domination set secure.
In doing so, we again make a greedy choice of choosing the vertex with minimum weight
and maximum neighbours from the remaining vertices. Then we will add that vertex to the
existing MWDS and check if its secure using algorithm 2

27. Algorithm for MSWDS
1. Input: Graph G = (V,E),MWDS
2. Output: A minimum secure weighted Dominating Set S
3. If Secure(MWDS)
a) S ← MWDS
4. Else do
a) N:= |V| - |MWDS|
b) While Secure(MWDS) ≠ true
i. For k:=1 to N
ii. Choose 𝑪 𝒌
𝑵
vertices set 𝑽′
such arg 𝒎𝒊𝒏 𝒗 𝒊Є𝑫
𝒘(𝒗 𝒊)
𝑺 𝒊
𝒍 ,𝒗𝒊∈𝑽′
iii. 𝑴𝑾𝑫𝑺 ← MWDS ∪ 𝑽′
iv. If Secure(MWDS)
i. S ← MWDS
v. Else
i. Continue.
c) End
5. End
6. Return S

28. Conclusion
 An approximation ratio of O(log n) can be seen for minimum
weighted dominating set.
 In making a weighted dominating set secure, we are choosing
vertices from the remaining vertices and adding them to the
minimum weighted dominating set . This requires where N =
|V| - |MWDS|. Next an example graph has been solved in the
Section 4.
 The algorithm presented in this report doesn’t give an optimal
solution. Instead a heuristic algorithm is chosen to get the
best possible solution for NP- Complete problem.

29. References
(1) K.S.Booth and J.H.Johnson Dominating Sets in Chordal Graph,SAIM Journal
on Computing ,11 ,191-199,1982
(2) E. J. Cock ayne, P.J.P Grobler, W. R. Crundlingh , J. Munganja and J. H. Van
Vuren Protection of a Graph,Utilities Mathematics 67, 19-32, 2005
(3) T . W. Haynes, S. T. Hedetniemi and P . J Slater , Fundamental of Domination in
Graphs, Marcel Dekker Inc. New York 1998
(4) R. G. Michael and D .S. Johnson Computers and Intractability :: A Guide to the
Theory of NP- completeness, San Francisco 1979
(5) H. B. Merouane and M. Chellai , On Secure Domination in Graph Information
Processing, Letters 786-790, 2015
(6) Ning Chen, Jie Meng, Jiawei Rong, Hong Zhu,Approximation for Dominating
Set Problem with Measure Functions,Department of Computer Science, Fudan
University P. R. China ,2003

30. THANK YOU