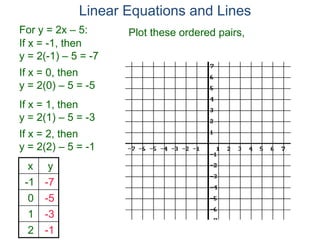
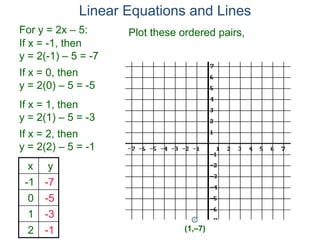
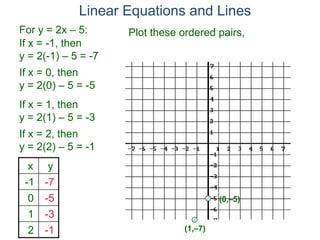
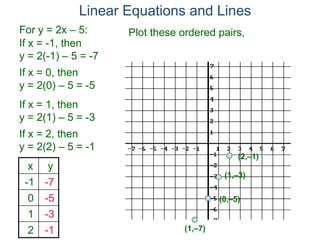
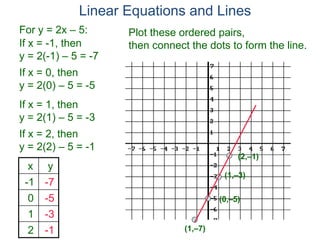
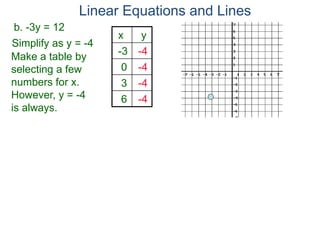
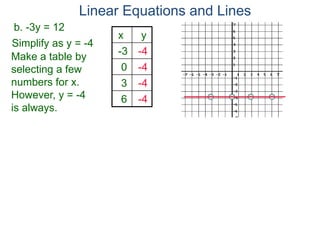
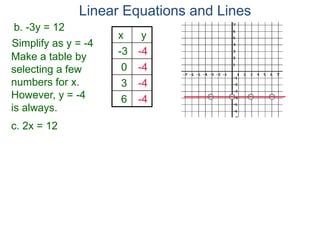
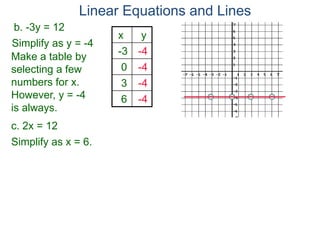
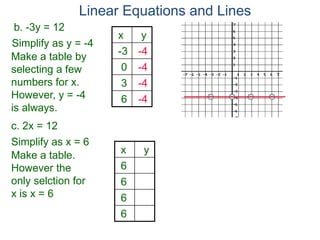
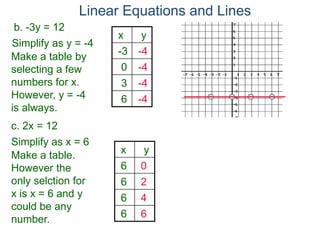
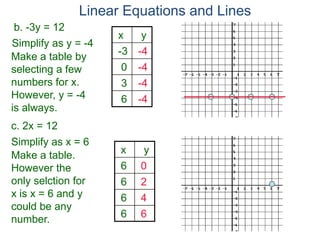
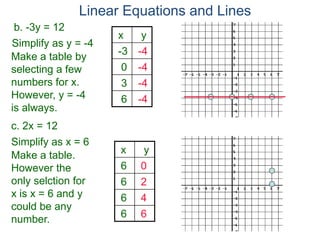
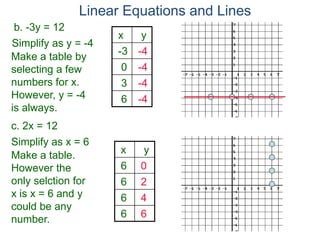
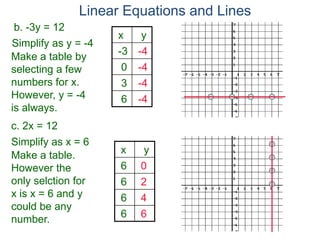
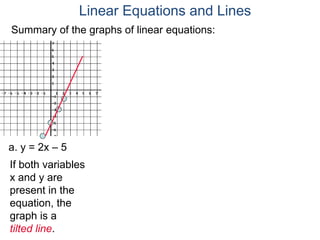
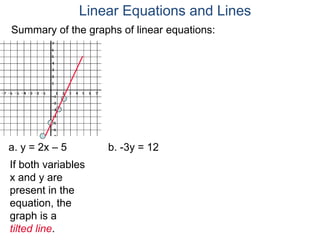
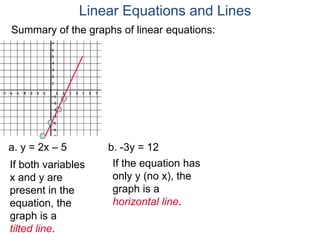
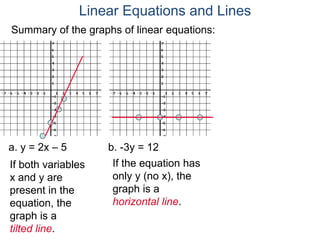
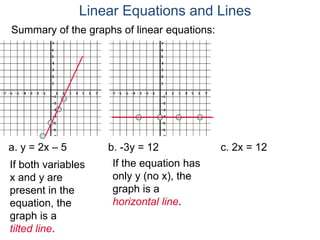
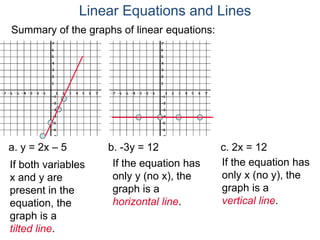
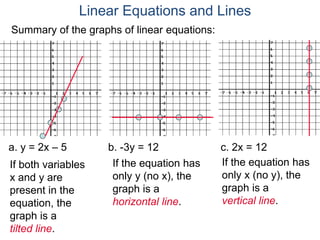
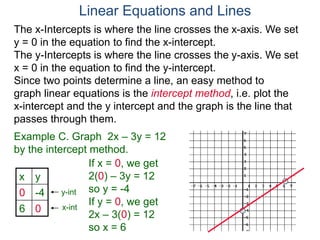
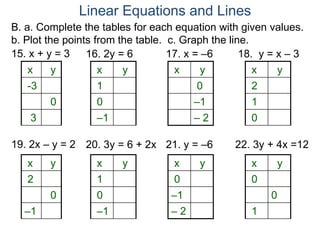
The document discusses linear equations and how to graph them. It explains that linear equations relate the x-coordinate and y-coordinate of points in a straight line. To graph a linear equation, one finds ordered pairs that satisfy the equation by choosing values for x and solving for y, then plots the points. An example demonstrates graphing the linear equation y = 2x - 5 by making a table of x and y values and plotting the line.

1. Linear Equations and Lines

2. In the rectangular coordinate system, ordered pairs (x, y)’s
correspond to locations of points.
Linear Equations and Lines

3. In the rectangular coordinate system, ordered pairs (x, y)’s
correspond to locations of points. Collections of points may be
specified by the mathematics relations between the
x-coordinate and the y coordinate.
Linear Equations and Lines

4. In the rectangular coordinate system, ordered pairs (x, y)’s
correspond to locations of points. Collections of points may be
specified by the mathematics relations between the
x-coordinate and the y coordinate. The plot of points that fit a
given relation is called the graph of that relation.
Linear Equations and Lines

5. In the rectangular coordinate system, ordered pairs (x, y)’s
correspond to locations of points. Collections of points may be
specified by the mathematics relations between the
x-coordinate and the y coordinate. The plot of points that fit a
given relation is called the graph of that relation. To make a
graph of a given mathematics relation, make a table of points
that fit the description and plot them.
Linear Equations and Lines

6. Example A. Graph the points (x, y) where x = –4
In the rectangular coordinate system, ordered pairs (x, y)’s
correspond to locations of points. Collections of points may be
specified by the mathematics relations between the
x-coordinate and the y coordinate. The plot of points that fit a
given relation is called the graph of that relation. To make a
graph of a given mathematics relation, make a table of points
that fit the description and plot them.
Linear Equations and Lines

7. Example A. Graph the points (x, y) where x = –4
(y can be anything).
In the rectangular coordinate system, ordered pairs (x, y)’s
correspond to locations of points. Collections of points may be
specified by the mathematics relations between the
x-coordinate and the y coordinate. The plot of points that fit a
given relation is called the graph of that relation. To make a
graph of a given mathematics relation, make a table of points
that fit the description and plot them.
Linear Equations and Lines

8. Example A. Graph the points (x, y) where x = –4
(y can be anything).
Make a table of
ordered pairs of
points that fit the
description
x = –4.
In the rectangular coordinate system, ordered pairs (x, y)’s
correspond to locations of points. Collections of points may be
specified by the mathematics relations between the
x-coordinate and the y coordinate. The plot of points that fit a
given relation is called the graph of that relation. To make a
graph of a given mathematics relation, make a table of points
that fit the description and plot them.
Linear Equations and Lines

9. Linear Equations and Lines
Example A. Graph the points (x, y) where x = –4
(y can be anything).
x y
–4
–4
–4
–4
Make a table of
ordered pairs of
points that fit the
description
x = –4.
In the rectangular coordinate system, ordered pairs (x, y)’s
correspond to locations of points. Collections of points may be
specified by the mathematics relations between the
x-coordinate and the y coordinate. The plot of points that fit a
given relation is called the graph of that relation. To make a
graph of a given mathematics relation, make a table of points
that fit the description and plot them.
Linear Equations and Lines

10. Example A. Graph the points (x, y) where x = –4
(y can be anything).
x y
–4 0
–4
–4
–4
Make a table of
ordered pairs of
points that fit the
description
x = –4.
In the rectangular coordinate system, ordered pairs (x, y)’s
correspond to locations of points. Collections of points may be
specified by the mathematics relations between the
x-coordinate and the y coordinate. The plot of points that fit a
given relation is called the graph of that relation. To make a
graph of a given mathematics relation, make a table of points
that fit the description and plot them.
Linear Equations and Lines

11. Example A. Graph the points (x, y) where x = –4
(y can be anything).
x y
–4 0
–4 2
–4
–4
Make a table of
ordered pairs of
points that fit the
description
x = –4.
In the rectangular coordinate system, ordered pairs (x, y)’s
correspond to locations of points. Collections of points may be
specified by the mathematics relations between the
x-coordinate and the y coordinate. The plot of points that fit a
given relation is called the graph of that relation. To make a
graph of a given mathematics relation, make a table of points
that fit the description and plot them.
Linear Equations and Lines

12. Example A. Graph the points (x, y) where x = –4
(y can be anything).
x y
–4 0
–4 2
–4 4
–4 6
Make a table of
ordered pairs of
points that fit the
description
x = –4.
In the rectangular coordinate system, ordered pairs (x, y)’s
correspond to locations of points. Collections of points may be
specified by the mathematics relations between the
x-coordinate and the y coordinate. The plot of points that fit a
given relation is called the graph of that relation. To make a
graph of a given mathematics relation, make a table of points
that fit the description and plot them.
Linear Equations and Lines

13. Example A. Graph the points (x, y) where x = –4
(y can be anything).
x y
–4 0
–4 2
–4 4
–4 6
Graph of x = –4
Make a table of
ordered pairs of
points that fit the
description
x = –4.
In the rectangular coordinate system, ordered pairs (x, y)’s
correspond to locations of points. Collections of points may be
specified by the mathematics relations between the
x-coordinate and the y coordinate. The plot of points that fit a
given relation is called the graph of that relation. To make a
graph of a given mathematics relation, make a table of points
that fit the description and plot them.
Linear Equations and Lines

14. First degree equation in the variables x and y are equations
that may be put into the form Ax + By = C where A, B, C are
numbers.
Linear Equations and Lines

15. First degree equation in the variables x and y are equations
that may be put into the form Ax + By = C where A, B, C are
numbers. First degree equations are the same as linear
equations.
Linear Equations and Lines

16. First degree equation in the variables x and y are equations
that may be put into the form Ax + By = C where A, B, C are
numbers. First degree equations are the same as linear
equations. They are called linear because their graphs are
straight lines.
Linear Equations and Lines

17. First degree equation in the variables x and y are equations
that may be put into the form Ax + By = C where A, B, C are
numbers. First degree equations are the same as linear
equations. They are called linear because their graphs are
straight lines. To graph a linear equation, find a few ordered
pairs that fit the equation.
Linear Equations and Lines

18. First degree equation in the variables x and y are equations
that may be put into the form Ax + By = C where A, B, C are
numbers. First degree equations are the same as linear
equations. They are called linear because their graphs are
straight lines. To graph a linear equation, find a few ordered
pairs that fit the equation.
Example B.
Graph the following linear equations.
a. y = 2x – 5
Linear Equations and Lines

19. First degree equation in the variables x and y are equations
that may be put into the form Ax + By = C where A, B, C are
numbers. First degree equations are the same as linear
equations. They are called linear because their graphs are
straight lines. To graph a linear equation, find a few ordered
pairs that fit the equation. To find one such ordered pair, assign
a value to x, plug it into the equation and solve for the y
(or assign a value to y and solve for the x).
Example B.
Graph the following linear equations.
a. y = 2x – 5
Linear Equations and Lines

20. First degree equation in the variables x and y are equations
that may be put into the form Ax + By = C where A, B, C are
numbers. First degree equations are the same as linear
equations. They are called linear because their graphs are
straight lines. To graph a linear equation, find a few ordered
pairs that fit the equation. To find one such ordered pair, assign
a value to x, plug it into the equation and solve for the y
(or assign a value to y and solve for the x).
Example B.
Graph the following linear equations.
a. y = 2x – 5
Make a table by selecting a few numbers for x.
Linear Equations and Lines

21. First degree equation in the variables x and y are equations
that may be put into the form Ax + By = C where A, B, C are
numbers. First degree equations are the same as linear
equations. They are called linear because their graphs are
straight lines. To graph a linear equation, find a few ordered
pairs that fit the equation. To find one such ordered pair, assign
a value to x, plug it into the equation and solve for the y
(or assign a value to y and solve for the x).
For graphing lines, find at least two ordered pairs.
Example B.
Graph the following linear equations.
a. y = 2x – 5
Make a table by selecting a few numbers for x.
Linear Equations and Lines

22. First degree equation in the variables x and y are equations
that may be put into the form Ax + By = C where A, B, C are
numbers. First degree equations are the same as linear
equations. They are called linear because their graphs are
straight lines. To graph a linear equation, find a few ordered
pairs that fit the equation. To find one such ordered pair, assign
a value to x, plug it into the equation and solve for the y
(or assign a value to y and solve for the x).
For graphing lines, find at least two ordered pairs.
Example B.
Graph the following linear equations.
a. y = 2x – 5
Make a table by selecting a few numbers for x.
For easy calculation let’s select x = -1, 0, 1, and 2.
Linear Equations and Lines

23. First degree equation in the variables x and y are equations
that may be put into the form Ax + By = C where A, B, C are
numbers. First degree equations are the same as linear
equations. They are called linear because their graphs are
straight lines. To graph a linear equation, find a few ordered
pairs that fit the equation. To find one such ordered pair, assign
a value to x, plug it into the equation and solve for the y
(or assign a value to y and solve for the x).
For graphing lines, find at least two ordered pairs.
Example B.
Graph the following linear equations.
a. y = 2x – 5
Make a table by selecting a few numbers for x.
For easy calculation let’s select x = -1, 0, 1, and 2.
Plug these value into x and solve for y, one at a time,
to obtain four ordered pair as shown below.
Linear Equations and Lines

24. For y = 2x – 5:
x y
-1
0
1
2
Linear Equations and Lines

25. For y = 2x – 5:
x y
-1
0
1
2
If x = -1, then
y = 2(-1) – 5
Linear Equations and Lines

26. For y = 2x – 5:
x y
-1 -7
0
1
2
If x = -1, then
y = 2(-1) – 5 = -7
Linear Equations and Lines

27. For y = 2x – 5:
x y
-1 -7
0 -5
1
2
If x = -1, then
y = 2(-1) – 5 = -7
If x = 0, then
y = 2(0) – 5
Linear Equations and Lines

28. For y = 2x – 5:
x y
-1 -7
0 -5
1
2
If x = -1, then
y = 2(-1) – 5 = -7
If x = 0, then
y = 2(0) – 5 = -5
Linear Equations and Lines

29. For y = 2x – 5:
x y
-1 -7
0 -5
1 -3
2 -1
If x = -1, then
y = 2(-1) – 5 = -7
If x = 0, then
y = 2(0) – 5 = -5
If x = 1, then
y = 2(1) – 5 = -3
If x = 2, then
y = 2(2) – 5 = -1
Linear Equations and Lines

30. For y = 2x – 5:
x y
-1 -7
0 -5
1 -3
2 -1
If x = -1, then
y = 2(-1) – 5 = -7
If x = 0, then
y = 2(0) – 5 = -5
If x = 1, then
y = 2(1) – 5 = -3
If x = 2, then
y = 2(2) – 5 = -1
Linear Equations and Lines
Plot these ordered pairs,

31. For y = 2x – 5:
x y
-1 -7
0 -5
1 -3
2 -1
If x = -1, then
y = 2(-1) – 5 = -7
If x = 0, then
y = 2(0) – 5 = -5
If x = 1, then
y = 2(1) – 5 = -3
If x = 2, then
y = 2(2) – 5 = -1
Linear Equations and Lines
Plot these ordered pairs,
(1,–7)

32. For y = 2x – 5:
x y
-1 -7
0 -5
1 -3
2 -1
If x = -1, then
y = 2(-1) – 5 = -7
If x = 0, then
y = 2(0) – 5 = -5
If x = 1, then
y = 2(1) – 5 = -3
If x = 2, then
y = 2(2) – 5 = -1
Linear Equations and Lines
Plot these ordered pairs,
(1,–7)
(0,–5)

33. For y = 2x – 5:
x y
-1 -7
0 -5
1 -3
2 -1
If x = -1, then
y = 2(-1) – 5 = -7
If x = 0, then
y = 2(0) – 5 = -5
If x = 1, then
y = 2(1) – 5 = -3
If x = 2, then
y = 2(2) – 5 = -1
Linear Equations and Lines
(1,–7)
(0,–5)
(1,–3)
(2,–1)
Plot these ordered pairs,

34. For y = 2x – 5:
x y
-1 -7
0 -5
1 -3
2 -1
If x = -1, then
y = 2(-1) – 5 = -7
If x = 0, then
y = 2(0) – 5 = -5
If x = 1, then
y = 2(1) – 5 = -3
If x = 2, then
y = 2(2) – 5 = -1
Linear Equations and Lines
(1,–7)
(0,–5)
(1,–3)
(2,–1)
Plot these ordered pairs,
then connect the dots to form the line.

35. b. -3y = 12
Linear Equations and Lines

36. b. -3y = 12
Simplify as y = -4
Make a table by
selecting a few
numbers for x.
Linear Equations and Lines

37. b. -3y = 12
Simplify as y = -4
Make a table by
selecting a few
numbers for x.
x y
-3
0
3
6
Linear Equations and Lines

38. b. -3y = 12
Simplify as y = -4
Make a table by
selecting a few
numbers for x.
However, y = -4
is always.
x y
-3 -4
0 -4
3 -4
6 -4
Linear Equations and Lines

39. b. -3y = 12
Simplify as y = -4
Make a table by
selecting a few
numbers for x.
However, y = -4
is always.
x y
-3 -4
0 -4
3 -4
6 -4
Linear Equations and Lines

40. b. -3y = 12
Simplify as y = -4
Make a table by
selecting a few
numbers for x.
However, y = -4
is always.
x y
-3 -4
0 -4
3 -4
6 -4
Linear Equations and Lines

41. b. -3y = 12
Simplify as y = -4
Make a table by
selecting a few
numbers for x.
However, y = -4
is always.
x y
-3 -4
0 -4
3 -4
6 -4
Linear Equations and Lines

42. b. -3y = 12
Simplify as y = -4
c. 2x = 12
Make a table by
selecting a few
numbers for x.
However, y = -4
is always.
x y
-3 -4
0 -4
3 -4
6 -4
Linear Equations and Lines

43. b. -3y = 12
Simplify as y = -4
c. 2x = 12
Make a table by
selecting a few
numbers for x.
However, y = -4
is always.
x y
-3 -4
0 -4
3 -4
6 -4
Simplify as x = 6.
Linear Equations and Lines

44. b. -3y = 12
Simplify as y = -4
c. 2x = 12
Make a table by
selecting a few
numbers for x.
However, y = -4
is always.
x y
-3 -4
0 -4
3 -4
6 -4
Simplify as x = 6
Make a table.
However the
only selction for
x is x = 6
Linear Equations and Lines

45. b. -3y = 12
Simplify as y = -4
c. 2x = 12
Make a table by
selecting a few
numbers for x.
However, y = -4
is always.
x y
-3 -4
0 -4
3 -4
6 -4
Simplify as x = 6
Make a table.
However the
only selction for
x is x = 6
x y
6
6
6
6
Linear Equations and Lines

46. b. -3y = 12
Simplify as y = -4
c. 2x = 12
Make a table by
selecting a few
numbers for x.
However, y = -4
is always.
x y
-3 -4
0 -4
3 -4
6 -4
Simplify as x = 6
Make a table.
However the
only selction for
x is x = 6 and y
could be any
number.
x y
6 0
6 2
6 4
6 6
Linear Equations and Lines

47. b. -3y = 12
Simplify as y = -4
c. 2x = 12
Make a table by
selecting a few
numbers for x.
However, y = -4
is always.
x y
-3 -4
0 -4
3 -4
6 -4
Simplify as x = 6
Make a table.
However the
only selction for
x is x = 6 and y
could be any
number.
x y
6 0
6 2
6 4
6 6
Linear Equations and Lines

48. b. -3y = 12
Simplify as y = -4
c. 2x = 12
Make a table by
selecting a few
numbers for x.
However, y = -4
is always.
x y
-3 -4
0 -4
3 -4
6 -4
Simplify as x = 6
Make a table.
However the
only selction for
x is x = 6 and y
could be any
number.
x y
6 0
6 2
6 4
6 6
Linear Equations and Lines

49. b. -3y = 12
Simplify as y = -4
c. 2x = 12
Make a table by
selecting a few
numbers for x.
However, y = -4
is always.
x y
-3 -4
0 -4
3 -4
6 -4
Simplify as x = 6
Make a table.
However the
only selction for
x is x = 6 and y
could be any
number.
x y
6 0
6 2
6 4
6 6
Linear Equations and Lines

50. b. -3y = 12
Simplify as y = -4
c. 2x = 12
Make a table by
selecting a few
numbers for x.
However, y = -4
is always.
x y
-3 -4
0 -4
3 -4
6 -4
Simplify as x = 6
Make a table.
However the
only selction for
x is x = 6 and y
could be any
number.
x y
6 0
6 2
6 4
6 6
Linear Equations and Lines

51. Summary of the graphs of linear equations:
Linear Equations and Lines

52. a. y = 2x – 5
Summary of the graphs of linear equations:
Linear Equations and Lines

53. a. y = 2x – 5
If both variables
x and y are
present in the
equation, the
graph is a
tilted line.
Summary of the graphs of linear equations:
Linear Equations and Lines

54. a. y = 2x – 5
If both variables
x and y are
present in the
equation, the
graph is a
tilted line.
Summary of the graphs of linear equations:
Linear Equations and Lines

55. a. y = 2x – 5 b. -3y = 12
If both variables
x and y are
present in the
equation, the
graph is a
tilted line.
Summary of the graphs of linear equations:
Linear Equations and Lines

56. a. y = 2x – 5 b. -3y = 12
If both variables
x and y are
present in the
equation, the
graph is a
tilted line.
If the equation has
only y (no x), the
graph is a
horizontal line.
Summary of the graphs of linear equations:
Linear Equations and Lines

57. a. y = 2x – 5 b. -3y = 12
If both variables
x and y are
present in the
equation, the
graph is a
tilted line.
If the equation has
only y (no x), the
graph is a
horizontal line.
Summary of the graphs of linear equations:
Linear Equations and Lines

58. a. y = 2x – 5 b. -3y = 12 c. 2x = 12
If both variables
x and y are
present in the
equation, the
graph is a
tilted line.
If the equation has
only y (no x), the
graph is a
horizontal line.
Summary of the graphs of linear equations:
Linear Equations and Lines

59. a. y = 2x – 5 b. -3y = 12 c. 2x = 12
If both variables
x and y are
present in the
equation, the
graph is a
tilted line.
If the equation has
only y (no x), the
graph is a
horizontal line.
Summary of the graphs of linear equations:
If the equation has
only x (no y), the
graph is a
vertical line.
Linear Equations and Lines

60. a. y = 2x – 5 b. -3y = 12 c. 2x = 12
If both variables
x and y are
present in the
equation, the
graph is a
tilted line.
If the equation has
only y (no x), the
graph is a
horizontal line.
Summary of the graphs of linear equations:
If the equation has
only x (no y), the
graph is a
vertical line.
Linear Equations and Lines

61. The x-Intercepts is where the line crosses the x-axis;
Linear Equations and Lines

62. The x-Intercepts is where the line crosses the x-axis. We set
y = 0 in the equation to find the x-intercept.
Linear Equations and Lines

63. The x-Intercepts is where the line crosses the x-axis. We set
y = 0 in the equation to find the x-intercept.
The y-Intercepts is where the line crosses the y-axis;
Linear Equations and Lines

64. The x-Intercepts is where the line crosses the x-axis. We set
y = 0 in the equation to find the x-intercept.
The y-Intercepts is where the line crosses the y-axis. We set
x = 0 in the equation to find the y-intercept.
Linear Equations and Lines

65. The x-Intercepts is where the line crosses the x-axis. We set
y = 0 in the equation to find the x-intercept.
The y-Intercepts is where the line crosses the y-axis. We set
x = 0 in the equation to find the y-intercept.
Since two points determine a line, an easy method to
graph linear equations is the intercept method,
Linear Equations and Lines

66. The x-Intercepts is where the line crosses the x-axis. We set
y = 0 in the equation to find the x-intercept.
The y-Intercepts is where the line crosses the y-axis. We set
x = 0 in the equation to find the y-intercept.
Since two points determine a line, an easy method to
graph linear equations is the intercept method, i.e. plot the
x-intercept and the y intercept and the graph is the line that
passes through them.
Linear Equations and Lines

67. The x-Intercepts is where the line crosses the x-axis. We set
y = 0 in the equation to find the x-intercept.
The y-Intercepts is where the line crosses the y-axis. We set
x = 0 in the equation to find the y-intercept.
Example C. Graph 2x – 3y = 12
by the intercept method.
Since two points determine a line, an easy method to
graph linear equations is the intercept method, i.e. plot the
x-intercept and the y intercept and the graph is the line that
passes through them.
Linear Equations and Lines

68. x y
0
0
The x-Intercepts is where the line crosses the x-axis. We set
y = 0 in the equation to find the x-intercept.
The y-Intercepts is where the line crosses the y-axis. We set
x = 0 in the equation to find the y-intercept.
y-int
x-int
Example C. Graph 2x – 3y = 12
by the intercept method.
Since two points determine a line, an easy method to
graph linear equations is the intercept method, i.e. plot the
x-intercept and the y intercept and the graph is the line that
passes through them.
Linear Equations and Lines

69. x y
0
0
The x-Intercepts is where the line crosses the x-axis. We set
y = 0 in the equation to find the x-intercept.
The y-Intercepts is where the line crosses the y-axis. We set
x = 0 in the equation to find the y-intercept.
y-int
x-int
Example C. Graph 2x – 3y = 12
by the intercept method.
Since two points determine a line, an easy method to
graph linear equations is the intercept method, i.e. plot the
x-intercept and the y intercept and the graph is the line that
passes through them.
If x = 0, we get
2(0) – 3y = 12
Linear Equations and Lines

70. x y
0 -4
0
The x-Intercepts is where the line crosses the x-axis. We set
y = 0 in the equation to find the x-intercept.
The y-Intercepts is where the line crosses the y-axis. We set
x = 0 in the equation to find the y-intercept.
y-int
x-int
Example C. Graph 2x – 3y = 12
by the intercept method.
Since two points determine a line, an easy method to
graph linear equations is the intercept method, i.e. plot the
x-intercept and the y intercept and the graph is the line that
passes through them.
If x = 0, we get
2(0) – 3y = 12
so y = -4
Linear Equations and Lines

71. x y
0 -4
0
The x-Intercepts is where the line crosses the x-axis. We set
y = 0 in the equation to find the x-intercept.
The y-Intercepts is where the line crosses the y-axis. We set
x = 0 in the equation to find the y-intercept.
y-int
x-int
Example C. Graph 2x – 3y = 12
by the intercept method.
Since two points determine a line, an easy method to
graph linear equations is the intercept method, i.e. plot the
x-intercept and the y intercept and the graph is the line that
passes through them.
If x = 0, we get
2(0) – 3y = 12
so y = -4
If y = 0, we get
2x – 3(0) = 12
Linear Equations and Lines

72. x y
0 -4
6 0
The x-Intercepts is where the line crosses the x-axis. We set
y = 0 in the equation to find the x-intercept.
The y-Intercepts is where the line crosses the y-axis. We set
x = 0 in the equation to find the y-intercept.
y-int
x-int
Example C. Graph 2x – 3y = 12
by the intercept method.
Since two points determine a line, an easy method to
graph linear equations is the intercept method, i.e. plot the
x-intercept and the y intercept and the graph is the line that
passes through them.
If x = 0, we get
2(0) – 3y = 12
so y = -4
If y = 0, we get
2x – 3(0) = 12
so x = 6
Linear Equations and Lines

73. x y
0 -4
6 0
The x-Intercepts is where the line crosses the x-axis. We set
y = 0 in the equation to find the x-intercept.
The y-Intercepts is where the line crosses the y-axis. We set
x = 0 in the equation to find the y-intercept.
y-int
x-int
Example C. Graph 2x – 3y = 12
by the intercept method.
Since two points determine a line, an easy method to
graph linear equations is the intercept method, i.e. plot the
x-intercept and the y intercept and the graph is the line that
passes through them.
If x = 0, we get
2(0) – 3y = 12
so y = -4
If y = 0, we get
2x – 3(0) = 12
so x = 6
Linear Equations and Lines

74. x y
0 -4
6 0
The x-Intercepts is where the line crosses the x-axis. We set
y = 0 in the equation to find the x-intercept.
The y-Intercepts is where the line crosses the y-axis. We set
x = 0 in the equation to find the y-intercept.
y-int
x-int
Example C. Graph 2x – 3y = 12
by the intercept method.
Since two points determine a line, an easy method to
graph linear equations is the intercept method, i.e. plot the
x-intercept and the y intercept and the graph is the line that
passes through them.
If x = 0, we get
2(0) – 3y = 12
so y = -4
If y = 0, we get
2x – 3(0) = 12
so x = 6
Linear Equations and Lines

75. x y
0 -4
6 0
The x-Intercepts is where the line crosses the x-axis. We set
y = 0 in the equation to find the x-intercept.
The y-Intercepts is where the line crosses the y-axis. We set
x = 0 in the equation to find the y-intercept.
y-int
x-int
Example C. Graph 2x – 3y = 12
by the intercept method.
Since two points determine a line, an easy method to
graph linear equations is the intercept method, i.e. plot the
x-intercept and the y intercept and the graph is the line that
passes through them.
If x = 0, we get
2(0) – 3y = 12
so y = -4
If y = 0, we get
2x – 3(0) = 12
so x = 6
Linear Equations and Lines

76. Exercise. A. Solve the indicated variable for each equation with
the given assigned value.
1. x + y = 3 and x = –1, find y.
2. x – y = 3 and y = –1, find x.
3. 2x = 6 and y = –1, find x.
4. –y = 3 and x = 2, find y.
5. 2y = 3 – x and x = –2 , find y.
6. y = –x + 4 and x = –4, find y.
7. 2x – 3y = 1 and y = 3, find x.
8. 2x = 6 – 2y and y = –2, find x.
9. 3y – 2 = 3x and x = 2, find y.
10. 2x + 3y = 3 and x = 0, find y.
11. 2x + 3y = 3 and y = 0, find x.
12. 3x – 4y = 12 and x = 0, find y.
13. 3x – 4y = 12 and y = 0, find x.
14. 6 = 3x – 4y and y = –3, find x.
Linear Equations and Lines

77. B. a. Complete the tables for each equation with given values.
b. Plot the points from the table. c. Graph the line.
15. x + y = 3 16. 2y = 6
x y
-3
0
3
x y
1
0
–1
17. x = –6
x y
0
–1
– 2
18. y = x – 3
x y
2
1
0
19. 2x – y = 2 20. 3y = 6 + 2x
x y
2
0
–1
x y
1
0
–1
21. y = –6
x y
0
–1
– 2
22. 3y + 4x =12
x y
0
0
1
Linear Equations and Lines

78. C. Make a table for each equation with at least 3 ordered pairs.
(remember that you get to select one entry in each row as
shown in the tables above) then graph the line.
23. x – y = 3 24. 2x = 6 25. –y – 7= 0
26. 0 = 8 – 2x 27. y = –x + 4 28. 2x – 3 = 6
29. 2x = 6 – 2y 30. 4y – 12 = 3x 31. 2x + 3y = 3
32. –6 = 3x – 2y 33.
35. For problems 29, 30, 31 and 32, use the
intercept-tables as shown to graph the lines.
x y
0
0
intercept-table
36. Why can’t we use the above intercept method
to graph the lines for problems 25, 26 or 33?
37. By inspection identify which equations give
horizontal lines, which give vertical lines and
which give tilted lines.
3x = 4y 34. 5x + 2y = –10
Linear Equations and Lines