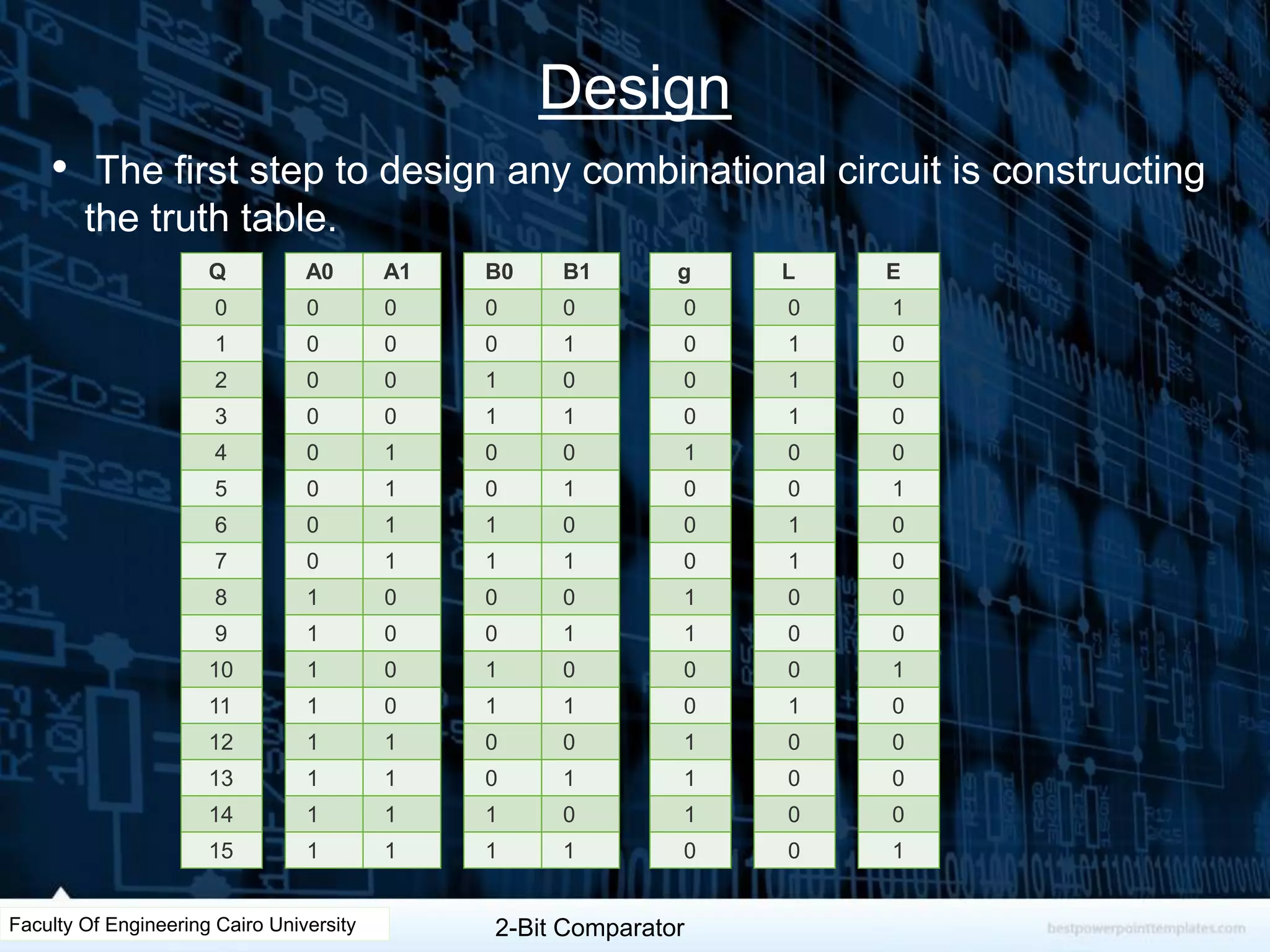
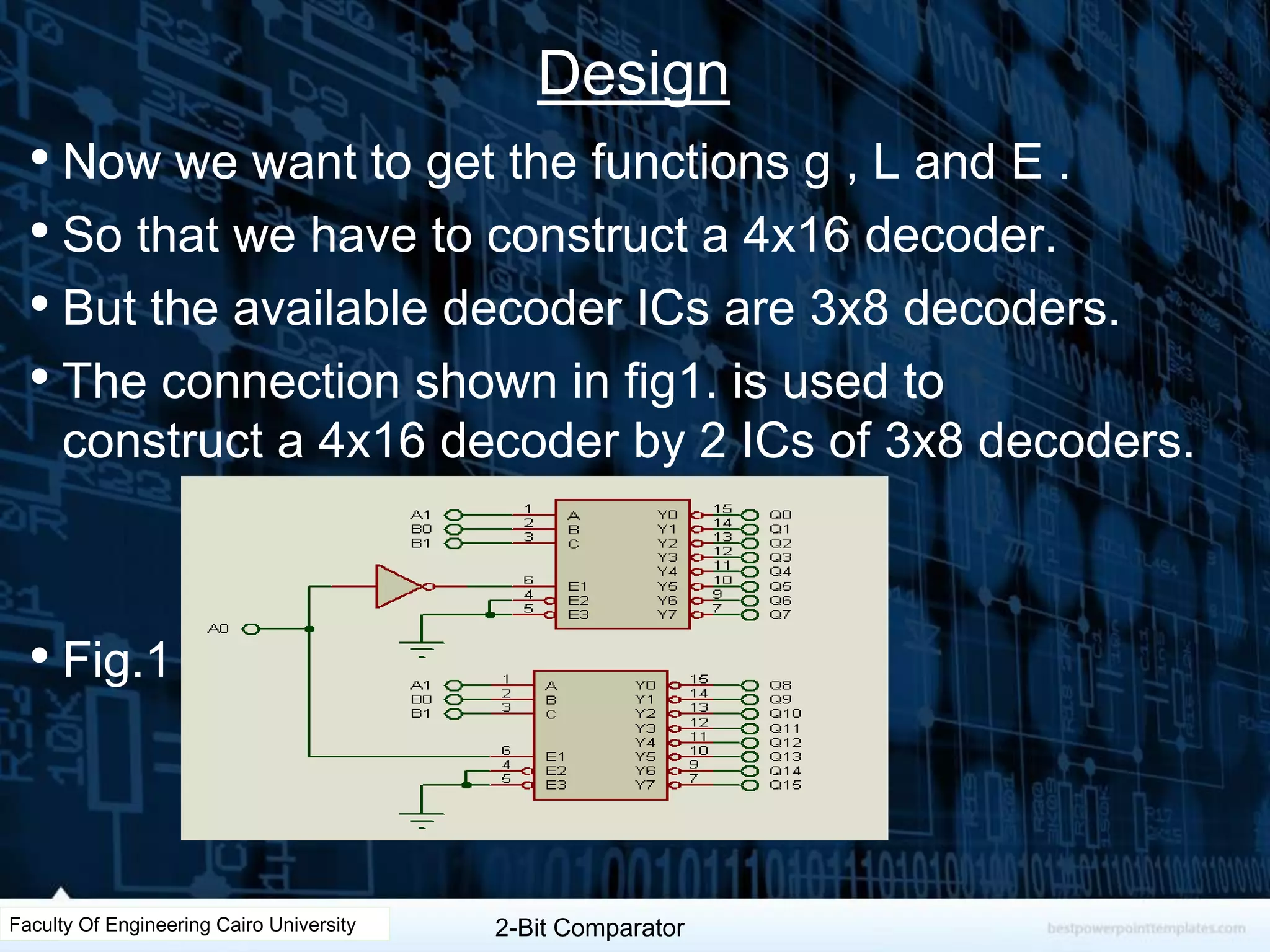
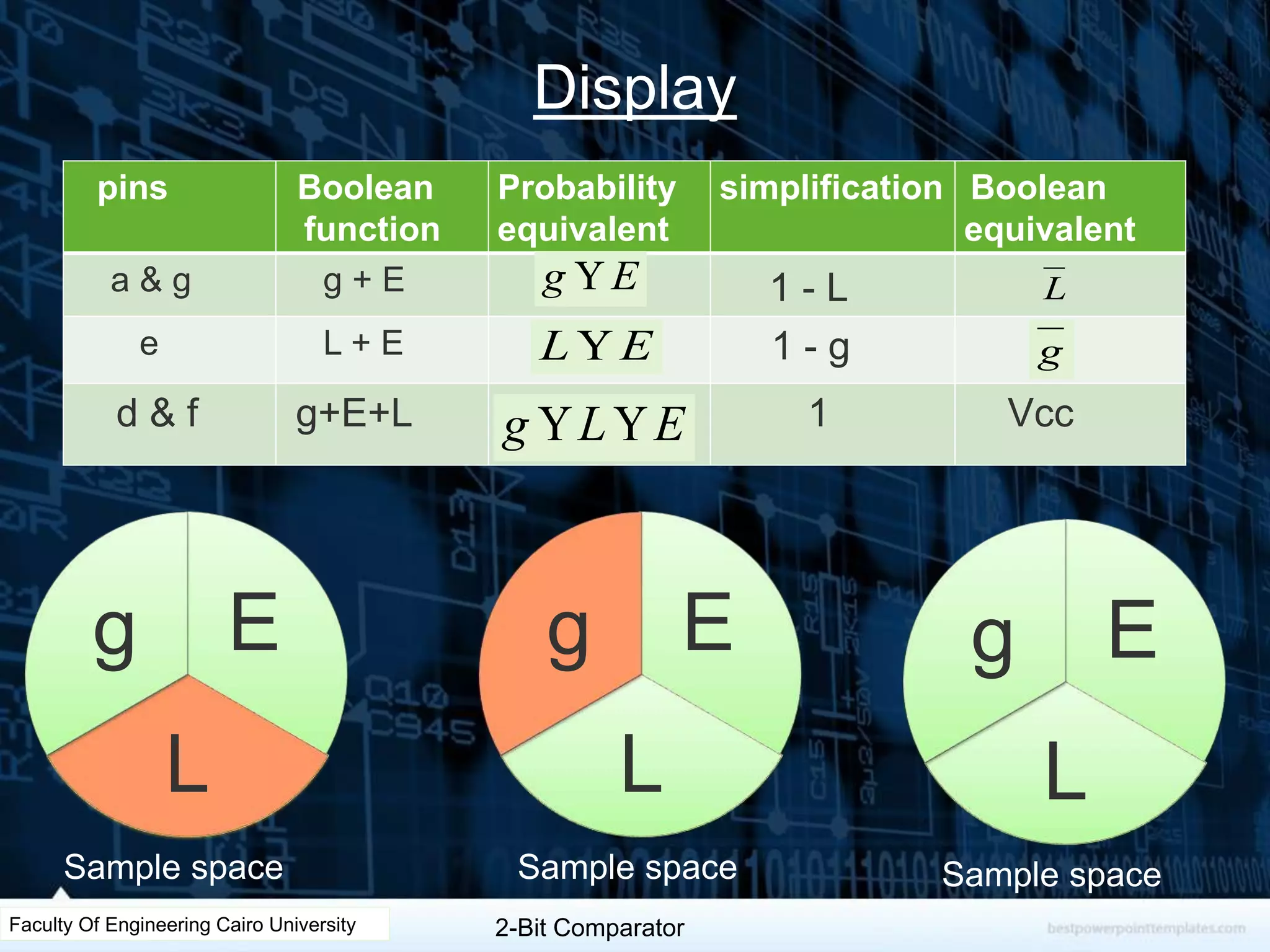
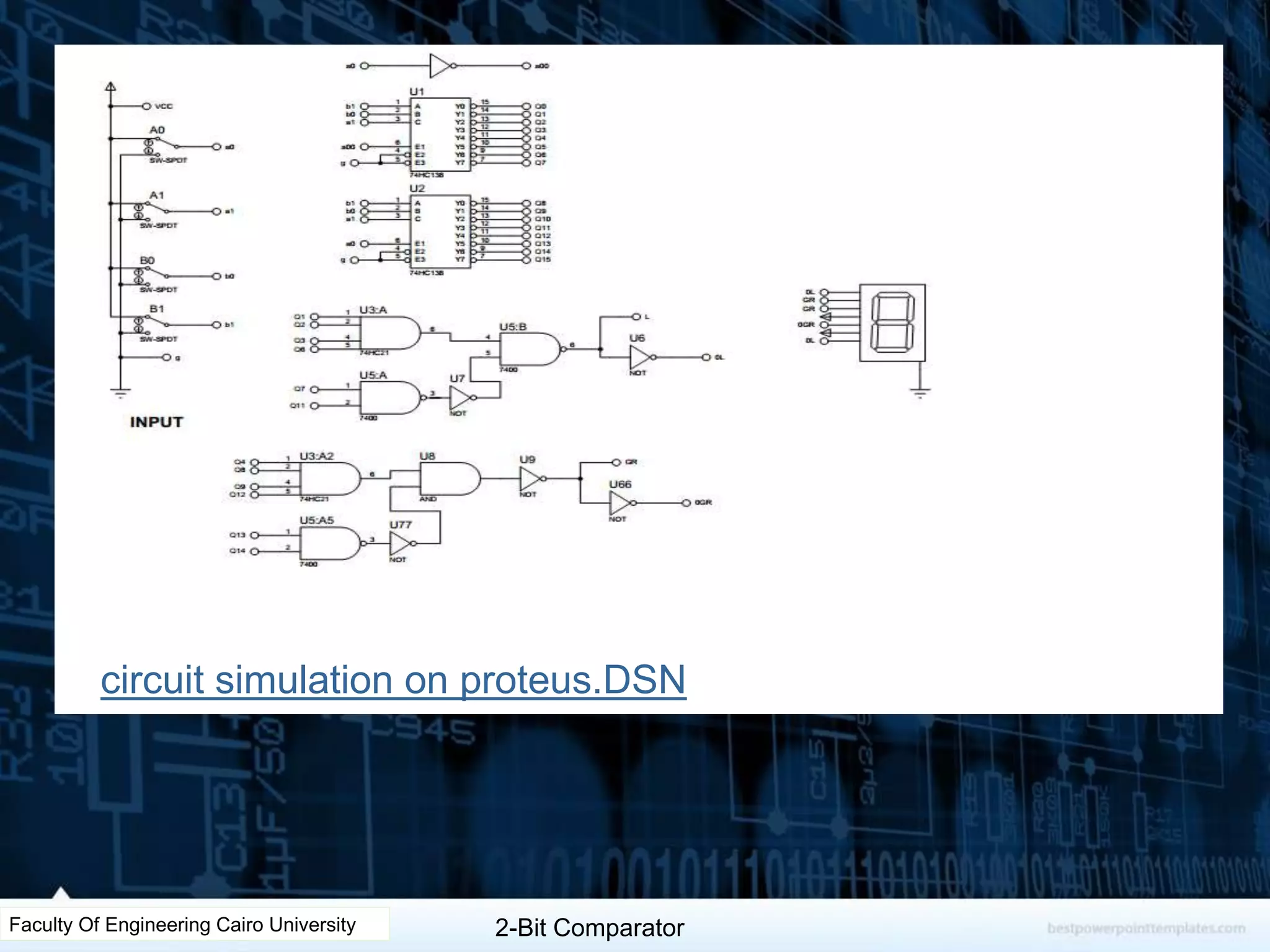
The document describes the design of a 2-bit comparator circuit. It includes constructing a truth table, minimizing the design using two 3x8 decoders as a 4x16 decoder, implementing the output functions G, L, and E using NAND gates, and displaying the output on a 7-segment display by simplifying the logic. The design was tested successfully through Proteus simulation software.

1. 2-Bit Comparator
Introduced to : DR / Mohammad Mostafa
Prepared by : Islam Adel Ataya

2. Introduction
•In this report it is clearly illustrated how to
design a 2-bit comparator circuit.
•It is also reported how we simplified the
design to use the least number of ICs.
• Design had been successfully tested by
proteus simulation software.
•The result is displayed on a 7- segment.
Faculty Of Engineering Cairo University 2-Bit Comparator

3. Problem Declaration
• It is desired to design and implement a logic
circuit that accepts two numbers each has two
bits A0 A1 & B0 B1 and compare between them.
• If A < B Print g (for greater).
• If A > B Print L (for lower).
• If A = B Print E (for equal).
• The output should be displayed on a 7- segment.
Faculty Of Engineering Cairo University 2-Bit Comparator

4. Design
• The first step to design any combinational circuit is constructing
the truth table.
A0 A1
0 0
0 0
0 0
0 0
0 1
0 1
0 1
0 1
1 0
1 0
1 0
1 0
1 1
1 1
1 1
1 1
B0 B1
0 0
0 1
1 0
1 1
0 0
0 1
1 0
1 1
0 0
0 1
1 0
1 1
0 0
0 1
1 0
1 1
g
0
0
0
0
1
0
0
0
1
1
0
0
1
1
1
0
L
0
1
1
1
0
0
1
1
0
0
0
1
0
0
0
0
E
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
Q
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Faculty Of Engineering Cairo University 2-Bit Comparator

5. Design
• Now we want to get the functions g , L and E .
• So that we have to construct a 4x16 decoder.
• But the available decoder ICs are 3x8 decoders.
• The connection shown in fig1. is used to
construct a 4x16 decoder by 2 ICs of 3x8 decoders.
• Fig.1
Faculty Of Engineering Cairo University 2-Bit Comparator

6. Design
• Minimum term algorithm is used to represent the
desired logic functions designed in the truth table.
• g = Q4 + Q8 + Q9 + Q12 + Q13 + Q14.
• L = Q1 +Q2 + Q3 + Q6 +Q7 + Q11
• E = Q0 + Q5 + Q10 + Q15
• To implement those functions the decoder output
corresponding to every functions must be applied to OR
gates.
Faculty Of Engineering Cairo University 2-Bit Comparator

7. Design
• But we should take in consideration that the outputs of
the decoder are reversed .
• DE Morgan theorem is used to solve this problem .
• Now we can implement g , L &E by applying the corresponding
decoder output of each function to NAND gates .
BABAF 
15.10.5.0
11.7.6.3.2.1
14.13.12.9.8.4
QQQQE
QQQQQQL
QQQQQQg



Faculty Of Engineering Cairo University 2-Bit Comparator

8. Display
• A 7-segment is used for displaying the result.
• The following table shows events at which every
segment should light up.
• According to this table every segment should be connected to
an OR gate that collects its corresponding events.
• OR gates are not available , so that we have to use NOR
gates in addition to not gates .
segment A B C D E F G
events G
E
g g L
G
E
L
E
L
G
E
G
E
Faculty Of Engineering Cairo University 2-Bit Comparator

9. Display
• Instead of this ,a simplification of special kind can limit the
usage of gates.
• Let us consider that we are making a random experiment by
inserting a random values of A0A1 & B0B1.
• The output of the experiment is a signal g or L or E.
• As shown in the figure sample space consists of three
independent events , in another word there is no
intersection between any two events.
• This property is very useful as a simple
simplification can be done using probability
theorem and then we can convert the result into
boolean expression.
E
L
g
Sample space
Faculty Of Engineering Cairo University 2-Bit Comparator

10. Display
pins Boolean
function
Probability
equivalent
simplification Boolean
equivalent
a & g g + E 1 - L
e L + E 1 - g
d & f g+E+L 1 Vcc
Eg 
E
L
g
Sample space
L
EL  g
ELg 
E
L
g
Sample space
E
L
g
Sample space
Faculty Of Engineering Cairo University 2-Bit Comparator

11. Display
• The following table shows the final 7-segment pins connection.
• The result shows that the implementation of the function E is
needless.
• It is also obvious that the simplification step made us in rich of
designing and implementing a driver circuit for the 7- segment
display.
pins a b c d e f g
connection g g Vcc VccL Lg
Faculty Of Engineering Cairo University 2-Bit Comparator

12. Faculty Of Engineering Cairo University 2-Bit Comparator
• circuit simulation on proteus.DSN