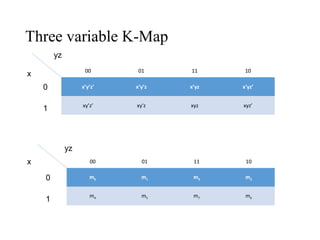
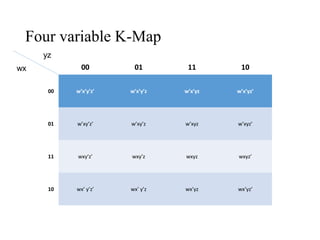
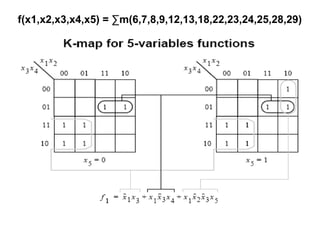
The document discusses the simplification of Boolean functions using Karnaugh maps and tabulation methods, detailing the challenges of algebraic minimization. It introduces Karnaugh maps as a graphical tool that organizes truth table data to simplify logic circuits through the identification of adjacent squares. The document also outlines principles for grouping these squares effectively for minimization.

1. Simplification of Boolean functions
by Karnaugh Map and Tabulation
Method
Presented By
C.Ramesh
Assistant Professor/ECE
KIT-kalaignarkarunanidhi Institute Of Technology,
Ciombatore.

2. Introduction
• Although the truth table representation of a function is unique,
when expressed algebraically, it can appear in many different form.
• Boolean functions may be simplified by algebraic means.
• How ever, this procedure of minimization is difficult because it
takes specific rules to predict each succeeding step in the
manipulative process.
• The map method provides a simple straight forward procedure for
minimizing Boolean functions.

3. Karnaugh Map (K-Map)
• A K-Map is a graphical representation of a truth table that can be
used to reduce a logic circuit to its simplest terms.
• The Karnaugh map uses a rectangle divided into rows and
columns.
• Any product term in the expression to be simplified can be
represented as the intersection of a row and a column.
• The rows and columns are labeled with each term in the expression
and its complement.
• The labels must be arranged so that each horizontal or vertical
move changes the state of one and only one variable.

4. Two variable K-Map
x’y’ x’y
xy’ xy
x
y
0
0
1
1
m0 m1
m2 m3
x
y
0
0
1
1

5. Three variable K-Map
x’y’z’ x’y’z x’yz x’yz’
xy’z’ xy'z xyz xyz’
m0 m1 m3 m2
m4 m5 m7 m6
x
x
yz
yz
0
1
0
1
00 01 11 10
00 01 11 10

6. Four variable K-Map
m0 m1 m3 m2
m4 m5 m7 m6
m12 m13 m15 m14
m8 m9 m11 m10
00 01 11 10
00
01
11
10
wx
yz

7. Four variable K-Map
w’x’y’z’ w’x’y’z w’x’yz w’x’yz’
w’xy’z’ w’xy’z w’xyz w’xyz’
wxy’z’ wxy’z wxyz wxyz’
wx’ y’z’ wx’ y’z wx’yz wx’yz’
00 01 11 10
00
01
11
10
wx
yz

8. Simplification Using the K-Map
• Look for adjacent squares.
• Adjacent squares are those squares where only one variable
changes as one moves from a square to another.
• Group adjacent squares in powers of two, i.e. pairs, quads,
groups of eight, groups of 16, etc.
• Principle 1. “The more, the merrier.” Hence, a quad is better
than a pair.
• Principle 2. Share group elements only when necessary to form
another or bigger group.

9. f(A,B) = ∑m(1,2,3)
f(A,B) = ∑m(0,1)

10. f(x1,x2,x3) = ∑m(0,1,2,3,6)
f(x1,x2,x3) = ∑m(2,3,4,6)

16. f(x1,x2,x3,x4,x5) = ∑m(6,7,8,9,12,13,18,22,23,24,25,28,29)

17. f(a,b,c,d,e) = ∑m(0,2,6,8,9,10,11,18,22,26,24,25,27,30)

21. POS Simplification
00 01 11 10
00 1 1 0 1
01 0 1 0 0
11 0 0 0 0
10 1 1 0 1
Simplify the function f(A,B,C,D)=Σ(0,1,2,5,8,9,10) in sum of
products and product of sums.
00 01 11 10
00 1 1 1
01 1
11
10 1 1 1

22. POS Simplification
00 01 11 10
00 0
01 0 0 0
11 0 0 0 0
10 0
f(A,B,C,D)=(A’+B’)(C’+D’)(B’+D)
f‘(A,B,C,D)=AB+CD+BD’

26. Minimize the following Boolean functions by K-Map

27. THANK YOU