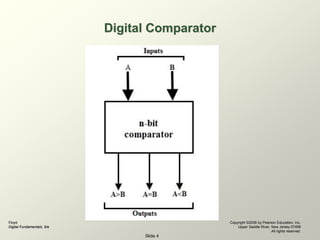
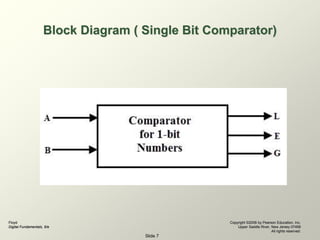
The document discusses comparators, which are combinational logic circuits that compare the magnitudes of two binary numbers and determine their relationship. It describes 1-bit, 2-bit, and 4-bit comparators and how they use logic gates like XOR gates to compare bits and output if the numbers are equal, if the first is greater than the second, or if the first is less than the second. Larger comparators can be built by cascading multiple comparator circuits to compare numbers with more bits.