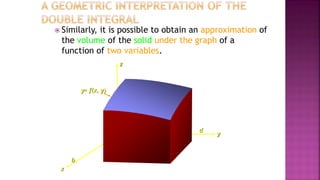
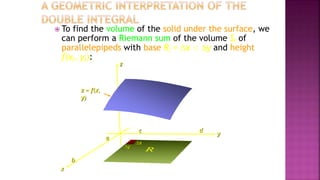
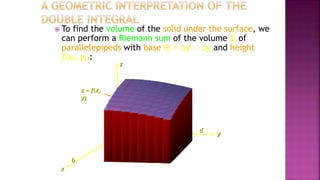
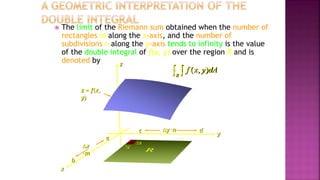
1. Double integrals allow us to calculate the volume of a solid bounded above by a surface z=f(x,y) and below by a plane region R. This is done by setting up a Riemann sum of the volumes of thin rectangular prisms. 2. The limit of the Riemann sum as the number of rectangles goes to infinity gives the double integral, written as ∫∫R f(x,y) dA. 3. Example problems demonstrate calculating the double integral to find the volume in different plane regions R, including those bounded by curves such as y=x2 and y=x.

1. Double Integrals
z
x
y
2
1
y x
 
2
1
y x
 
R
z = f(x, y) = y

2.  You may recall that we can do a Riemann sum to
approximate the area under the graph of a function
of one variable by adding the areas of the
rectangles that form below the graph resulting from
small increments of x (x) within a given interval
[a, b]:
x
y
y= f(x)
a b
x

3. z
 Similarly, it is possible to obtain an approximation of
the volume of the solid under the graph of a
function of two variables.
y
x
a
b
c d
R
y= f(x, y)

4. a. Suppose g1(x) and g2(x) are continuous functions on [a, b] and
the region R is defined by R = {(x, y)| g1(x)  y  g2(x); a  x  b}.
Then,
2
1
( )
( )
( , ) ( , )
b g x
R a g x
f x y dA f x y dy dx
 

 
 
   
x
y
a b
y = g1(x)
y = g2(x)
R

5.  Let R be a region in the xy-plane and let f
be continuous and nonnegative on R.
 Then, the volume of the solid under a
surface bounded above by z = f(x, y) and
below by R is given by
( , )
R
V f x y dA
  

6. z
 To find the volume of the solid under the surface, we
can perform a Riemann sum of the volume Si of
parallelepipeds with base Ri = x ☓ y and height
f(xi, yi):
y
x
a
b
c d
x
y
z = f(x,
y)
R

7. z
 To find the volume of the solid under the surface, we
can perform a Riemann sum of the volume Si of
parallelepipeds with base Ri = x ☓ y and height
f(xi, yi):
y
x
a
b
c d
x
y
Si
z = f(x,
y)
R

8. y
a
b
c d
z
x
 To find the volume of the solid under the surface, we
can perform a Riemann sum of the volume Si of
parallelepipeds with base Ri = x ☓ y and height
f(xi, yi):
z = f(x,
y)

9. z
 The limit of the Riemann sum obtained when the number of
rectangles m along the x-axis, and the number of
subdivisions n along the y-axis tends to infinity is the value
of the double integral of f(x, y) over the region R and is
denoted by
z = f(x,
y)
y
x
a
b
c d
x
y
R
( , )
R
f x y dA
 
y ·n
x
·m

10. b. Suppose h1(y) and h2(y) are continuous functions on [c, d]
and the region R is defined by R = {(x, y)| h1(y)  x 
h2(y); c  y  d}.
Then, 2
1
( )
( )
( , ) ( , )
d h y
R c h y
f x y dA f x y dx dy
 

 
 
   
x
y
c
d
x = h1(y) x = h2(y)
R

11. 4
3
2
1
1 2 3 4
 Evaluate ∫R∫f(x, y)dA given that f(x, y) = x2 + y2 and
R is the region bounded by the graphs of g1(x) = x
and g2(x) = 2x for 0  x  2.
Solution
 The region under consideration is:
x
g2(x) = 2x
R
y
g1(x) = x
Example 2, page 593

12.  Evaluate ∫R∫f(x, y)dA given that f(x, y) = x2 + y2 and
R is the region bounded by the graphs of g1(x) = x
and g2(x) = 2x for 0  x  2.
Solution
 Using Theorem 1, we find:
2 2
2 2
0
( , ) ( )
x
R x
f x y dA x y dy dx
 
 
 
 
   
2
2
2 3
0
1
3
x
x
x y y dx
 
 
 
 
 
 
 
 

2
3 3 3 3
0
8 1
2
3 3
x x x x dx
 
   
   
   
 
   
 

2
3
0
10
3
x dx
 
2
4
0
5
6
x
 1
3
13

Example 2, page 593

13. 1
1
 Evaluate ∫R∫f(x, y)dA, where f(x, y) = xey and R is the
plane region bounded by the graphs of y = x2 and y = x.
Solution
 The region under consideration is:
x
g1(x) = x2
R
y
g2(x) = x
 The points of intersection of
the two curves are found by
solving the equation x2 = x,
giving x = 0 and x = 1.
Example 3, page 593

14.  Evaluate ∫R∫f(x, y)dA, where f(x, y) = xey and R is
the plane region bounded by the graphs of y = x2
and y = x.
Solution
 Using Theorem 1, we find:
2
1
0
( , )
x
y
R x
f x y dA xe dy dx
 

 
 
      2
1
0
x
y
x
xe dx
 

 
 

2
1
0
( )
x x
xe xe dx
 

2
1 1
0 0
x x
xe dx xe dx
 
 
2
1
0
1
( 1)
2
x x
x e e
 
  
 
 
1 1 1
1 (3 )
2 2 2
e e
 
      
 
 
Integrating by parts on
the right-hand side
Example 3, page 593

15.  Find the volume of the solid bounded above by the
plane z = f(x, y) = y and below by the plane
region R defined by
Solution
 The graph of the region R is:
1
1
x
y
2
1
y x
 
R
 Observe that f(x, y) = y > 0 for (x, y) ∈ R.
2
1 (0 1)
y x x
   
Example 4, page 594

16.  Find the volume of the solid bounded above by the
plane z = f(x, y) = y and below by the plane
region R defined by
Solution
 Therefore, the required volume is given by
2
1 1
0 0
x
R
V ydA ydy dx

 
   
 
   
2
1
1
2
0
0
1
2
x
y dx

 
 

 
 

1
2
0
1
(1 )
2
x dx
 

1
3
0
1 1
2 3
x x
 
 
 
 
1
3

2
1 (0 1)
y x x
   
Example 4, page 594

17.  Find the volume of the solid bounded above by the
plane z = f(x, y) = y and below by the plane region
R defined by
Solution
2
1 (0 1)
y x x
   
z
x
y
 The graph of the solid
in question is:
2
1
y x
 
R
z = f(x, y) = y
Example 4, page 594