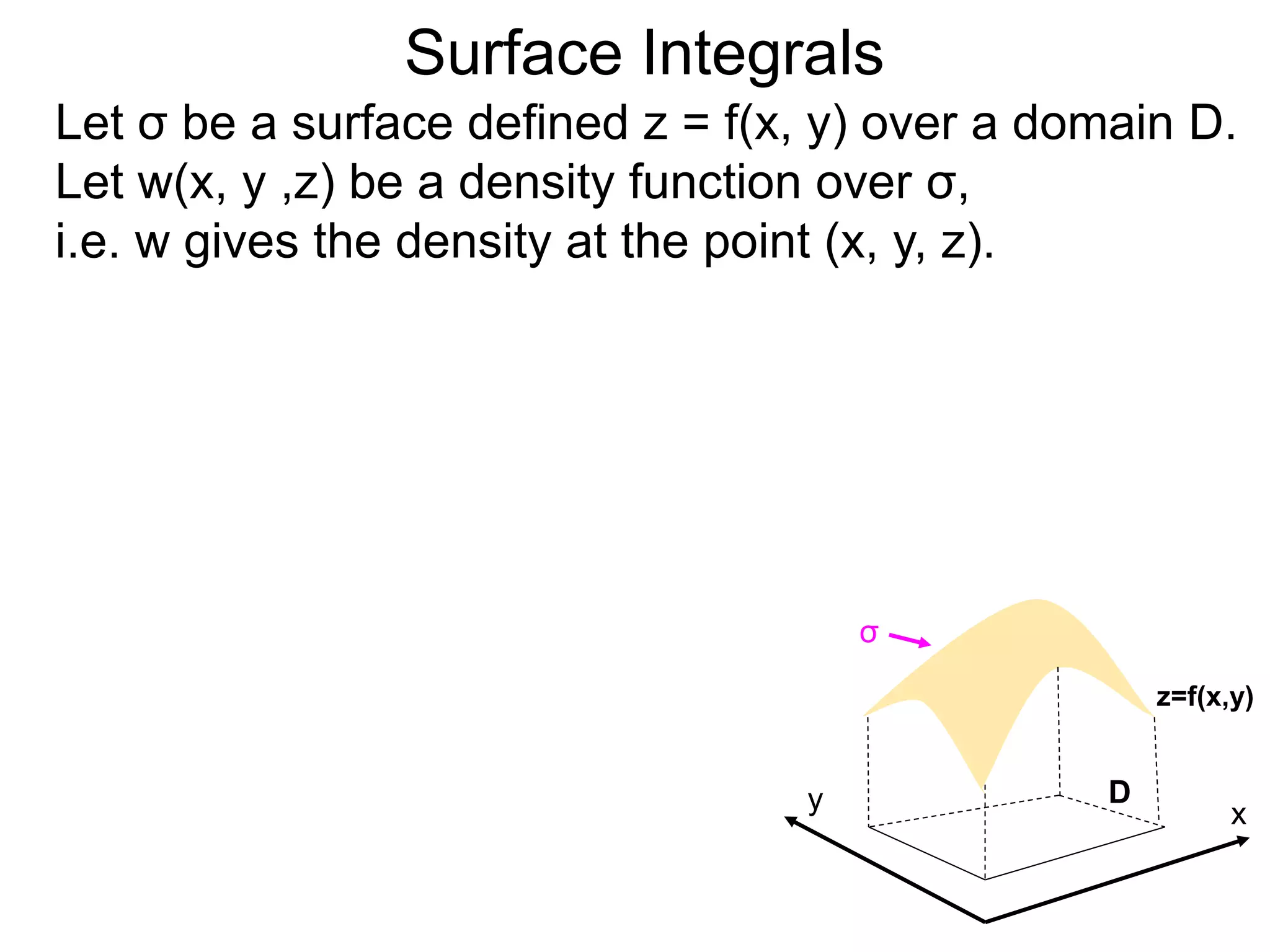
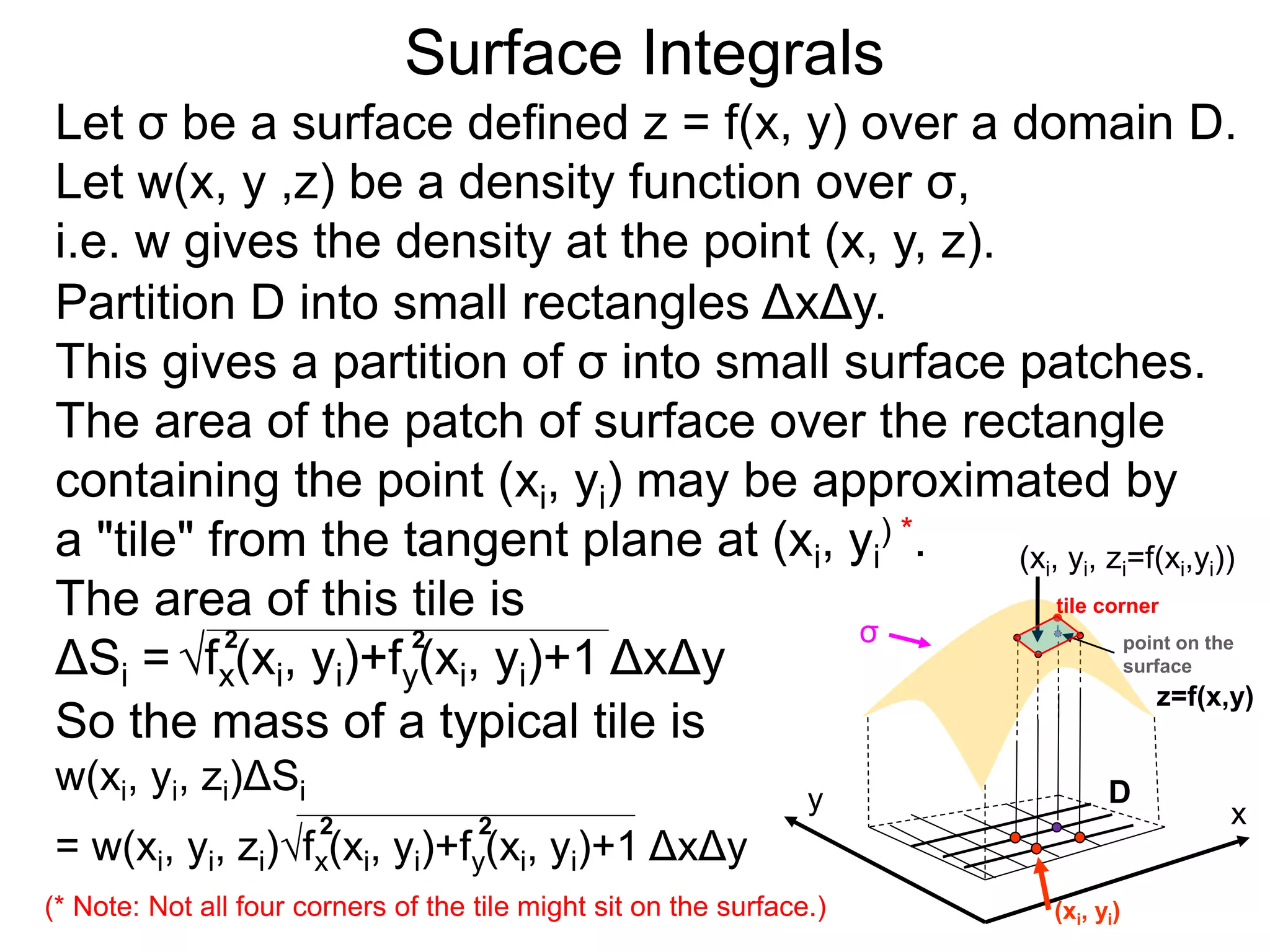
The document discusses surface integrals. It defines a surface σ as z=f(x,y) over a domain D. A density function w(x,y,z) gives the density at each point on σ. The surface is partitioned into small patches, and the area of each patch is approximated using the tangent plane at that point. The total mass of the surface is calculated as the integral of w over σ, with the surface differential dS representing the area of each small patch. An example calculates the mass of a surface in the first octant given a density function w(x,y,z)=xz.

1. Surface Integrals

2. Surface Integrals
Fact: Given a tilted
parallelogram in 3D over the
domain [0,1] x [0, 1].
x
y
z
1
1

3. Surface Integrals
Fact: Given a tilted
parallelogram in 3D over the
domain [0,1] x [0, 1].
Let M and L be the slopes
in the x–direction and in the
y–direction respectively,
x
y
z
1
1

4. Surface Integrals
Fact: Given a tilted
parallelogram in 3D over the
domain [0,1] x [0, 1].
Let M and L be the slopes
in the x–direction and in the
y–direction respectively,
x
y
z
M
1
1

5. Surface Integrals
Fact: Given a tilted
parallelogram in 3D over the
domain [0,1] x [0, 1].
Let M and L be the slopes
in the x–direction and in the
y–direction respectively,
1
1
x
y
z
M
L

6. Surface Integrals
Fact: Given a tilted
parallelogram in 3D over the
domain [0,1] x [0, 1].
Let M and L be the slopes
in the x–direction and in the
y–direction respectively,
1
1
x
y
z
M
L
L

7. Surface Integrals
Fact: Given a tilted
parallelogram in 3D over the
domain [0,1] x [0, 1].
Let M and L be the slopes
in the x–direction and in the
y–direction respectively,
by cross product, the area of
the parallelogram is M2 + L2 + 1.
1
1
x
y
z
M
L
L

8. Surface Integrals
1
1
x
y
z
M
L
L
In general, if the domain is
[0,Δx] x [0, Δy] instead,
then its area is
M2 + L2 + 1 ΔxΔy
Δx
Δy
x
y
z
MΔx
LΔy
LΔy
MΔx
Fact: Given a tilted
parallelogram in 3D over the
domain [0,1] x [0, 1].
Let M and L be the slopes
in the x–direction and in the
y–direction respectively,
by cross product, the area of
the parallelogram is M2 + L2 + 1.

9. Surface Integrals
Let σ be a surface defined z = f(x, y) over a domain D.
x
y D
z=f(x,y)
σ

10. Surface Integrals
Let σ be a surface defined z = f(x, y) over a domain D.
Let w(x, y ,z) be a density function over σ,
i.e. w gives the density at the point (x, y, z).
x
y D
z=f(x,y)
σ

11. Surface Integrals
Let σ be a surface defined z = f(x, y) over a domain D.
Let w(x, y ,z) be a density function over σ,
i.e. w gives the density at the point (x, y, z).
Partition D into small rectangles ΔxΔy.
This gives a partition of σ into small surface patches.
x
y D
z=f(x,y)
σ

12. Surface Integrals
Let σ be a surface defined z = f(x, y) over a domain D.
Let w(x, y ,z) be a density function over σ,
i.e. w gives the density at the point (x, y, z).
Partition D into small rectangles ΔxΔy.
This gives a partition of σ into small surface patches.
The area of the patch of surface over the rectangle
containing the point (xi, yi) may be approximated by
a "tile" from the tangent plane at (xi, yi
) *.
x
y D
z=f(x,y)
σ

13. Surface Integrals
Let σ be a surface defined z = f(x, y) over a domain D.
Let w(x, y ,z) be a density function over σ,
i.e. w gives the density at the point (x, y, z).
Partition D into small rectangles ΔxΔy.
This gives a partition of σ into small surface patches.
The area of the patch of surface over the rectangle
containing the point (xi, yi) may be approximated by
a "tile" from the tangent plane at (xi, yi
) *.
x
y
(xi, yi, zi=f(xi,yi))
D
(xi, yi)
σ
z=f(x,y)

14. Surface Integrals
Let σ be a surface defined z = f(x, y) over a domain D.
Let w(x, y ,z) be a density function over σ,
i.e. w gives the density at the point (x, y, z).
Partition D into small rectangles ΔxΔy.
This gives a partition of σ into small surface patches.
The area of the patch of surface over the rectangle
containing the point (xi, yi) may be approximated by
a "tile" from the tangent plane at (xi, yi
) *.
x
y
(xi, yi, zi=f(xi,yi))
D
(xi, yi)
σ
z=f(x,y)
(* Note: Not all four corners of the tile might sit on the surface.)

15. Surface Integrals
Let σ be a surface defined z = f(x, y) over a domain D.
Let w(x, y ,z) be a density function over σ,
i.e. w gives the density at the point (x, y, z).
Partition D into small rectangles ΔxΔy.
This gives a partition of σ into small surface patches.
The area of the patch of surface over the rectangle
containing the point (xi, yi) may be approximated by
a "tile" from the tangent plane at (xi, yi
) *.
x
y
(xi, yi, zi=f(xi,yi))
D
(xi, yi)
σ
z=f(x,y)
(* Note: Not all four corners of the tile might sit on the surface.)
tile corner
point on the
surface

16. Surface Integrals
Let σ be a surface defined z = f(x, y) over a domain D.
Let w(x, y ,z) be a density function over σ,
i.e. w gives the density at the point (x, y, z).
Partition D into small rectangles ΔxΔy.
This gives a partition of σ into small surface patches.
The area of the patch of surface over the rectangle
containing the point (xi, yi) may be approximated by
a "tile" from the tangent plane at (xi, yi
) *.
The area of this tile is
ΔSi =
x
y
(xi, yi, zi=f(xi,yi))
D
(xi, yi)
fx(xi, yi)+fy(xi, yi)+1 ΔxΔy
2 2 σ
z=f(x,y)
(* Note: Not all four corners of the tile might sit on the surface.)
tile corner
point on the
surface

17. Surface Integrals
Let σ be a surface defined z = f(x, y) over a domain D.
Let w(x, y ,z) be a density function over σ,
i.e. w gives the density at the point (x, y, z).
So the mass of a typical tile is
w(xi, yi, zi)ΔSi
= w(xi, yi, zi)fx(xi, yi)+fy(xi, yi)+1 ΔxΔy
2 2
Partition D into small rectangles ΔxΔy.
This gives a partition of σ into small surface patches.
The area of the patch of surface over the rectangle
containing the point (xi, yi) may be approximated by
a "tile" from the tangent plane at (xi, yi
) *.
The area of this tile is
ΔSi =fx(xi, yi)+fy(xi, yi)+1 ΔxΔy
2 2
(* Note: Not all four corners of the tile might sit on the surface.)
x
y
(xi, yi, zi=f(xi,yi))
D
(xi, yi)
σ
z=f(x,y)
tile corner
point on the
surface

18. Surface Integrals
Hence the total mass of the surface σ over D is
M = Σ w(xi, yi, zi)fx(xi, yi)+fy(xi, yi)+1 ΔxΔy
2 2
lim Δx0
lim Δy0

19. Surface Integrals
Hence the total mass of the surface σ over D is
M = Σ w(xi, yi, zi)fx(xi, yi)+fy(xi, yi)+1 ΔxΔy
2 2
lim Δx0
lim Δy0
= ∫D
∫ w(x, y , z)fx(x, y)+fy(x, y)+1 dxdy or dydx
2 2
to be replaced by f(x,y)

20. Surface Integrals
Hence the total mass of the surface σ over D is
M = Σ w(xi, yi, zi)fx(xi, yi)+fy(xi, yi)+1 ΔxΔy
2 2
lim Δx0
lim Δy0
= ∫D
∫ w(x, y , z)fx(x, y)+fy(x, y)+1 dxdy or dydx
2 2
to be replaced by f(x,y)
Let the σ be the surface, we write this integral as
∫σ
∫ w(x, y, z) dS with z = f(x, y)

21. Surface Integrals
Hence the total mass of the surface σ over D is
M = Σ w(xi, yi, zi)fx(xi, yi)+fy(xi, yi)+1 ΔxΔy
2 2
lim Δx0
lim Δy0
= ∫D
∫ w(x, y , z)fx(x, y)+fy(x, y)+1 dxdy or dydx
2 2
to be replaced by f(x,y)
Let the σ be the surface, we write this integral as
∫σ
∫ w(x, y, z) dS
with dS =fx(x, y)+fy(x, y)+1 dA, i.e. dxdy or dydx.
2 2
with z = f(x, y)

22. Surface Integrals
Hence the total mass of the surface σ over D is
M = Σ w(xi, yi, zi)fx(xi, yi)+fy(xi, yi)+1 ΔxΔy
2 2
lim Δx0
lim Δy0
= ∫D
∫ w(x, y , z)fx(x, y)+fy(x, y)+1 dxdy or dydx
2 2
to be replaced by f(x,y)
Let the σ be the surface, we write this integral as
∫σ
∫ w(x, y, z) dS
with dS =fx(x, y)+fy(x, y)+1 dA, i.e. dxdy or dydx.
dS is called the surface differential. Often it’s easier
to visualized a surface integral problem as the sum
over dS–the areas of the small surface patches on σ,
2 2
with z = f(x, y)

23. Surface Integrals
Hence the total mass of the surface σ over D is
M = Σ w(xi, yi, zi)fx(xi, yi)+fy(xi, yi)+1 ΔxΔy
2 2
lim Δx0
lim Δy0
= ∫D
∫ w(x, y , z)fx(x, y)+fy(x, y)+1 dxdy or dydx
2 2
to be replaced by f(x,y)
Let the σ be the surface, we write this integral as
∫σ
∫ w(x, y, z) dS
with dS =fx(x, y)+fy(x, y)+1 dA, i.e. dxdy or dydx.
dS is called the surface differential. Often it’s easier
to visualized a surface integral problem as the sum
over dS–the areas of the small surface patches on σ,
but for the actual calculation, we need convert
dS to the dA–integral over the flat domain D.
2 2
with z = f(x, y)

24. Surface Integrals
Example A. Given w(x, y, z) = xz be the density
function over the surface x + y + z = 1 in the first
octant, find its mass.

25. Surface Integrals
Example A. Given w(x, y, z) = xz be the density
function over the surface x + y + z = 1 in the first
octant, find its mass.
x
y
1
1
D
σ
1

26. Surface Integrals
Example A. Given w(x, y, z) = xz be the density
function over the surface x + y + z = 1 in the first
octant, find its mass.
z = 1 – x – y on the surface σ.
x
y
1
1
D
σ
1

27. Surface Integrals
Example A. Given w(x, y, z) = xz be the density
function over the surface x + y + z = 1 in the first
octant, find its mass.
z = 1 – x – y on the surface σ.
Therefore
w(x, y, z) = xz = x(1 – x – y).
x
y
1
1
D
σ
1

28. Surface Integrals
Example A. Given w(x, y, z) = xz be the density
function over the surface x + y + z = 1 in the first
octant, find its mass.
z = 1 – x – y on the surface σ.
Therefore
w(x, y, z) = xz = x(1 – x – y).
zx = –1, zy = –1,
x
y
1
1
D
σ
1

29. Surface Integrals
Example A. Given w(x, y, z) = xz be the density
function over the surface x + y + z = 1 in the first
octant, find its mass.
z = 1 – x – y on the surface σ.
Therefore
w(x, y, z) = xz = x(1 – x – y).
zx = –1, zy = –1, so
dS = 12 + 12 + 1 dA
x
y
1
1
D
σ
1

30. Surface Integrals
Example A. Given w(x, y, z) = xz be the density
function over the surface x + y + z = 1 in the first
octant, find its mass.
z = 1 – x – y on the surface σ.
Therefore
w(x, y, z) = xz = x(1 – x – y).
zx = –1, zy = –1, so
dS = 12 + 12 + 1 dA = 3 dA
x
y
1
1
D
σ
1

31. Surface Integrals
Example A. Given w(x, y, z) = xz be the density
function over the surface x + y + z = 1 in the first
octant, find its mass.
So the mass = ∫σ
∫w(x, y , z) dS =
z = 1 – x – y on the surface σ.
Therefore
w(x, y, z) = xz = x(1 – x – y).
zx = –1, zy = –1, so
dS = 12 + 12 + 1 dA = 3 dA
x
y
1
1
D
σ
1

32. Surface Integrals
Example A. Given w(x, y, z) = xz be the density
function over the surface x + y + z = 1 in the first
octant, find its mass.
So the mass = ∫σ
∫w(x, y , z) dS =
z = 1 – x – y on the surface σ.
Therefore
w(x, y, z) = xz = x(1 – x – y).
zx = –1, zy = –1, so
dS = 12 + 12 + 1 dA = 3 dA
∫
D
∫x(1 – x – y)3 dA
x
y
1
1
D
σ
1

33. Surface Integrals
Example A. Given w(x, y, z) = xz be the density
function over the surface x + y + z = 1 in the first
octant, find its mass.
So the mass = ∫σ
∫w(x, y , z) dS =
z = 1 – x – y on the surface σ.
Therefore
w(x, y, z) = xz = x(1 – x – y).
zx = –1, zy = –1, so
dS = 12 + 12 + 1 dA = 3 dA
∫
D
∫x(1 – x – y)3 dA
=∫
x=0
∫x(1 – x – y)3 dydx =
1
y=0
1–x
x
y
1
1
D
σ
1

34. Surface Integrals
Example A. Given w(x, y, z) = xz be the density
function over the surface x + y + z = 1 in the first
octant, find its mass.
So the mass = ∫σ
∫w(x, y , z) dS =
z = 1 – x – y on the surface σ.
Therefore
w(x, y, z) = xz = x(1 – x – y).
zx = –1, zy = –1, so
dS = 12 + 12 + 1 dA = 3 dA
∫
D
∫x(1 – x – y)3 dA
=∫
x=0
∫x(1 – x – y)3 dydx =
1
y=0
1–x
3/24
x
y
1
1
D
σ
1

35. Surface Integrals
Example B. Find the surface integral
∫ ∫(x2 + y2)z dS
σ
x2 + y2 + z2 = 4 above the plane z = 1
where σ is the portion of the sphere

36. Surface Integrals
Example B. Find the surface integral
∫ ∫(x2 + y2)z dS
σ
x2 + y2 + z2 = 4 above the plane z = 1
where σ is the portion of the sphere
σ
D

37. Surface Integrals
Example B. Find the surface integral
z = 4 – x2 – y2
∫ ∫(x2 + y2)z dS
σ
x2 + y2 + z2 = 4 above the plane z = 1
where σ is the portion of the sphere
σ
D

38. Surface Integrals
Example B. Find the surface integral
z = 4 – x2 – y2 so (x2 + y2)z = (x2 + y2)4 – x2 – y2.
∫ ∫(x2 + y2)z dS
σ
x2 + y2 + z2 = 4 above the plane z = 1
where σ is the portion of the sphere
σ
D

39. Surface Integrals
Example B. Find the surface integral
z = 4 – x2 – y2 so (x2 + y2)z = (x2 + y2)4 – x2 – y2.
∫ ∫(x2 + y2)z dS
σ
x2 + y2 + z2 = 4 above the plane z = 1
where σ is the portion of the sphere
zx =
4 – x2 – y2
zx = –x
4 – x2 – y2
zy = –y
σ
D

40. Surface Integrals
Example B. Find the surface integral
z = 4 – x2 – y2 so (x2 + y2)z = (x2 + y2)4 – x2 – y2.
∫ ∫(x2 + y2)z dS
σ
x2 + y2 + z2 = 4 above the plane z = 1
where σ is the portion of the sphere
zx =
4 – x2 – y2
zx = –x
4 – x2 – y2
zy = –y
zx + zy + 1 =
2 2
4 – x2 – y2
4
σ
D

41. Surface Integrals
Example B. Find the surface integral
z = 4 – x2 – y2 so (x2 + y2)z = (x2 + y2)4 – x2 – y2.
∫ ∫(x2 + y2)z dS
σ
x2 + y2 + z2 = 4 above the plane z = 1
where σ is the portion of the sphere
zx =
So dS = 
4 – x2 – y2
zx = –x
4 – x2 – y2
zy = –y
zx + zy + 1 =
2 2
4 – x2 – y2
4
zx + zy + 1
2 2
σ
D
dA

42. Surface Integrals
Example B. Find the surface integral
z = 4 – x2 – y2 so (x2 + y2)z = (x2 + y2)4 – x2 – y2.
∫ ∫(x2 + y2)z dS
σ
x2 + y2 + z2 = 4 above the plane z = 1
where σ is the portion of the sphere
zx =
So dS = 
4 – x2 – y2
zx = –x
4 – x2 – y2
zy = –y
zx + zy + 1 =
2 2
4 – x2 – y2
4
 4 – x2 – y2
2
zx + zy + 1
2 2
= dA
σ
D
dA

43. Surface Integrals
The integrand
= (x2 + y2)4 – x2 – y2 *
 4 – x2 – y2
2
(x2 + y2)z dS is
dA

44. Surface Integrals
The integrand
= (x2 + y2)4 – x2 – y2 *
 4 – x2 – y2
2
(x2 + y2)z dS is
dA
= 2(x2 + y2)dA,

45. Surface Integrals
The integrand
= (x2 + y2)4 – x2 – y2 *
 4 – x2 – y2
2
(x2 + y2)z dS is
dA
= 2(x2 + y2)dA, integrated over the domain D of σ.

46. Surface Integrals
The integrand
= (x2 + y2)4 – x2 – y2 *
 4 – x2 – y2
2
(x2 + y2)z dS is
dA
= 2(x2 + y2)dA, integrated over the domain D of σ.
D is the circle x2 + y2 ≤ 3.
Using the polar form, we get:

47. Surface Integrals
The integrand
= (x2 + y2)4 – x2 – y2 *
 4 – x2 – y2
2
(x2 + y2)z dS is
dA
= 2(x2 + y2)dA, integrated over the domain D of σ.
∫σ
∫w(x, y , z) dS = ∫ ∫2(x2 + y2) dA =
D
D is the circle x2 + y2 ≤ 3.
Using the polar form, we get:

48. Surface Integrals
The integrand
= (x2 + y2)4 – x2 – y2 *
 4 – x2 – y2
2
(x2 + y2)z dS is
dA
= 2(x2 + y2)dA, integrated over the domain D of σ.
∫σ
∫w(x, y , z) dS = ∫ ∫ 2r2 * rdrd
r=0
3
=0
2π
∫ ∫2(x2 + y2) dA =
D
D is the circle x2 + y2 ≤ 3.
Using the polar form, we get:

49. Surface Integrals
The integrand
= (x2 + y2)4 – x2 – y2 *
 4 – x2 – y2
2
(x2 + y2)z dS is
dA
= 2(x2 + y2)dA, integrated over the domain D of σ.
∫σ
∫w(x, y , z) dS = ∫ ∫ 2r2 * rdrd
r=0
=0
2π
∫ ∫ 2r3 dr
r=0
=0
2π
= d *
∫ ∫2(x2 + y2) dA =
D
D is the circle x2 + y2 ≤ 3.
Using the polar form, we get:
3
3

50. Surface Integrals
The integrand
= (x2 + y2)4 – x2 – y2 *
 4 – x2 – y2
2
(x2 + y2)z dS is
dA
= 2(x2 + y2)dA, integrated over the domain D of σ.
∫σ
∫w(x, y , z) dS = ∫ ∫ 2r2 * rdrd
r=0
=0
2π
∫ ∫ 2r3 dr
r=0
=0
2π
= d *
= 2π* 9/2 = 9π
∫ ∫2(x2 + y2) dA =
D
D is the circle x2 + y2 ≤ 3.
Using the polar form, we get:
3
3