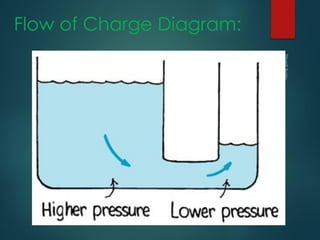
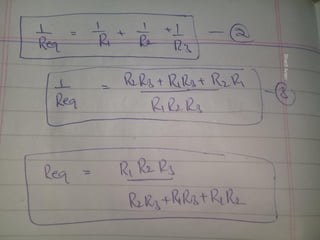
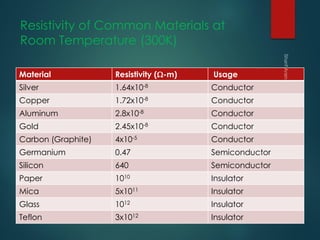
1. The document covers basic electrical concepts including circuits, charge, voltage, current, resistance, Ohm's law, conductors, insulators, semiconductors, and measurement devices. 2. Key concepts discussed include Kirchhoff's current and voltage laws, factors that influence resistance, and applications of electrical concepts like batteries and power supplies. 3. Engineering concepts such as resistivity of materials and its relationship to resistance through geometry are examined alongside historical scientists like Ohm, Ampere, and Volta who contributed to the field.

1. 1. Circuit (1)
2. Charge (3-5)
3. Voltage (6-15)
4. Current (16-22)
5. Resistance (23-29)
6. Current and voltage (30-31)
7. Resistance and current (32)
8. Ohm’s Law (33-38)
9. Electrical machine (39-40)
10. Conductor and Insulator (42-44)
11. Semiconductor (45)
12. Ammeter and voltmeter (46-50)
13. Single phase and Triple phase
(51-55)
14. KVL and KCL (56- 62)
15. Resistance in series and parallel
(63-65)
Basic Electrical Engineering (MID COURSE)
By Engr Sharif Ur Rahman
Sharif Arain

2. Circuits
 Closed Circuit
 Allows a complete path for electrons to travel
 Open Circuit
 Does not allow a complete path for the electrons to
travel

3. Flow of Charge
 When the ends of an
electric conductor are at
different electric potentials
(voltages)
Charge continues to flow
until the ends of the
conductor has the same
voltage

4. Charge
 Electrical property of atomic particles
 Electrons are negatively charged
 Protons are positivity charged
 The absolute value of the charge on an electron is 1.6x10-
19 C
 The symbol used is Q or q

5. Flow of Charge Diagram:

7. Alessandro Volta (1745 – 1827)
 Italian physicist
 known especially for
the invention of the
electrochemical cell,
aka the battery in
1800.

8. Voltage
 The flow of charge is established by an external “pressure”
derived from the energy that a mass has by virtue of its position:
Potential energy
 Energy: the capacity/ability of to do work
1. Kinetic energy: Energy an object has due to its motion
2. Potential energy
 If a mass (m) is raised to some height (h) above a reference plane,
it has a measure of potential energy expressed in joules (J) that is
determined by
 W (potential energy) = mgh
where g is the gravitational acceleration (9.8 m/s2)
o Energy that is stored
o Potential energy due to an object’s position

9. Explanation:
 Potential difference between two points
 Either side of a voltage source is not an eqipotential
surface
 A wire is an equipotential surface
 It has the same potential
 If the wire is attached to a voltage source it is still an
equipotential surface

10. Equation:
 The electromotive force (emf) that causes charge
to move.
 1 Volt = 1 Joule/1 Coulomb
Q
W
V
dq
dw


 ;v

11.  Note:
 A potential difference or voltage is always
measured between two points in the system.
 Changing either point may change the potential
difference between the two points under
investigation.
 Potential difference between two points is
determined by: V = W/Q (volts)

12. Voltage unit define:
 A potential difference of 1 volt (V) exists between
two points if 1 joule (J) of energy is exchanged in
moving 1 coulomb (C) of charge between the
two points
 The unit of measurement volt was chosen to
honor Alessandro Volta

13. Summary
 The applied potential difference (in volts) of a
voltage source in an electric circuit is the
“pressure” to set the system in motion and
“cause” the flow of charge or current through the
electrical system.

14. Ideal Voltage Sources
 Independent voltage source outputs a voltage, either
dc or time varying, to the circuit no matter how much
current is required.

15. Note:
 Potential difference: The algebraic difference in
potential (or voltage) between two points of a network.
 Voltage: When isolated, like potential, the voltage at a
point with respect to some reference such as ground.
 Voltage difference: The algebraic difference in voltage
(or potential) between two points of a system. A
voltage drop or rise is as the terminology would
suggest.
 Electromotive force (emf): The force that establishes
the flow of charge (or current) in a system due to the
application of a difference in potential.

16. Current
 “The flow of free electron in a copper wire or any other solid
conductor of electricity”
 With no external forces applied, the net flow of charge in a
conductor in any one direction is zero
 Basic electric circuit
 Charge will only flow if there is a voltage source (potential
difference).
 The flow of electric charge
 The loosely bound outer electrons of conductors
carry the charge through circuits
 Protons tightly bound to the nuclei of atoms

17. André Ampère (1775 – 1836)
 French physicist and
mathematician.
 One of the main
discoverers of
electromagnetism.
 SI unit of measurement of
electric current, the
ampere, is named after
him.

18. Equation/formula:
 The flow of charge through a cross-sectional area as a
function of time or the time rate of change of charge
 Symbol used is I or i
)(;
;
12
2
1
ttIQdtiQ
t
Q
I
dt
dq
i
t
t






19. current = charge / time
or
I = q/t
Units: Amps (A)
An amp is the flow of 1 C of charge
per second
NOTE: 1 C = the charge of
6,240,000,000,000,000,000 electrons

20. Current’s Direction
 Electrons Travel from – to +
 Current is actually the opposite direction of the
flow of electrons

21. Current Sources
 An ideal current source outputs a dc or ac current to
the circuit no matter how much voltage is required.
 There are no ideal current sources as all known
current sources are unable to generate an unlimited
force (voltage) that is needed to deliver a constant
current to a circuit.

22. Summary
 Safety considerations
 Even small levels of current through the human
body can cause serious, dangerous side effects
 Any current over 10 mA is considered dangerous
 currents of 50 mA can cause severe shock
 currents over 100 mA can be fatal
 Treat electricity with respect – not fear

23. Electric Resistance
 “The ability of a material to resist the flow of charge”
 Units: Ohms (W)
 The amount of charge that flows through a circuit
depends on two things:
1. Voltage provided by source
2. Electric resistance of the conductor
 opposes the push from the voltage source.
 Resistance affects the speed of the current.

24. Georg Ohm (1789 – 1854)
 German physicist
 Ohm determined that
there is a direct
proportionality between
the voltage applied
across a conductor and
the electric current.
 This relationship is known
as Ohm's law.

25. Equation:
 Resistance takes into account the
physical dimensions of the material
where:
 L is the length of
conductor along which
the carriers are moving
 A is the cross sectional
area of the conductor
that the free electron
move through.
 ρ is the specific resistivity
of a material
A
L
R 

27. Resistivity, 
 Resistivity is a material property
 Dependent on the number of free electron or
mobile charges (usually electrons) in the material.
 In a metal, this is the number of electrons from the
outer shell that are ionized and become part of the
‘sea of electrons’
 Dependent on the mobility of the charges
 Mobility is related to the velocity of the charges.
 It is a function of the material, the frequency and
magnitude of the voltage applied to make the
charges move, and temperature.

28. Resistivity of Common Materials at
Room Temperature (300K)
Material Resistivity (W-m) Usage
Silver 1.64x10-8 Conductor
Copper 1.72x10-8 Conductor
Aluminum 2.8x10-8 Conductor
Gold 2.45x10-8 Conductor
Carbon (Graphite) 4x10-5 Conductor
Germanium 0.47 Semiconductor
Silicon 640 Semiconductor
Paper 1010 Insulator
Mica 5x1011 Insulator
Glass 1012 Insulator
Teflon 3x1012 Insulator

29. Electric Resistance Factors
Thick wires have less resistance than
thin wires
Short wires have less resistance than
long wires
Higher temperatures usually cause
more resistance
The resistance in some materials
becomes almost zero at very low
temperatures

30. Current vs. Voltage
Current – Flow rate
Measured in Amperes
Amount of flowing water
Voltage – Potential
Measured in Volts
Water Pressure

31.  If the voltage in a circuit increases,
the current will increase.
 If the voltage in a circuit decreases,
the current will decrease.
 This is a direct proportional
relationship.

32. Resistance and Current
 If the resistance in a circuit
increases, the current will
decrease.
 If the resistance in a circuit
decreases, the current will
increase.
 This is an inversely proportional
relationship.

33. OHM’S Law:
 State the relationship between
current, voltage, and resistance.
 German physicist George Ohm had
the law named after him, because of
his extensive research.

36. V=IR
Ohm’s Law
Voltage is equal to the current multiplied by
the resistance.
Voltage,
measured in
Volts, V
Current, measured
in Amps, A
Resistance,
measured in
Ohms, Ω

37. Ohm’s Law Examples…
If you want to find
Voltage in Volts:
V = IR
If I= 2 A and R = 5 Ohms
Then, V= (2A)(5Ω) = 10 V

38. Examples…
If you want to find Resistance in
Ohm’s:
R = V / I
If V = 9 Volts and I = 4 A
Then R = 9 V/ 4A = 2.25 Ω

39. Electrical Machine:

42. Conductance, G
 Conductance is the reciprocal of resistance
G = R-1 = i/v
Unit for conductance is S (siemens) or (mhos)
G = As/L
where s is conductivity,
which is the inverse of resistivity, 

43. Conductors and Insulators
 Conductors are those materials that permit a generous flow of
electrons with very little external force (voltage) applied
In addition,
 Good conductors typically have only one electron in the valance
(most distant from the nucleus) ring.

44.  Insulators are those materials that have very few
free electrons and require a large applied
potential (voltage) to establish a measurable
current level
 Insulators are commonly used as covering for
current-carrying wire, which, if uninsulated, could
cause dangerous side effects
 Rubber gloves and rubber mats are used to help
insulated workers when working on power lines
 Even the best insulator will break down if a
sufficiently large potential is applied across it

45. Semiconductors
 Semiconductors are a specific group of elements that
exhibit characteristics between those of insulators and
conductors
 Semiconductor materials typically have four electrons
in the outermost valence ring
 Semiconductors are further characterized as being
photoconductive and having a negative temperature
coefficient
 Photoconductivity: Photons from incident light can increase
the carrier density in the material and thereby the charge flow
level
 Negative temperature coefficient: Resistance will decrease
with an increase in temperature (opposite to that of most
conductors)

46. Ammeters and Voltmeters
 Ammeter (Millimeters or Micro ammeter)
 Used to measure current levels
 Must be placed in the network such that the
charge will flow through the meter
 Voltmeter
 Used to measure the potential difference between
two points

47.  Volt-ohm-milliammeter (VOM) and digital
multimeter (DMM)
 Both instruments will measure voltage and current and a third
quantity, resistance
 The VOM uses an analog scale, which requires interpreting the
position of the pointer on a continuous scale
 The DMM provides a display of numbers with decimal point accuracy
determined by the chosen scale.

48. Applications
 Flashlight
 Simplest of electrical circuits
 Batteries are connected in series to provide a
higher voltage (sum of the battery voltages)

49. Applications
 12-V Car battery charger
 Used to convert 120-V ac outlet power to dc charging power for
a 12-V automotive battery, using a transformer to step down the
voltage, diodes to rectify the ac (convert it to dc), and in some
cases a regulator to provide a dc voltage that varies with level of
charge.

50. Applications
 Answering machines/Phones dc supply
 A wide variety of devices receive their dc
operating voltage from an ac/dc conversion
system
 The conversion system uses a transformer to step
the voltage down to the appropriate level, then
diodes “rectify” the ac to dc, and capacitors
provide filtering to smooth out the dc.

58. Kirchhoff’s Current Law (KCL)
 The sum of currents entering any point in a circuit is equal to the sum of currents leaving
that point.
 Otherwise, charge would accumulate at the point, reducing or obstructing the
conducting path.
 The algebraic sum of currents entering a node is zero
 Add each branch current entering the node and subtract each branch current leaving
the node
 Σ currents in - Σ currents out = 0
 Or Σ currents in = Σ currents out
 Kirchhoff’s Current Law may also be stated as
IIN = IOUT
AND





nodenode
1
0
leaveenter
N
n
n
ii
i Where N is the total number of
branches connected to a node.

59. Kirchhoff's Voltage Law
(KVL)
 The algebraic sum of voltages around each loop
is zero
 Beginning with one node, add voltages across
each branch in the loop (if you encounter a + sign
first) and subtract voltages (if you encounter a –
sign first)
 Σ voltage drops - Σ voltage rises = 0
 Or Σ voltage drops = Σ voltage rises

60. Kirchhoff’s Voltage Law
 Or KVL for short
 Based upon conservation of energy – the algebraic
sum of voltages dropped across components
around a loop is zero.
 




risesdrops
M
1m
vv
0v Where M is the total number of
branches in the loop.