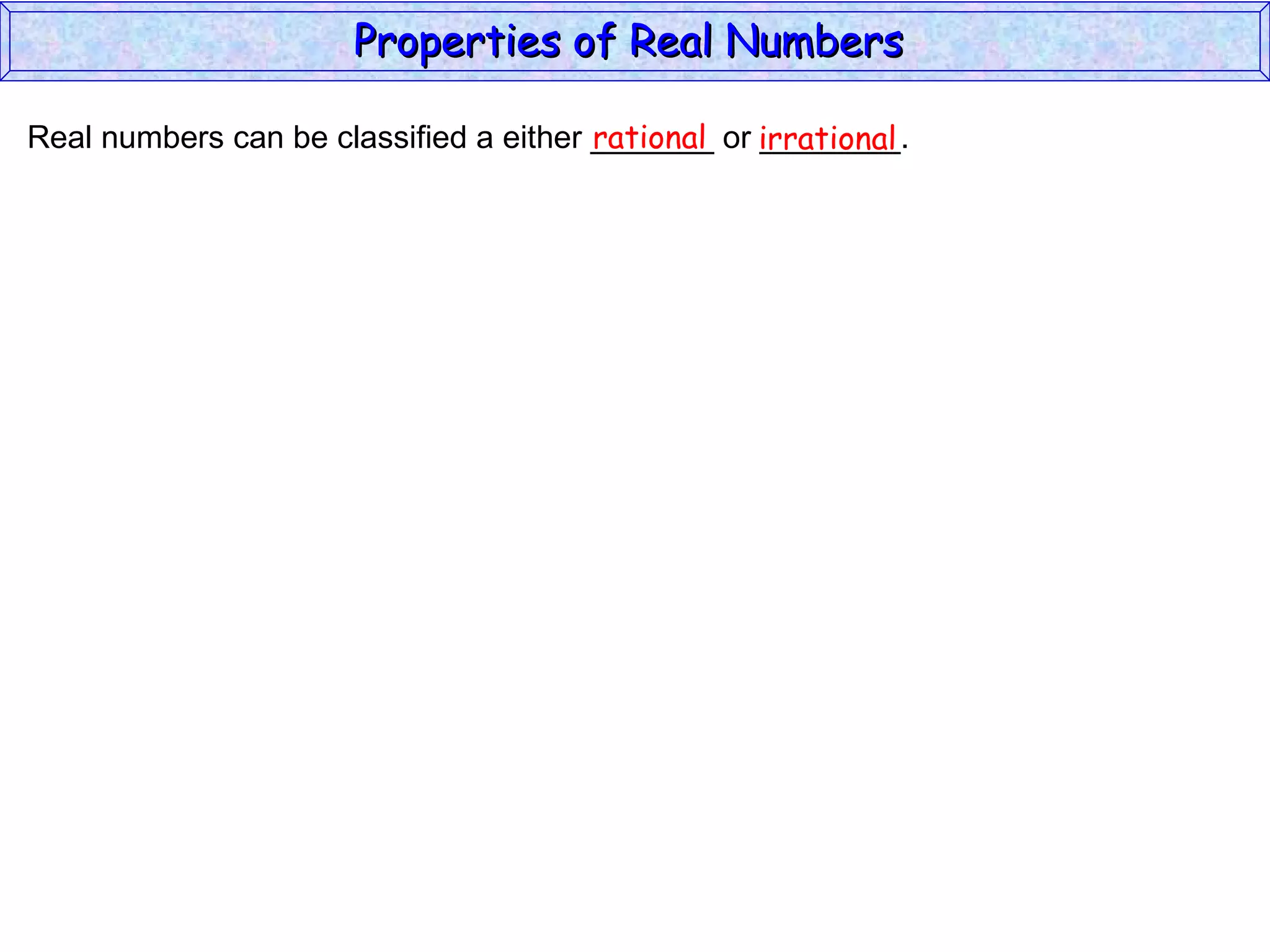
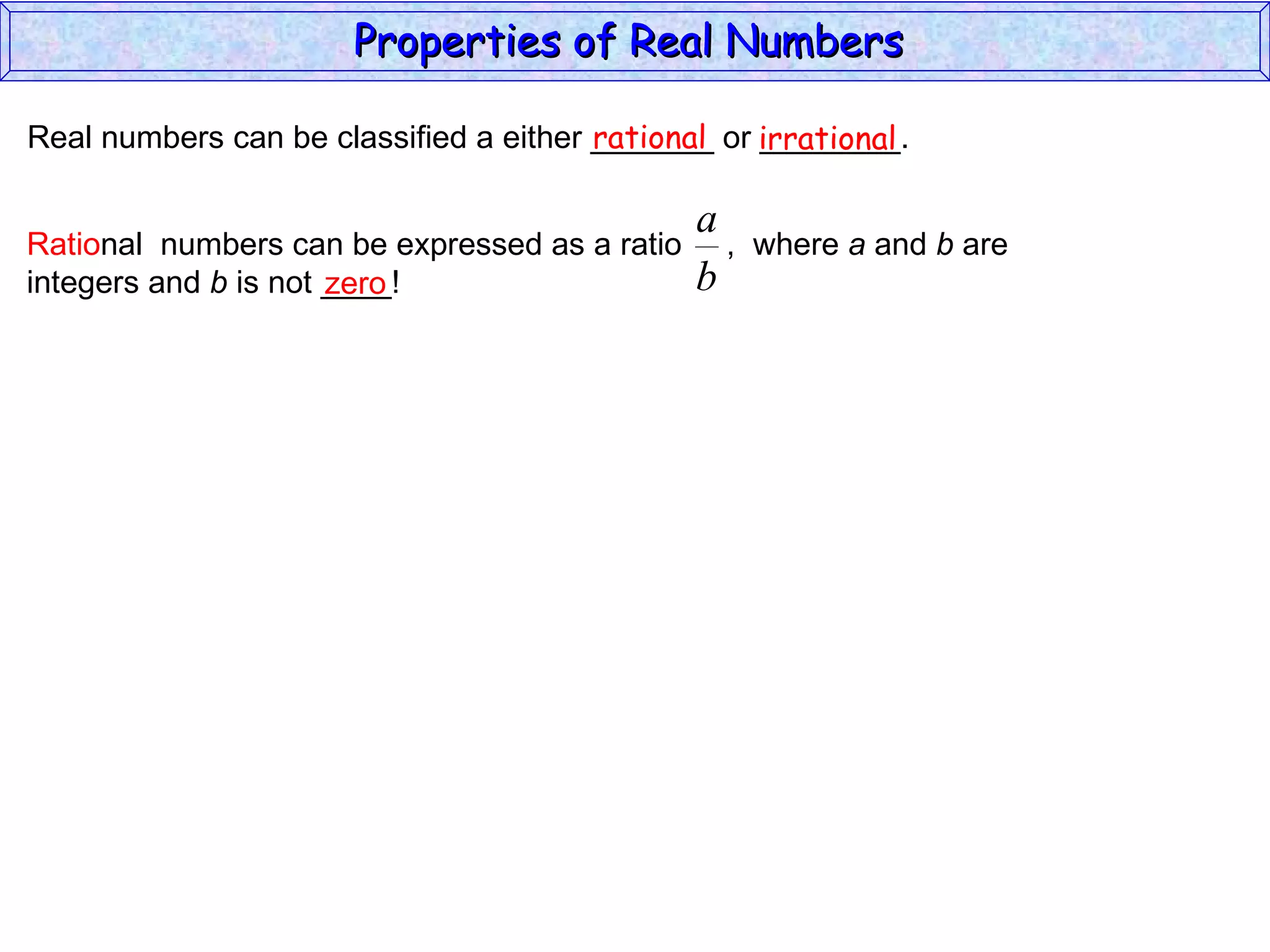
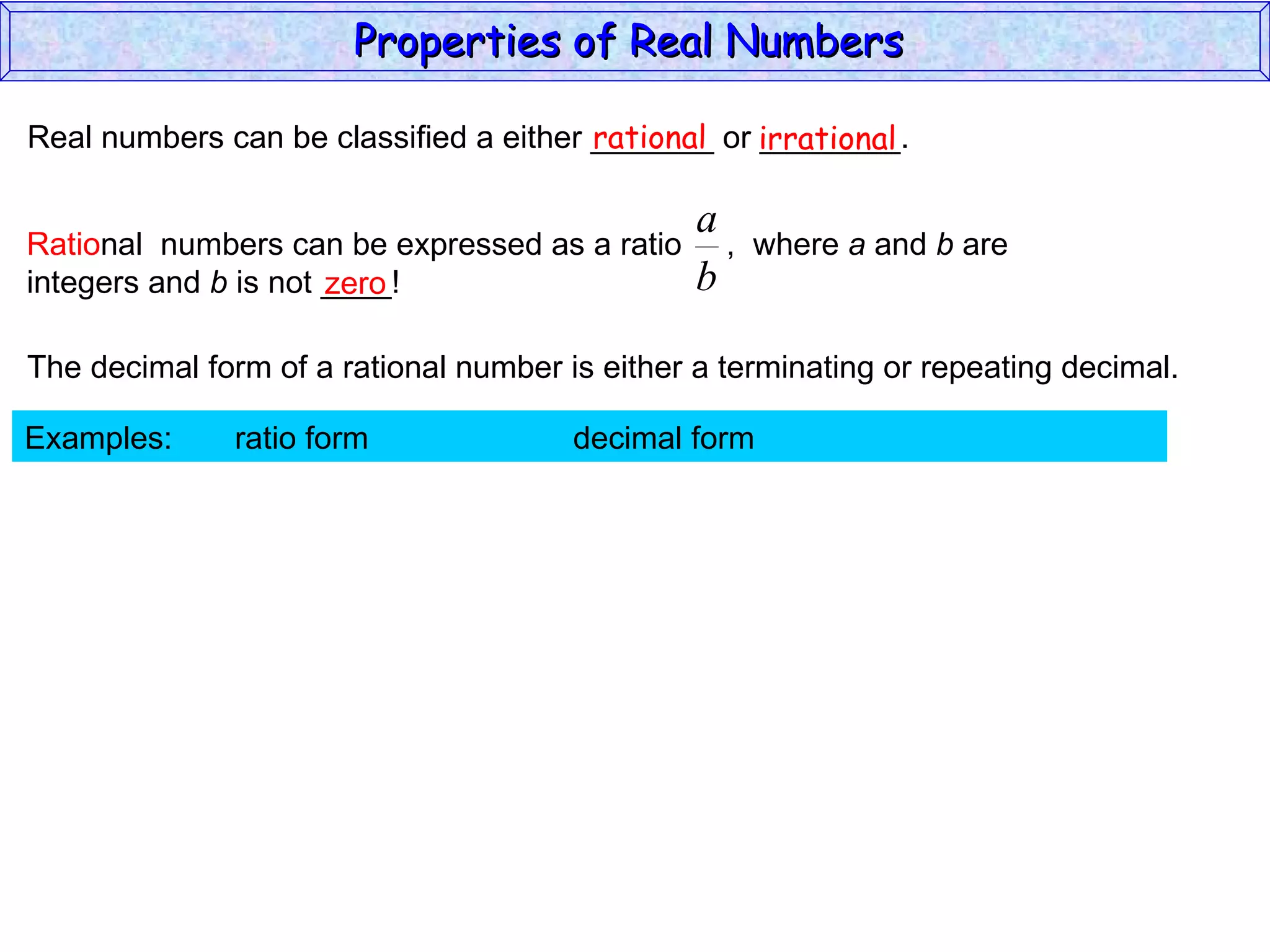
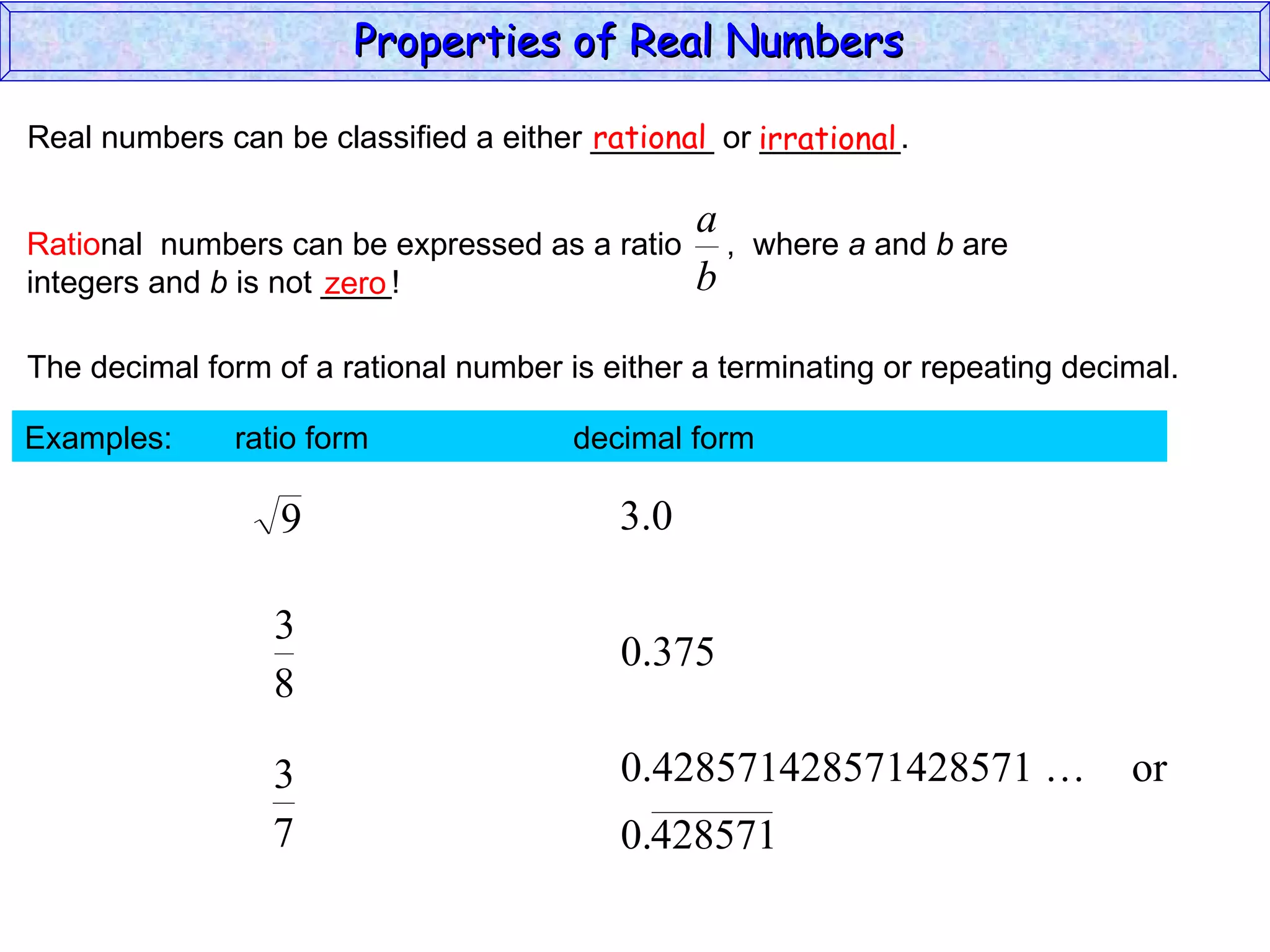
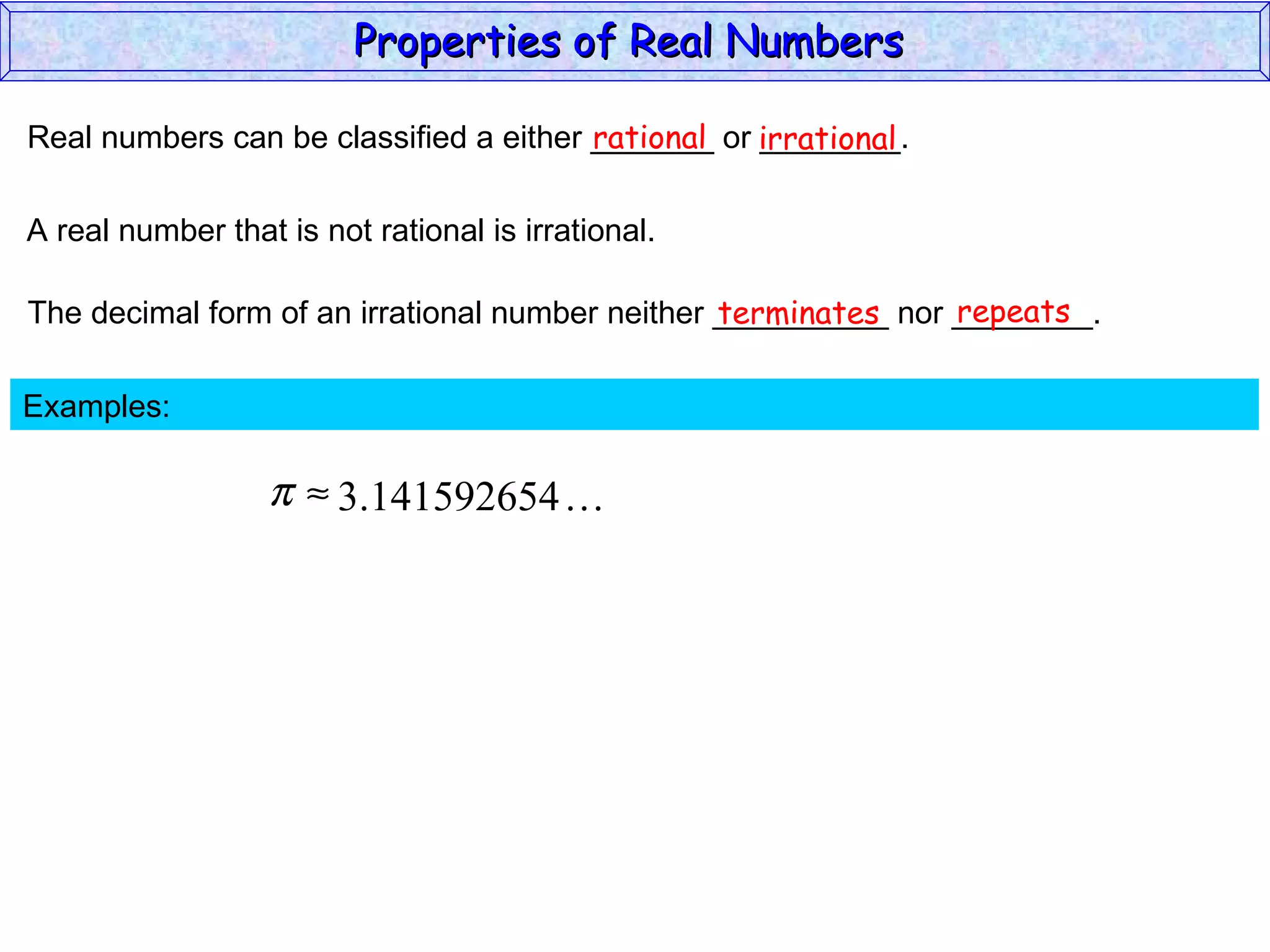
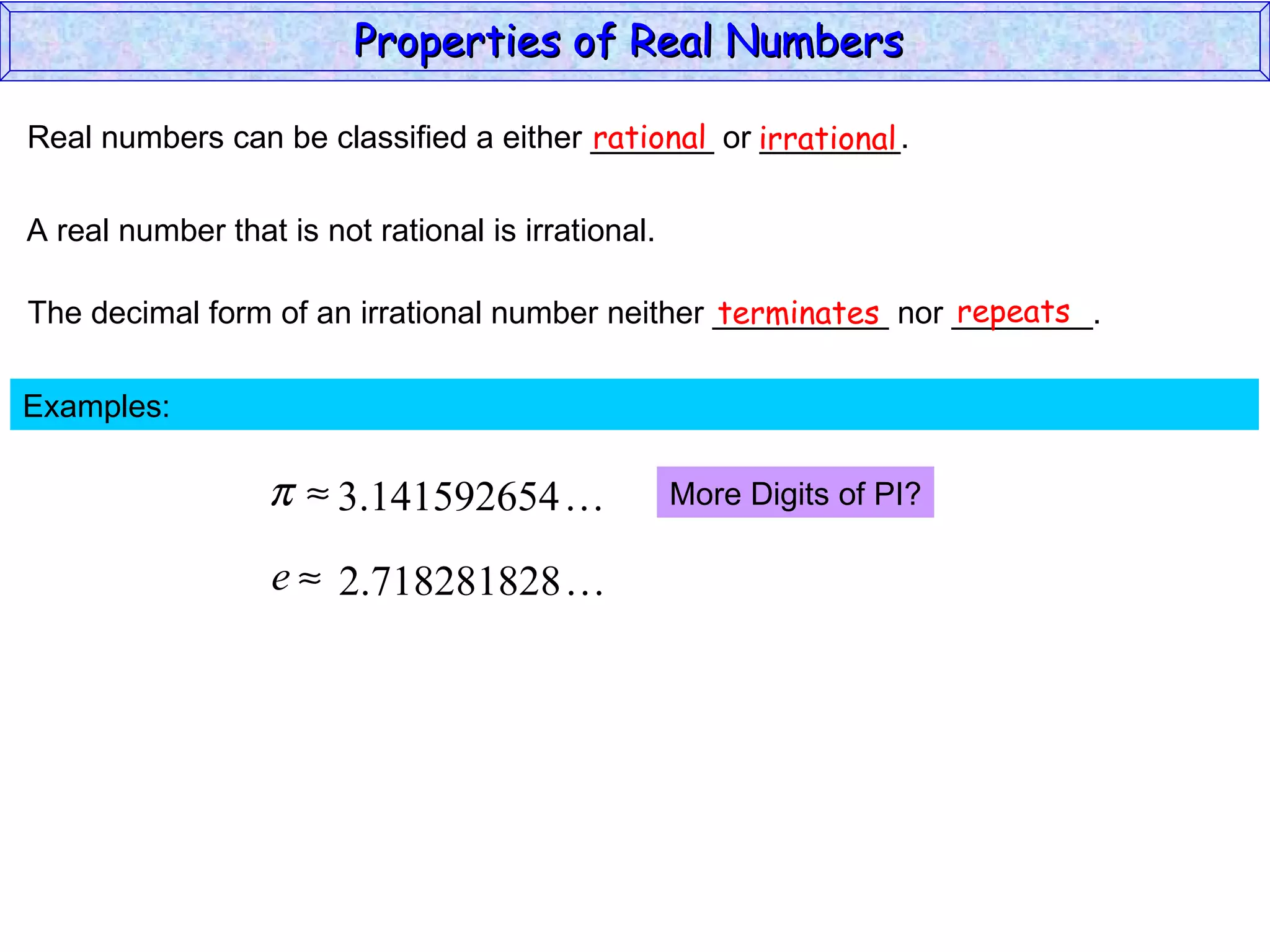
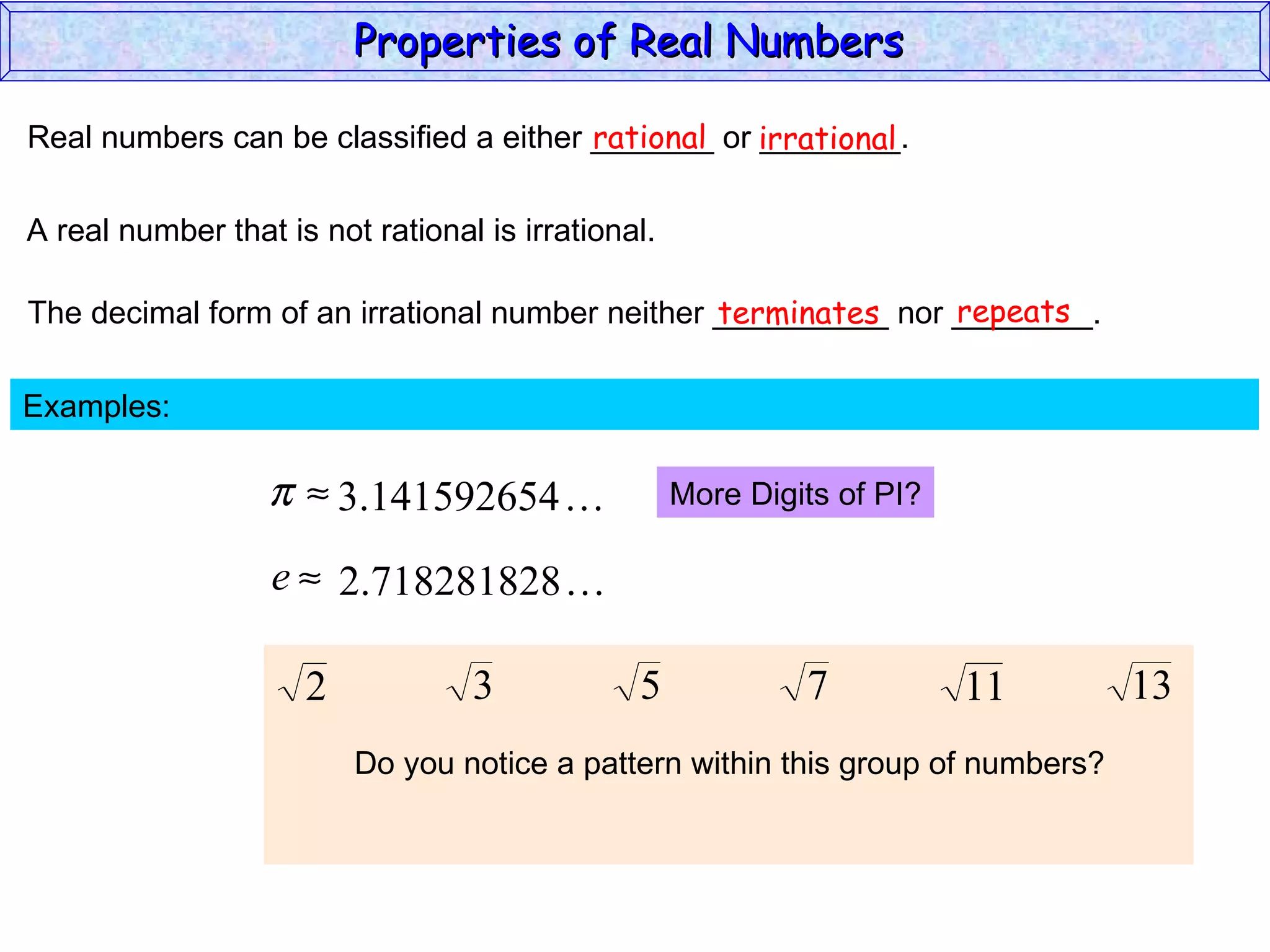
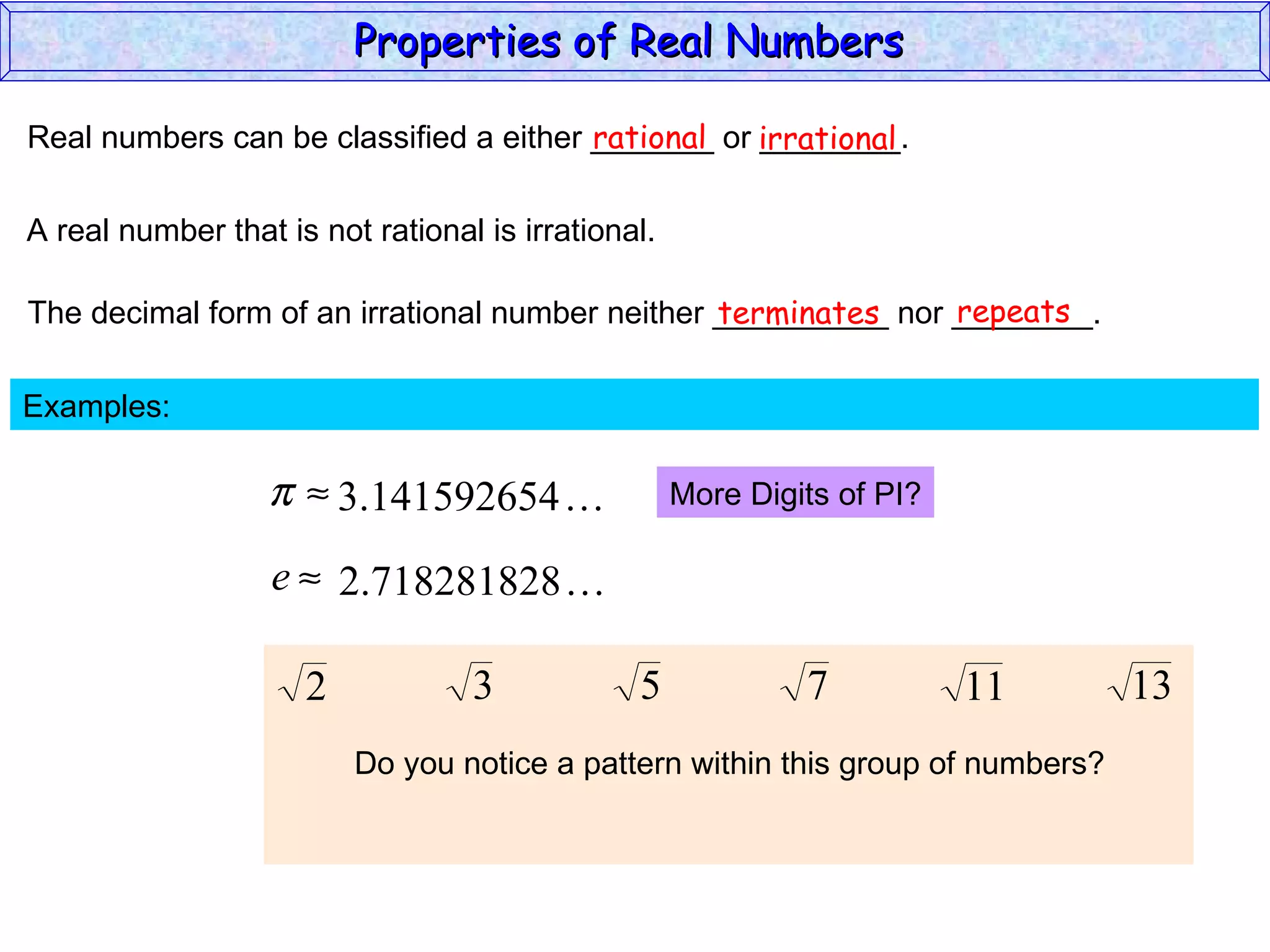
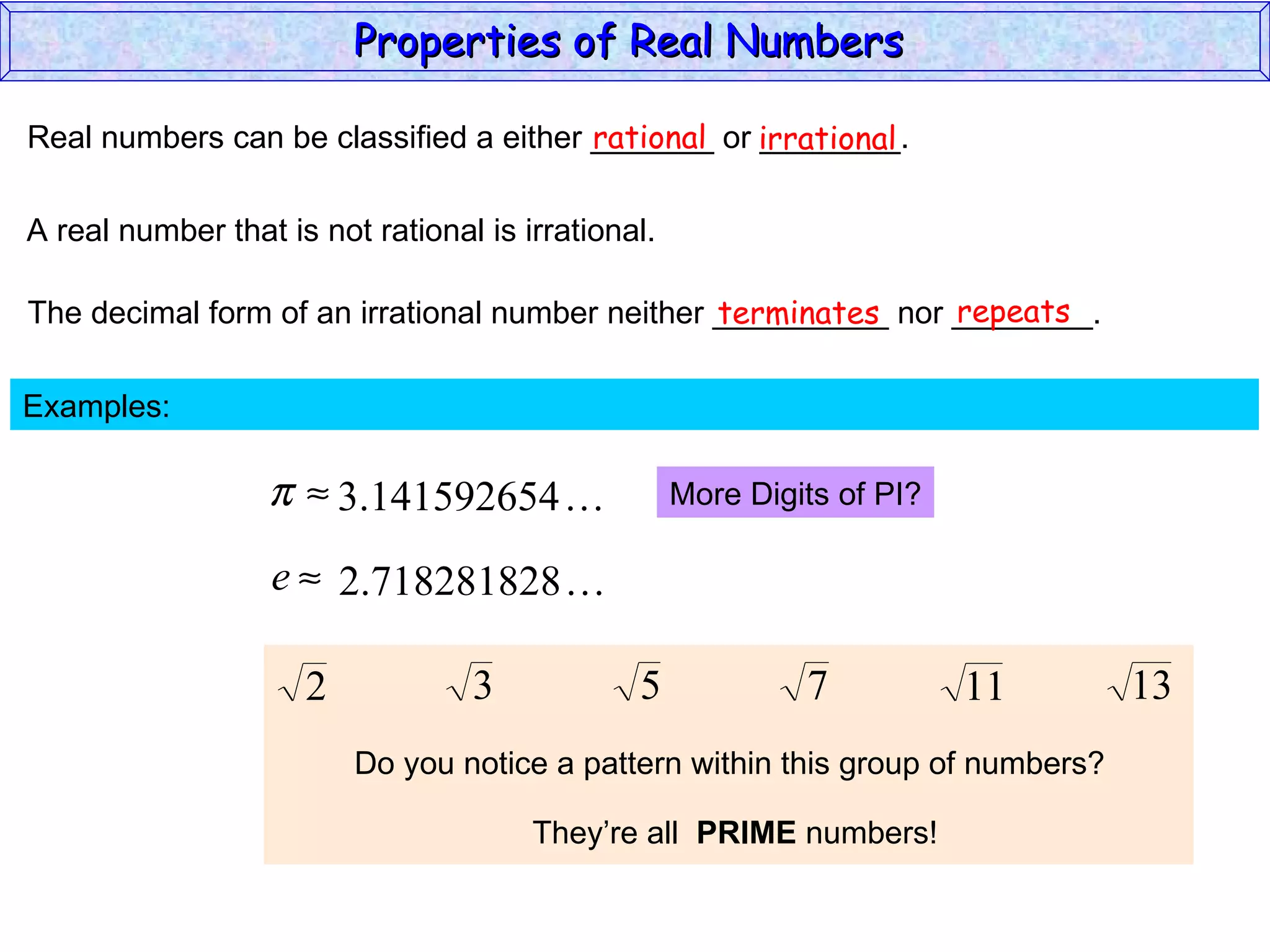
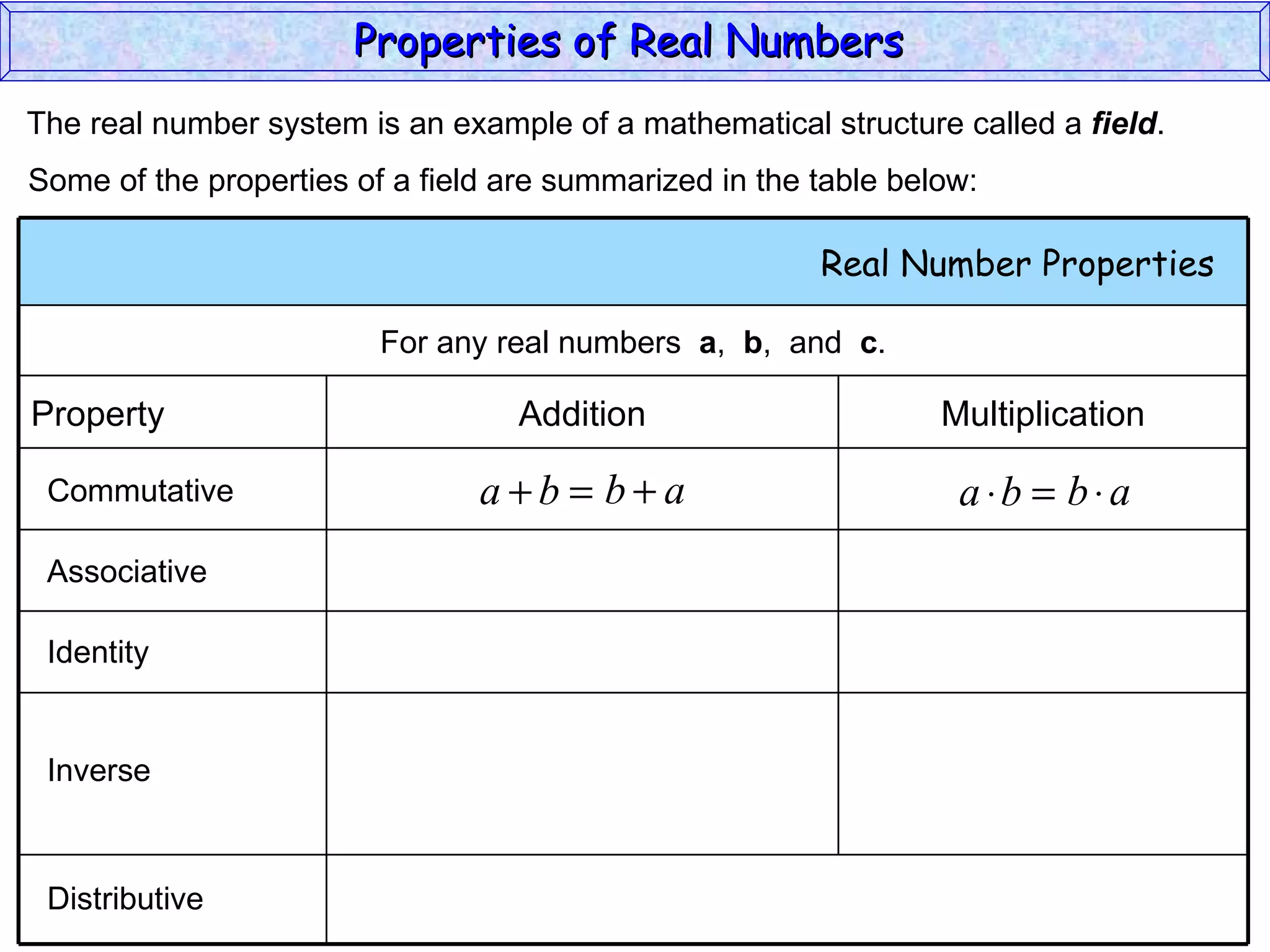
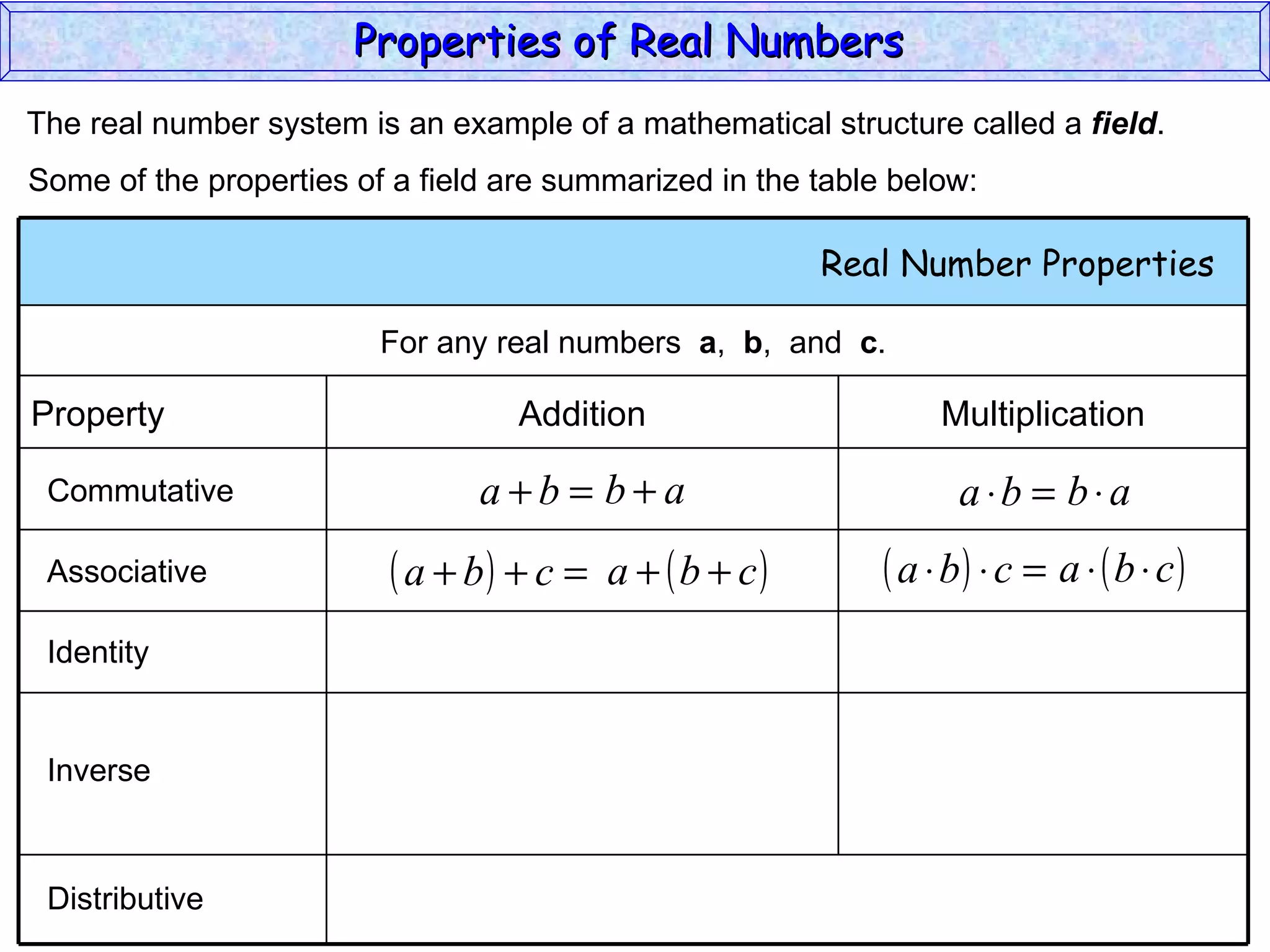
The document summarizes key properties of real numbers. It defines real, rational, and irrational numbers and discusses how they relate to each other and the number line. Rational numbers can be written as ratios of integers, and their decimals terminate or repeat. Irrational numbers have non-terminating, non-repeating decimals. The real number system forms a field with properties like commutativity and distributivity for addition and multiplication.

1. Properties of Real Numbers

2. __ __ ____ _ Properties of Real Numbers Vocabulary 1) real numbers 2) rational numbers 3) irrational numbers Classify real numbers. Use the properties of real numbers to evaluate expressions.

3. All of the numbers that you use in everyday life are real numbers . Properties of Real Numbers

4. All of the numbers that you use in everyday life are real numbers . Each real number corresponds to exactly one point on the number line, and Properties of Real Numbers

5. All of the numbers that you use in everyday life are real numbers . Each real number corresponds to exactly one point on the number line, and Properties of Real Numbers x

6. All of the numbers that you use in everyday life are real numbers . Each real number corresponds to exactly one point on the number line, and Properties of Real Numbers x 0 1 2 3 4 5 -5 -4 -2 -1 -3

7. All of the numbers that you use in everyday life are real numbers . Each real number corresponds to exactly one point on the number line, and every point on the number line represents one real number. Properties of Real Numbers x 0 1 2 3 4 5 -5 -4 -2 -1 -3

8. All of the numbers that you use in everyday life are real numbers . Each real number corresponds to exactly one point on the number line, and every point on the number line represents one real number. Properties of Real Numbers x 0 1 2 3 4 5 -5 -4 -2 -1 -3

9. Real numbers can be classified a either _______ or ________. Properties of Real Numbers

10. Real numbers can be classified a either _______ or ________. rational irrational Properties of Real Numbers

11. Real numbers can be classified a either _______ or ________. rational irrational zero Properties of Real Numbers Ratio nal numbers can be expressed as a ratio , where a and b are integers and b is not ____!

12. Real numbers can be classified a either _______ or ________. rational irrational zero The decimal form of a rational number is either a terminating or repeating decimal. Properties of Real Numbers Ratio nal numbers can be expressed as a ratio , where a and b are integers and b is not ____!

13. Real numbers can be classified a either _______ or ________. rational irrational zero The decimal form of a rational number is either a terminating or repeating decimal. Examples: ratio form decimal form Properties of Real Numbers Ratio nal numbers can be expressed as a ratio , where a and b are integers and b is not ____!

14. Real numbers can be classified a either _______ or ________. rational irrational zero The decimal form of a rational number is either a terminating or repeating decimal. Examples: ratio form decimal form Properties of Real Numbers Ratio nal numbers can be expressed as a ratio , where a and b are integers and b is not ____!

15. Real numbers can be classified a either _______ or ________. rational irrational zero The decimal form of a rational number is either a terminating or repeating decimal. Examples: ratio form decimal form Properties of Real Numbers Ratio nal numbers can be expressed as a ratio , where a and b are integers and b is not ____!

16. Real numbers can be classified a either _______ or ________. rational irrational zero The decimal form of a rational number is either a terminating or repeating decimal. Examples: ratio form decimal form Properties of Real Numbers Ratio nal numbers can be expressed as a ratio , where a and b are integers and b is not ____!

17. Real numbers can be classified a either _______ or ________. rational irrational A real number that is not rational is irrational. Properties of Real Numbers

18. Real numbers can be classified a either _______ or ________. rational irrational A real number that is not rational is irrational. The decimal form of an irrational number neither __________ nor ________. Properties of Real Numbers

19. Real numbers can be classified a either _______ or ________. rational irrational A real number that is not rational is irrational. The decimal form of an irrational number neither __________ nor ________. terminates repeats Properties of Real Numbers

20. Real numbers can be classified a either _______ or ________. rational irrational A real number that is not rational is irrational. The decimal form of an irrational number neither __________ nor ________. terminates repeats Examples: Properties of Real Numbers

21. Real numbers can be classified a either _______ or ________. rational irrational A real number that is not rational is irrational. The decimal form of an irrational number neither __________ nor ________. terminates repeats Examples: More Digits of PI? Properties of Real Numbers

22. Real numbers can be classified a either _______ or ________. rational irrational A real number that is not rational is irrational. The decimal form of an irrational number neither __________ nor ________. terminates repeats Examples: More Digits of PI? Do you notice a pattern within this group of numbers? Properties of Real Numbers

23. Real numbers can be classified a either _______ or ________. rational irrational A real number that is not rational is irrational. The decimal form of an irrational number neither __________ nor ________. terminates repeats Examples: More Digits of PI? Do you notice a pattern within this group of numbers? Properties of Real Numbers

24. Real numbers can be classified a either _______ or ________. rational irrational A real number that is not rational is irrational. The decimal form of an irrational number neither __________ nor ________. terminates repeats Examples: More Digits of PI? Do you notice a pattern within this group of numbers? They’re all PRIME numbers! Properties of Real Numbers

25. Relationships among the real numbers - ( sets and subsets ). Properties of Real Numbers

26. Q = rationals I = irrationals Relationships among the real numbers - ( sets and subsets ). Properties of Real Numbers Q I

27. Q = rationals I = irrationals Z = integers Relationships among the real numbers - ( sets and subsets ). Properties of Real Numbers Q I Z

28. Q = rationals I = irrationals Z = integers W = wholes Relationships among the real numbers - ( sets and subsets ). Properties of Real Numbers Q I Z W

29. The square root of any whole number is either whole or irrational. Properties of Real Numbers

30. The square root of any whole number is either whole or irrational. Properties of Real Numbers For example, is a whole number, but , since it lies between 5 and 6, must be irrational.

31. The square root of any whole number is either whole or irrational. Properties of Real Numbers x 0 1 3 2 4 5 6 7 9 8 10 For example, is a whole number, but , since it lies between 5 and 6, must be irrational.

32. The square root of any whole number is either whole or irrational. Common Misconception: Do not assume that a number is irrational just because it is expressed using the square root symbol. Find its value first! Properties of Real Numbers x 0 1 3 2 4 5 6 7 9 8 10 For example, is a whole number, but , since it lies between 5 and 6, must be irrational.

33. The square root of any whole number is either whole or irrational. Common Misconception: Do not assume that a number is irrational just because it is expressed using the square root symbol. Find its value first! Study Tip: KNOW and recognize (at least) these numbers, Properties of Real Numbers x 0 1 3 2 4 5 6 7 9 8 10 For example, is a whole number, but , since it lies between 5 and 6, must be irrational.

34. The real number system is an example of a mathematical structure called a field . Some of the properties of a field are summarized in the table below: Properties of Real Numbers

35. The real number system is an example of a mathematical structure called a field . Some of the properties of a field are summarized in the table below: Associative Identity Inverse Distributive Properties of Real Numbers Commutative Real Number Properties For any real numbers a , b , and c . Property Addition Multiplication

36. The real number system is an example of a mathematical structure called a field . Some of the properties of a field are summarized in the table below: Commutative Associative Identity Inverse Distributive Properties of Real Numbers Real Number Properties For any real numbers a , b , and c . Property Addition Multiplication

37. The real number system is an example of a mathematical structure called a field . Some of the properties of a field are summarized in the table below: Commutative Associative Identity Inverse Distributive Properties of Real Numbers Real Number Properties For any real numbers a , b , and c . Property Addition Multiplication

38. The real number system is an example of a mathematical structure called a field . Some of the properties of a field are summarized in the table below: Commutative Associative Identity Inverse Distributive Properties of Real Numbers Real Number Properties For any real numbers a , b , and c . Property Addition Multiplication

39. The real number system is an example of a mathematical structure called a field . Some of the properties of a field are summarized in the table below: Commutative Associative Identity Inverse Distributive Properties of Real Numbers Real Number Properties For any real numbers a , b , and c . Property Addition Multiplication

40. The real number system is an example of a mathematical structure called a field . Some of the properties of a field are summarized in the table below: Commutative Associative Identity Inverse Distributive Properties of Real Numbers Real Number Properties For any real numbers a , b , and c . Property Addition Multiplication

41. Reciprocals The Reciprocal of a is providing a does NOT equal 0. Definition of Subtraction: Adding the opposite: Definition of Division: Multiplying by the reciprocal:

42. Operations with Real Numbers A. The sum of -5 and -13 is The difference of -17 and -8 is C. The product of -3 and -6 is D. The quotient of 28 and -7 is

43. Real Life Wind Farms One barrel of oil can generate 545 kilowatt-hours of electricity. In 1990, the 17,000 windmills in California could generate up to 1.5 million kilowatt-hours per hour. At peak capacity, how many barrels of oil could be saved each hour? Operating at 75% of peak efficiency, how many barrels of oil could be saved in a year?

44. At 75% peak capacity for a year

45. Consider these Java Applets to better understand the Distributive Property Algebra Tiles 1 Algebra Tiles 2 End of Lesson