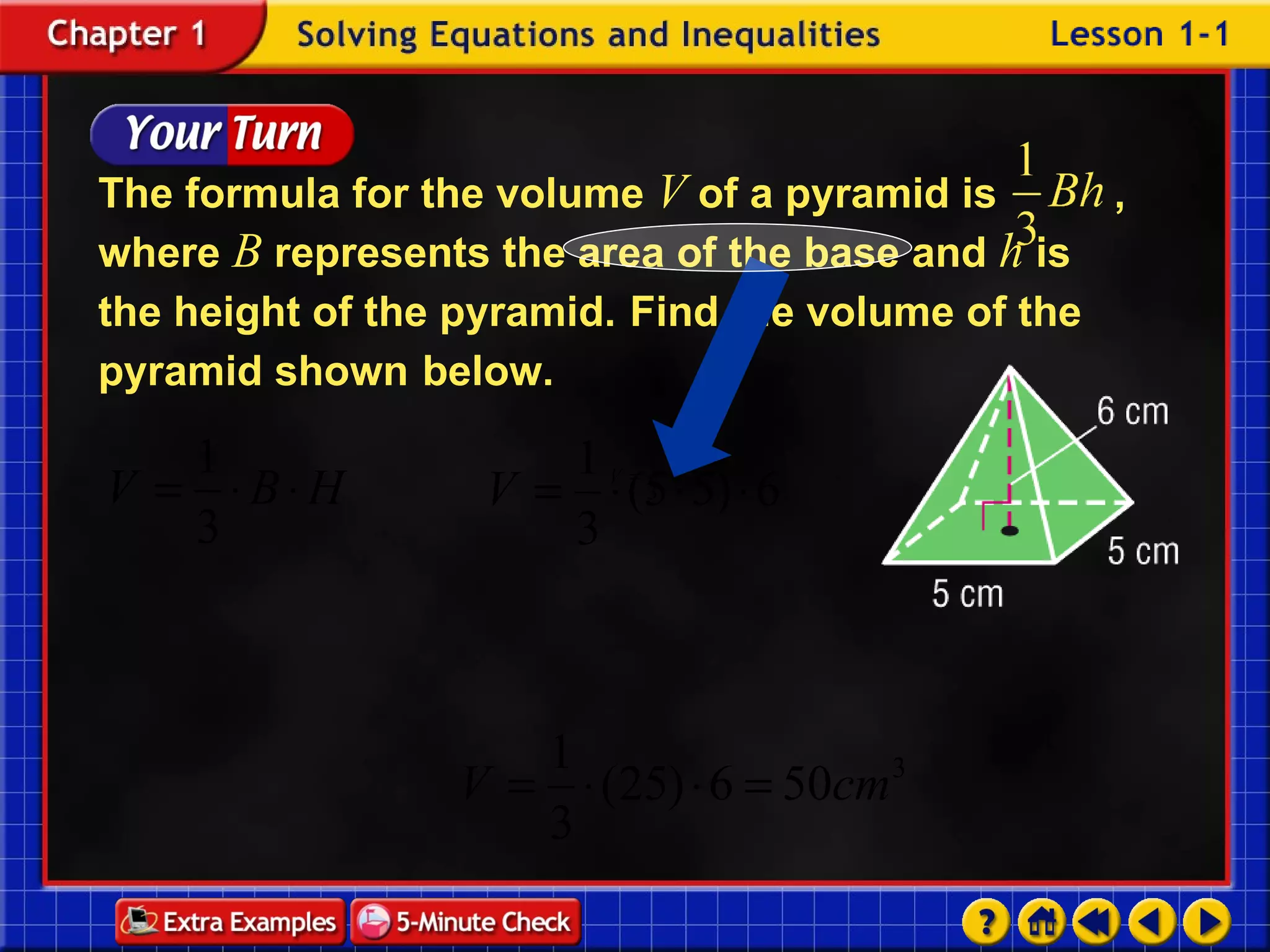
1. The document discusses simplifying algebraic expressions by identifying parts such as terms, coefficients, and constants. It also covers combining like terms. 2. It explains the order of operations as PEMDAS and uses it to evaluate expressions. Parentheses have the highest priority, then exponents, multiplication, division, addition and subtraction from left to right. 3. Formulas are mathematical relationships between quantities that can be used to find unknown values. Examples of using formulas to find the area of geometric shapes are provided.

1. 1-2: Simplifying Algebraic Expressions

2. IDing Parts of an Algebraic Expression Any thing separated by addition or subtraction is a TERM . A term that has NO variable is a CONSTANT . Any number that multiplies a variable is a COEFFICIENT . 7a 4a 3b 6 + + - 7a 4a 3b 6 + + - 7 a 4 a 3 b 6 + + -

3. Parts of an Algebraic Expression/ Combining Like Terms Terms that have identical variables and exponents are LIKE TERMS . To SIMPLIFY Expressions with Like Terms, add or subtract them. If there are NO Like Terms, then you cannot simplify any more. 7a 4a 3b 6 + + - 8c² 4a -2c³ 9 + + +

18. Example 1-4a Find the area of a trapezoid with base lengths of 13 meters and 25 meters and a height of 8 meters. Answer: The area of the trapezoid is 152 square meters. Add 13 and 25 . Area of a trapezoid Replace h with 8 , b 1 with 13 , and b 2 with 25 . Multiply 4 and 38 . Multiply 8 by .

19. Example 1-4b The formula for the volume V of a pyramid is , where B represents the area of the base and h is the height of the pyramid. Find the volume of the pyramid shown below.

20. Warm-Up Write an algebraic expression for each of the following. 5 minutes 1) twice the number n 2) half of the number n 3) 5 more than a number 4) Arthur is two years younger than Chan. Arthur is 21. How old is Chan? Translate to an equation and solve.

22. Example 1 Write as an algebraic expression. a) 3 times a number, plus 5 3n + 5 b) 12 less than the quantity 4 times a number 4n - 12 c) 8 less than half a number - 8

23. Practice 1) 3 less than twice a number Write as an algebraic expression. 2) half the difference of a number and 1 3) 4 times the quantity 3 greater than a number 4) 2 fewer than the product of 10 and a number

24. Example 2 This week Belinda worked 3 more than twice as many hours as last week. Let h be the hours worked last week. Write an expression for the hours worked this week. 2h + 3

25. Example 3 The depth of the new well is 4ft less than three times the depth of the old well. Let w be the depth of the old well. Write an expression for the depth of the new well. 3w - 4

26. Practice This year Todd sold five fewer houses than twice as many as he sold last year. Let n represent the number he sold last year. Write an expression of the number of houses that Todd sold this year. Translate to an equation.

27. Example 4 A rectangular garden is 40ft longer than it is wide. The total length of the fence that surrounds the garden is 1000ft. How wide is the garden? Let w be the width of the garden. 4w + 80 = 1000 -80 -80 4w = 920 4 4 w = 230 Then w + 40 is the length of the garden.

28. Example 5 On a committee of 18 persons, there were four more women than men. How many men were on the committee? Let m be the # of men on the committee m + (m + 4) = 18 2m + 4 = 18 -4 -4 2m = 14 2 2 m = 7 There were 7 men on the committee. Then m + 4 is the # of women on the committee