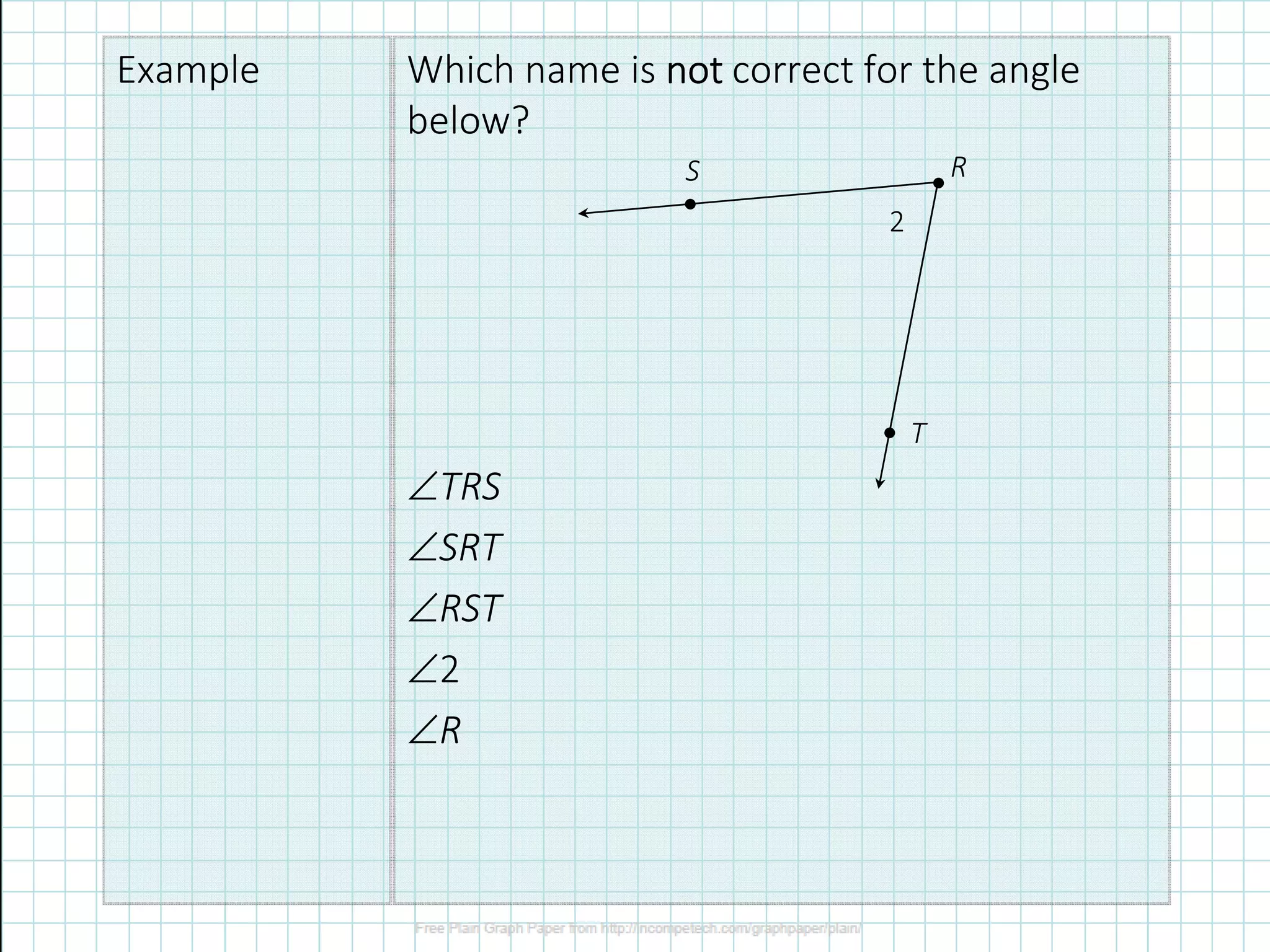
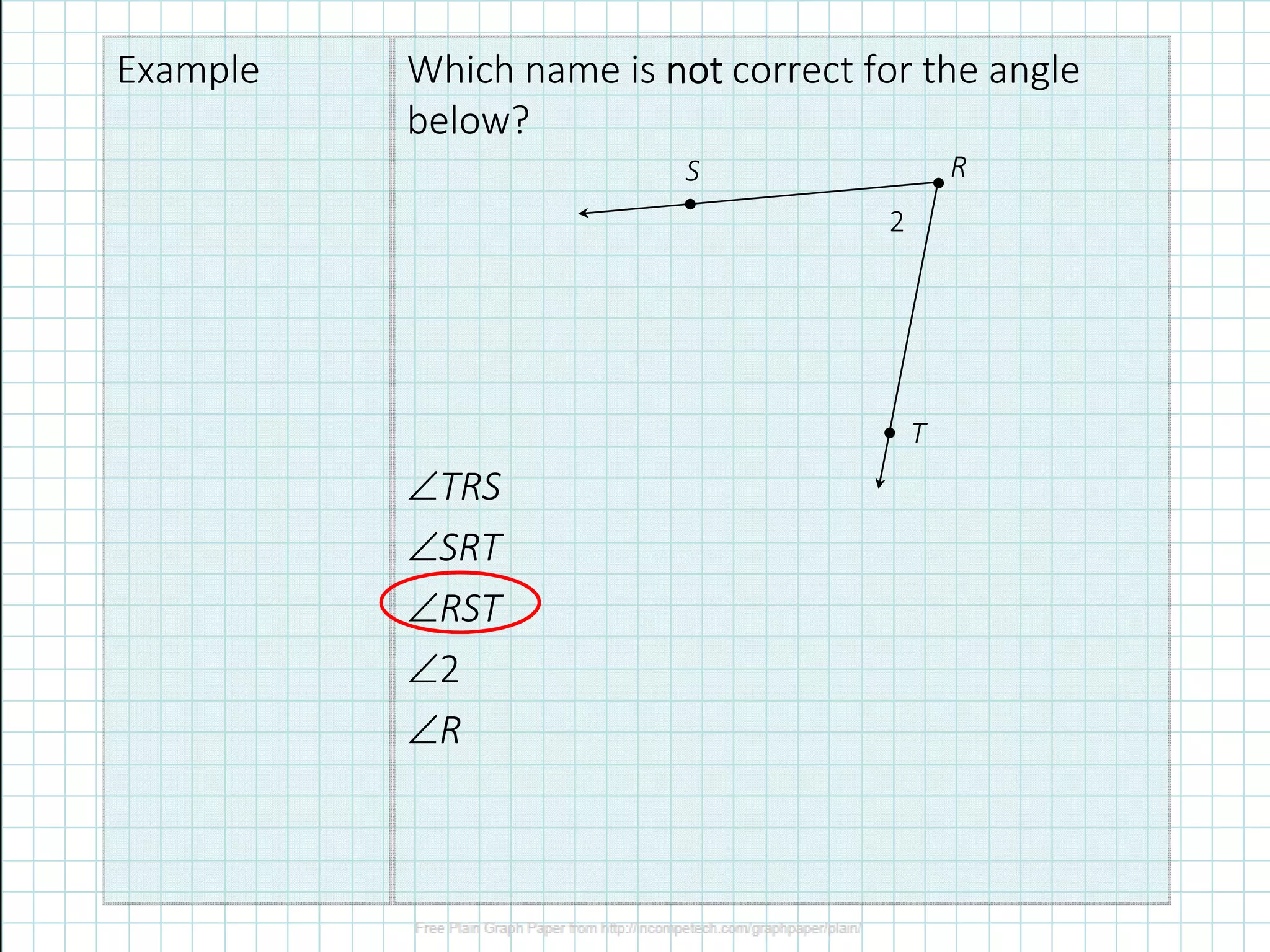
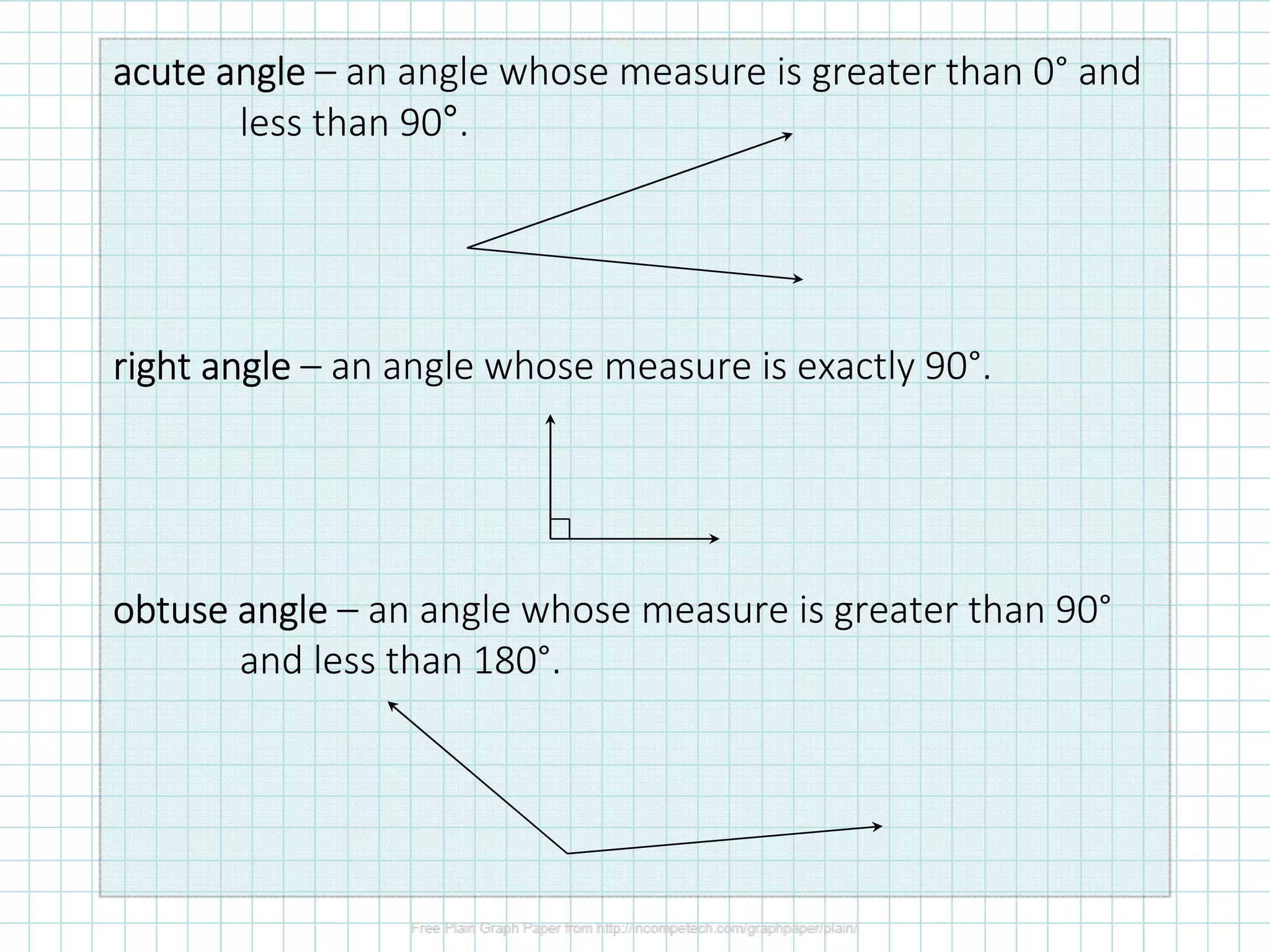
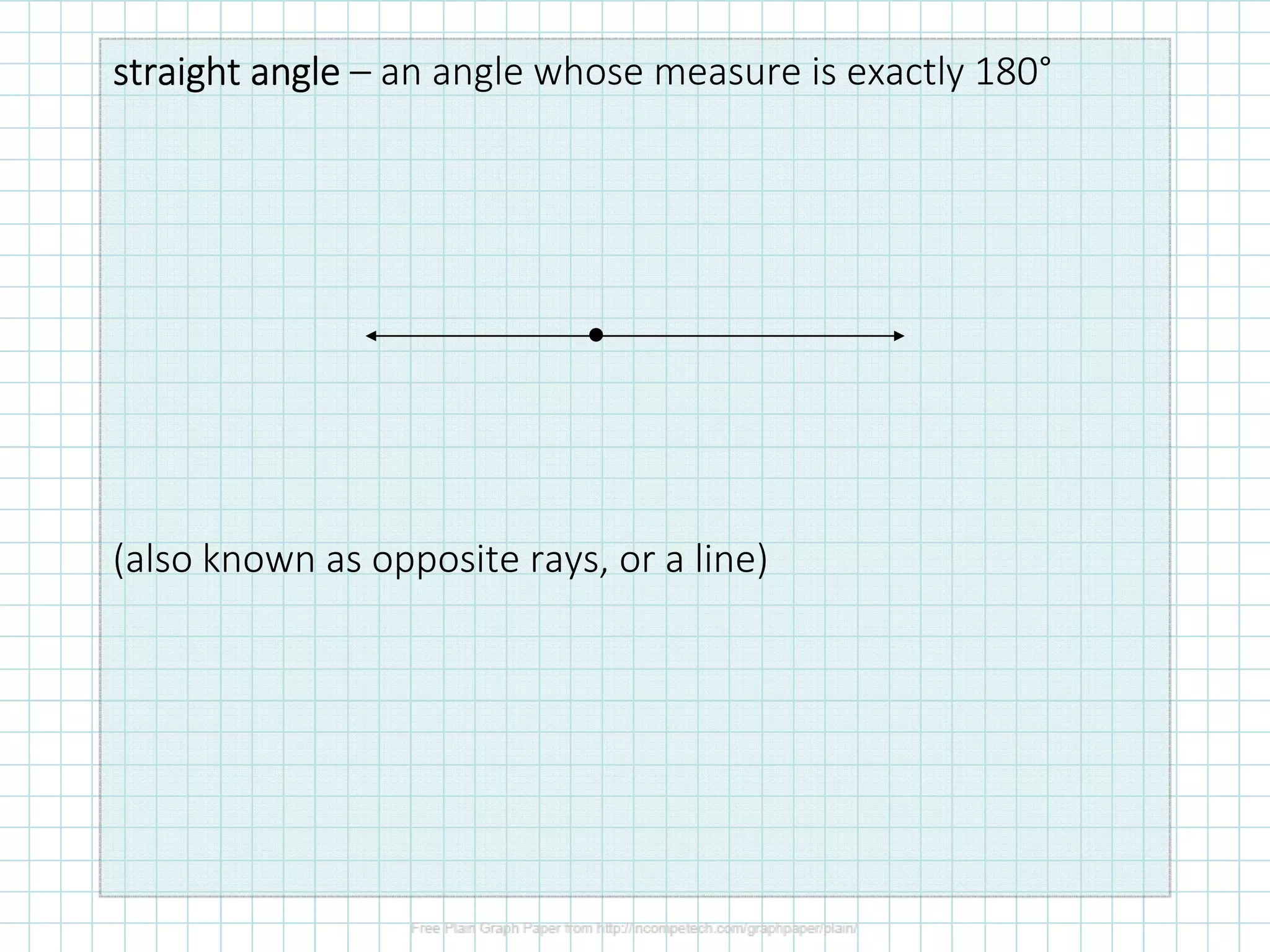
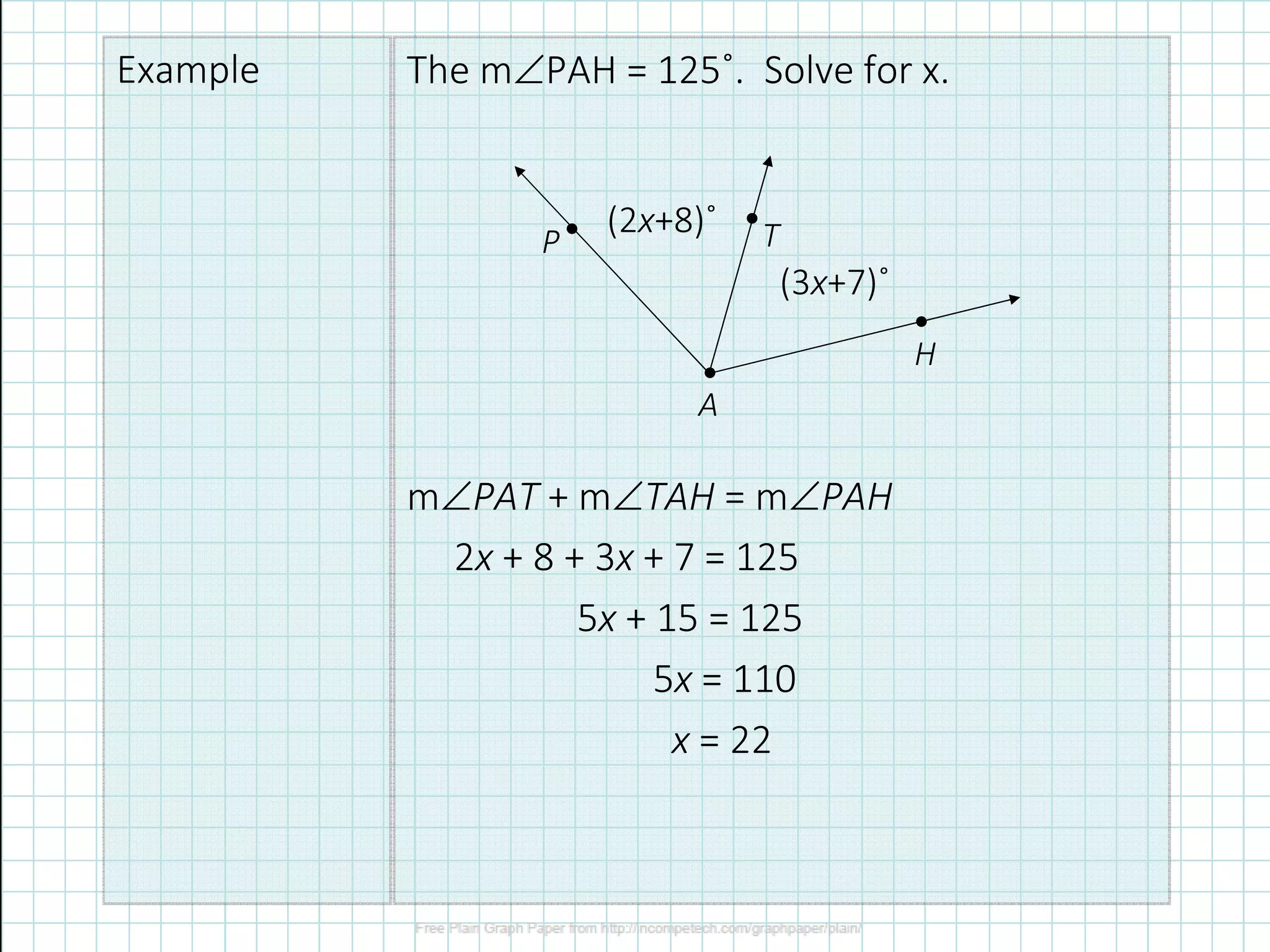
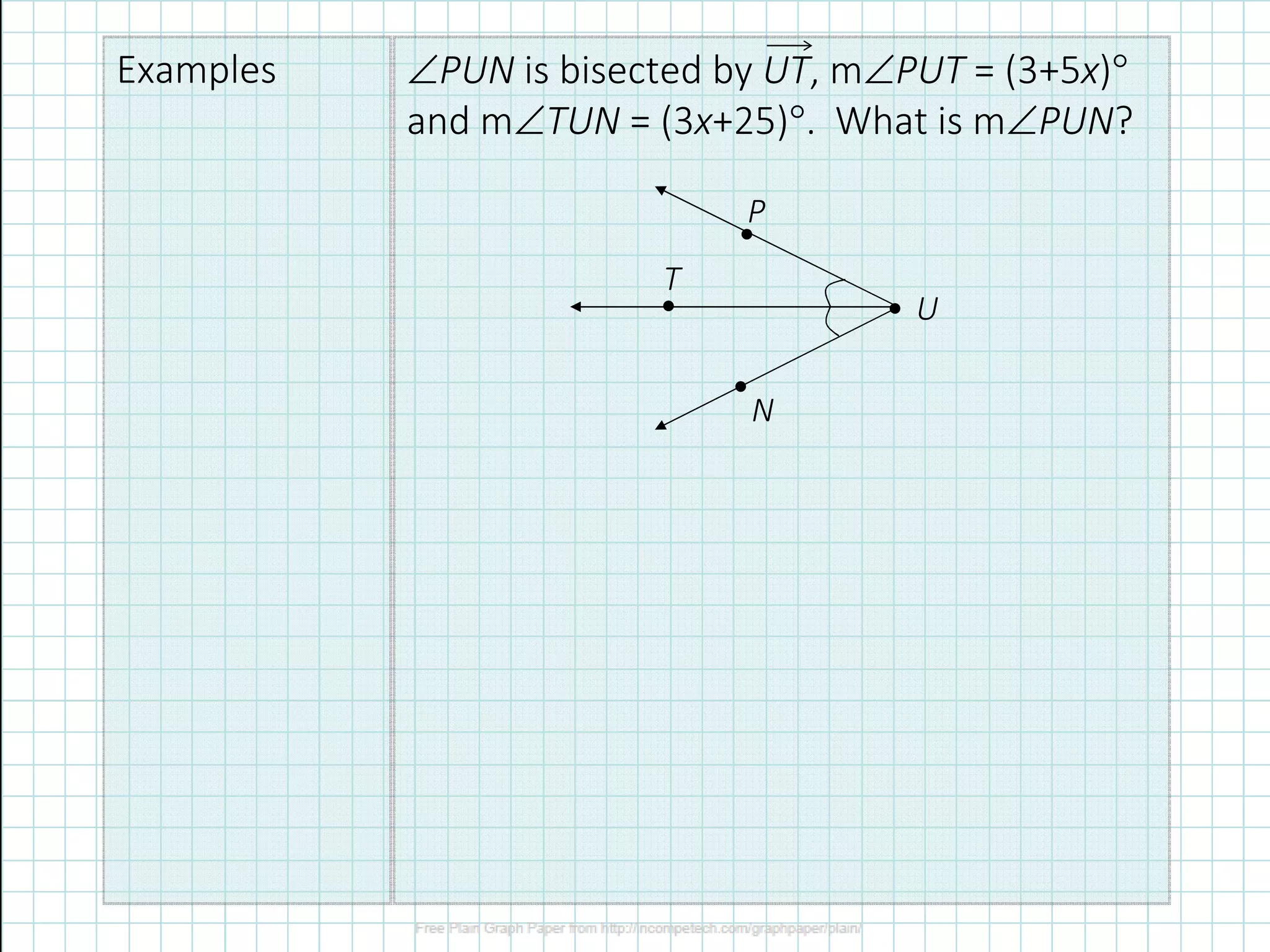
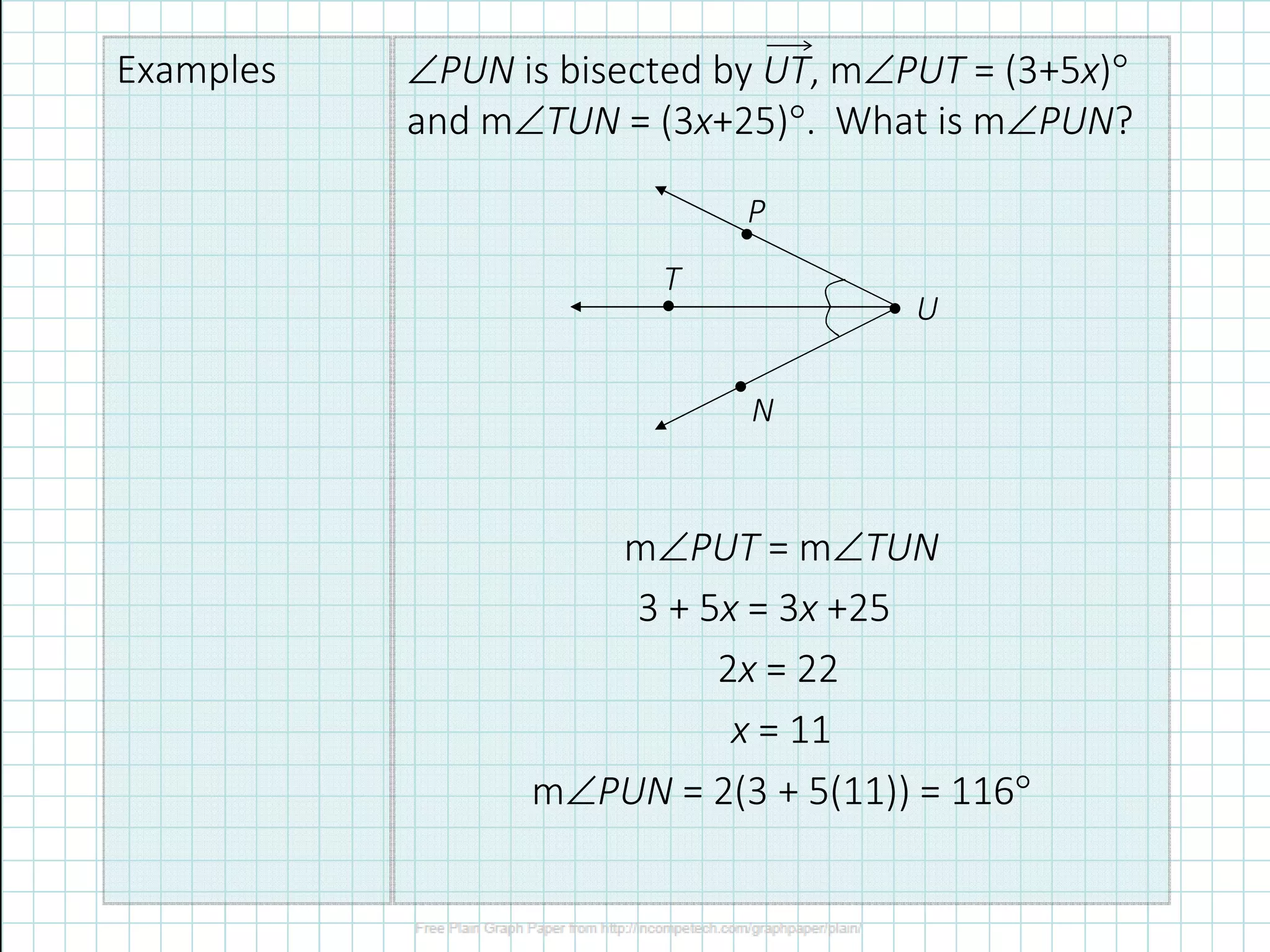
1) The document defines different types of angles (acute, right, obtuse) and angle terminology (vertex, rays). 2) It describes how to name angles and measure them in degrees. 3) Rules for adding angles and using the angle addition postulate are provided along with examples of solving for unknown angles.

1. Naming and Measuring Angles
The student will be able to (I can):
• Correctly name an angle
• Classify angles as acute, right, or obtuse
• Use the Angle Addition Postulate to solve problems• Use the Angle Addition Postulate to solve problems

2. angleangleangleangle – a figure formed by two rays or sides with a common
endpoint.
Example:
vertexvertexvertexvertex – the common endpoint of two rays or sides (plural:
●
●
A
C
R
vertexvertexvertexvertex – the common endpoint of two rays or sides (plural:
vertices).
Example: A is the vertex of the above angle

3. Notation: An angle is named one of three different ways:
1. By the vertex and a point on each ray (vertex must be in
the middle) : TEA or AET
2. By its vertex (if only one angle): E
●
●
● E
T
A
1
2. By its vertex (if only one angle): E
3. By a number: 1
Methods 1 and 3 are always correct. Method 2 can only be
used if there is only one angle at that vertex.

4. Example Which name is notnotnotnot correct for the angle
below?
TRS
●
●
●
S R
T
2
TRS
SRT
RST
2
R

5. Example Which name is notnotnotnot correct for the angle
below?
TRS
●
●
●
S R
T
2
TRS
SRT
RST
2
R

6. acuteacuteacuteacute angleangleangleangle – an angle whose measure is greater than 0° and
less than 90°.
rightrightrightright angleangleangleangle – an angle whose measure is exactly 90°.
obtuseobtuseobtuseobtuse angleangleangleangle – an angle whose measure is greater than 90°
and less than 180°.

7. straightstraightstraightstraight angleangleangleangle – an angle whose measure is exactly 180°
●
(also known as opposite rays, or a line)

8. congruentcongruentcongruentcongruent anglesanglesanglesangles – angles that have the same measure.
mWIN = mLHS
WIN  LHS
●●
●
● ●
●
L
H
S
W
IN
mWIN is read “the
measure of angle WIN”
WIN  LHS
Notation: “Arc marks” indicate congruent angles.
Notation: To write the measure of an angle, put a lowercase
“m” in front of the angle bracket.
measure of angle WIN”

9. interior of aninterior of aninterior of aninterior of an angleangleangleangle – the set of all points between the sides
of an angle
Angle AdditionAngle AdditionAngle AdditionAngle Addition PostulatePostulatePostulatePostulate:
If D is in the interiorinteriorinteriorinterior of ABC, then
mABD + mDBC = mABC (part + part = whole)
Example: If mABD=50˚ and mABC=110˚, then
mDBC=60˚
●
●●
●
A
B
D
C

10. Example The mPAH = 125˚. Solve for x.
●
●●
●
P
A
T
H
(3x+7)˚
(2x+8)˚

11. Example The mPAH = 125˚. Solve for x.
mPAT + mTAH = mPAH
●
●●
●
P
A
T
H
(3x+7)˚
(2x+8)˚
mPAT + mTAH = mPAH
2x + 8 + 3x + 7 = 125
5x + 15 = 125
5x = 110
x = 22

12. angleangleangleangle bisectorbisectorbisectorbisector – a ray that divides an angle into two
congruent angles.
Example:
●
●●
●
S
U
N
Y
UY bisects SUN; thus SUY  YUN
or mSUY = mYUN

13. Examples PUN is bisected by UT, mPUT = (3+5x)
and mTUN = (3x+25). What is mPUN?
●
● ●
●
P
U
N
T

14. Examples PUN is bisected by UT, mPUT = (3+5x)
and mTUN = (3x+25). What is mPUN?
●
● ●
●
P
U
N
T
mPUT = mTUN
3 + 5x = 3x +25
2x = 22
x = 11
mPUN = 2(3 + 5(11)) = 116

15. Example Point R is in the interior of NFL. If
mNFR = (7x – 1) and mRFL = (3x+23),
what value of x would make FR an angle
bisector?

16. Example Point R is in the interior of NFL. If
mNFR = (7x – 1) and mRFL = (3x+23),
what value of x would make FR an angle
bisector?
If FR is going to be an angle bisector, then
mNFR = mRFLmNFR = mRFL
7x – 1 = 3x + 23
4x = 24
x = 6
Therefore, if x = 6, then FR is an angle
bisector.