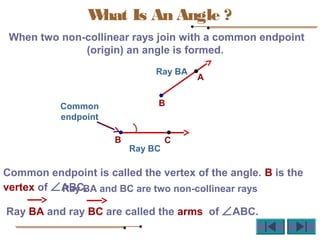
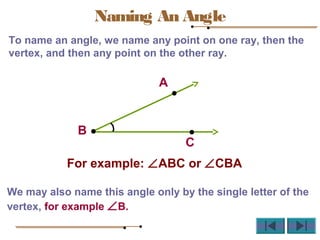
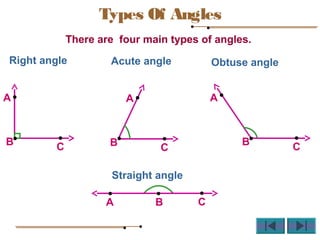
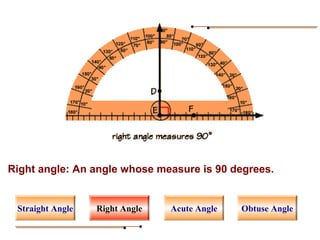
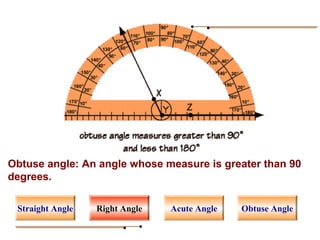
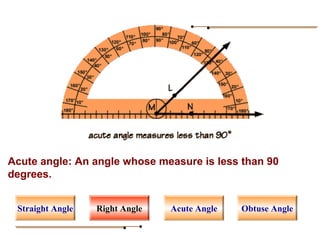
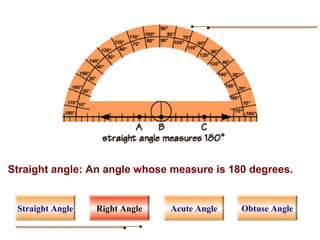
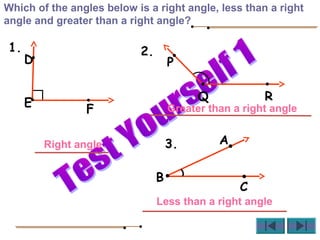
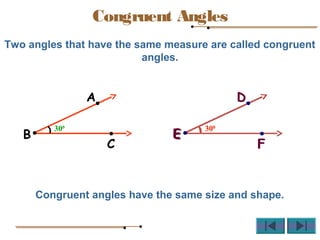
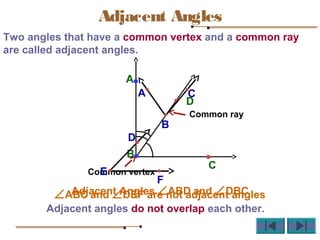
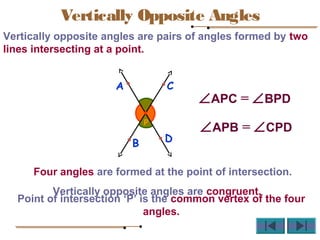
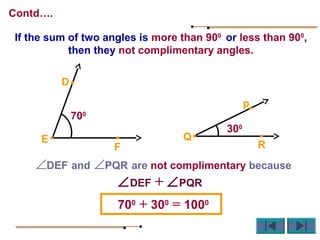
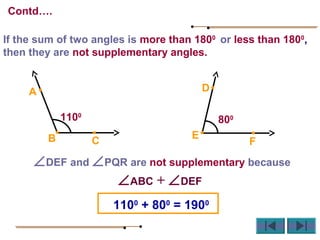
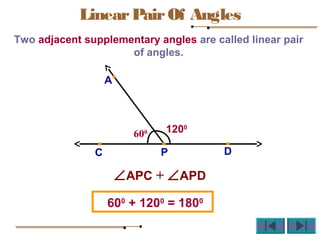
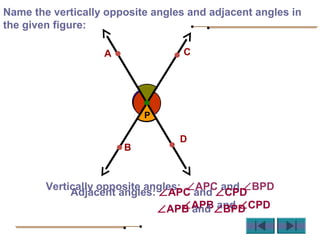
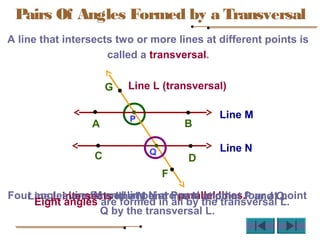
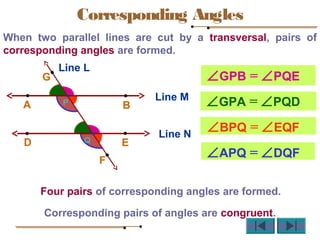
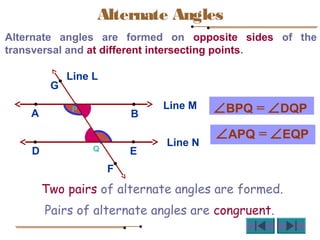
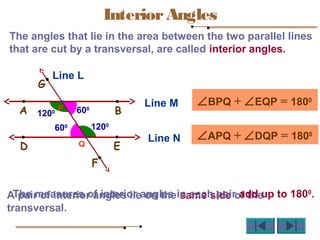
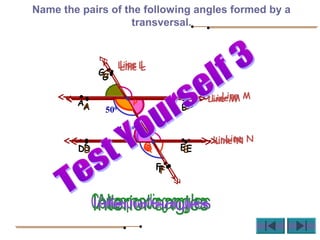
Angles are formed whenever two rays share a common endpoint. An angle can be named using the vertex point and the endpoints of the rays. There are four main types of angles: acute, obtuse, right, and straight. When lines intersect, different pairs of angles are formed including corresponding angles, alternate angles, and interior angles. Corresponding angles and alternate angles that are formed by parallel lines intersected by a transversal are congruent. The measures of interior angles on the same side of the transversal sum to 180 degrees.

1. What’s your angle?

2. Contents
• Recap the terms
• Angles in daily life
• What is an angle?
• Naming an angle
• Interior and exterior of an angle
• Measurement of angle
• Types of angle: Right angle
Obtuse angle
Acute angle
Straight angle
• Test Yourself - 1
• Congruent angles
• Pairs of angles: Types
• Test Yourself - 2
• Pairs of angles formed
by a transversal
• Test Yourself - 3

3. • Imagine
• Imagine you lived in a two-dimensional world.
You could travel around, visit friends, but
nothing in your world would have height.
• You could measure distances and angles.
• You could travel fast or slow. You could go
forward, backwards or sideways. You could
move in straight lines, circles, or anything so
long as you never go up or down.
What is a Plane?

4. Point
An exact location on a plane is
called a point.
Line
Line
segment
Ray
A straight path on a plane,
extending in both directions
with no endpoints, is called a
line.
A part of a line that has two
endpoints and thus has a
definite length is called a line
segment.
A line segment extended
indefinitely in one direction
is called a ray.
Recap Geometrical Terms

5. If we look around us, we will see angles everywhere.
Angles In Daily Life

6. Common
endpoint
B C
B
A
Ray BC
Ray BA
Ray BA and BC are two non-collinear rays
When two non-collinear rays join with a common endpoint
(origin) an angle is formed.
What Is An Angle ?
Common endpoint is called the vertex of the angle. B is the
vertex of ∠ABC.
Ray BA and ray BC are called the arms of ∠ABC.

7. Fact: We can also think of an angle formed by rotating one
ray away from its initial position.

8. To name an angle, we name any point on one ray, then the
vertex, and then any point on the other ray.
For example: ∠ABC or ∠CBA
We may also name this angle only by the single letter of the
vertex, for example ∠B.
A
B
C
Naming An Angle

9. An angle divides the points on the plane into three regions:
A
B
C
F
R
P
T
X
InteriorAnd ExteriorOf An Angle
• Points lying on the angle
(An angle)
• Points within the angle
(Its interior portion. )
• Points outside the angle
(Its exterior portion. )

10. Angles are accurately measured in degrees.
Protractor is used to measure and draw angles.
Measurement Of An Angle

11. There are four main types of angles.
Straight angle
Right angle Acute angle Obtuse angle
A
B C
A
B C
A
B C
BA C
Types Of Angles

12. Right angle: An angle whose measure is 90 degrees.
Right Angle Acute AngleStraight Angle Obtuse Angle

13. Examples Of Right Angle

14. Obtuse angle: An angle whose measure is greater than 90
degrees.
Right Angle Acute AngleStraight Angle Obtuse Angle

15. Examples Of Obtuse Angle

16. Acute angle: An angle whose measure is less than 90
degrees.
Right Angle Acute AngleStraight Angle Obtuse Angle

17. Examples Of Acute Angle

18. Straight angle: An angle whose measure is 180 degrees.
Right Angle Acute AngleStraight Angle Obtuse Angle

19. Examples Of Straight Angle

20. A
B
C
D
E
F
P
Q R
Which of the angles below is a right angle, less than a right
angle and greater than a right angle?
Right angle
Greater than a right angle
Less than a right angle
1. 2.
3.

21. Two angles that have the same measure are called congruent
angles.
Congruent angles have the same size and shape.
A
B
C
300
D
E
F
300
D
E
F
300
Congruent Angles

22. Pairs Of Angles : Types
• Adjacent angles
• Vertically opposite angles
• Complimentary angles
• Supplementary angles
• Linear pairs of angles

23. Adjacent Angles
Two angles that have a common vertex and a common ray
are called adjacent angles.
C
D
B
A
Common ray
Common vertex
Adjacent Angles ∠ABD and ∠DBC
Adjacent angles do not overlap each other.
D
E
F
A
B
C
∠ABC and ∠DEF are not adjacent angles

24. Vertically Opposite Angles
Vertically opposite angles are pairs of angles formed by two
lines intersecting at a point.
∠APC = ∠BPD
∠APB = ∠CPD
A
DB
C
P
Four angles are formed at the point of intersection.
Point of intersection ‘P’ is the common vertex of the four
angles.
Vertically opposite angles are congruent.

25. If the sum of two angles is 900
, then they are called
complimentary angles.
600
A
B
C
300
D
E
F
∠ABC and ∠DEF are complimentary because
600
+ 300
= 900
∠ABC + ∠DEF
Complimentary Angles

26. 700
D
E
F
300
p
Q
R
If the sum of two angles is more than 900
or less than 900
,
then they not complimentary angles.
∠DEF and ∠PQR are not complimentary because
700
+ 300
= 1000
∠DEF + ∠PQR
Contd….

27. If the sum of two angles is 1800
then they are called
supplementary angles.
∠PQR and ∠ABC are supplementary, because
1000
+ 800
= 1800
RQ
P
A
B
C
1000
800
∠PQR + ∠ABC
Supplementary Angles

28. If the sum of two angles is more than 1800
or less than 1800
,
then they are not supplementary angles.
∠DEF and ∠PQR are not supplementary because
∠ABC + ∠DEF
1100
+ 800
= 1900
D
E
F
800
CB
A
1100
Contd….

29. Two adjacent supplementary angles are called linear pair
of angles.
A
600 1200
PC D
600
+ 1200
= 1800
∠APC + ∠APD
LinearPairOf Angles

30. Name the adjacent angles and linear pair of angles in the
given figure:
Adjacent angles:
∠ABD and ∠DBC
∠ABE and ∠DBA
Linear pair of angles:
∠EBA, ∠ABC C
D
B
A
E
600
300
900
∠EBD, ∠DBC
C
D
B
A
E
600
300
900

31. Name the vertically opposite angles and adjacent angles in
the given figure:
A
D
B
C
P
Vertically opposite angles: ∠APC and ∠BPD
∠APB and ∠CPD
Adjacent angles: ∠APC and ∠CPD
∠APB and ∠BPD

32. A line that intersects two or more lines at different points is
called a transversal.
Line L (transversal)
BA
Line M
Line N
DC
P
Q
G
F
Pairs Of Angles Formed by a Transversal
Line M and line N are parallel lines.Line L intersects line M and line N at point P and Q.Four angles are formed at point P and another four at point
Q by the transversal L.
Eight angles are formed in all by the transversal L.

33. Pairs Of Angles Formed by a Transversal
• Corresponding angles
• Alternate angles
• Interior angles

34. Corresponding Angles
When two parallel lines are cut by a transversal, pairs of
corresponding angles are formed.
Four pairs of corresponding angles are formed.
Corresponding pairs of angles are congruent.
∠GPB = ∠PQE
∠GPA = ∠PQD
∠BPQ = ∠EQF
∠APQ = ∠DQF
Line M
BA
Line N
D E
L
P
Q
G
F
Line L

35. Alternate Angles
Alternate angles are formed on opposite sides of the
transversal and at different intersecting points.
Line M
BA
Line N
D E
L
P
Q
G
F
Line L
∠BPQ = ∠DQP
∠APQ = ∠EQP
Pairs of alternate angles are congruent.
Two pairs of alternate angles are formed.

36. The angles that lie in the area between the two parallel lines
that are cut by a transversal, are called interior angles.
A pair of interior angles lie on the same side of the
transversal.
The measures of interior angles in each pair add up to 1800
.
InteriorAngles
Line M
BA
Line N
D E
L
P
Q
G
F
Line L
600
1200
1200
600
∠BPQ + ∠EQP = 1800
∠APQ + ∠DQP = 1800

37. Name the pairs of the following angles formed by a
transversal.
Line M
BA
Line N
D E
P
Q
G
F
Line L
Line M
BA
Line N
D E
P
Q
G
F
Line L
Line M
BA
Line N
D E
P
Q
G
F
Line L
500
1300