Downloaded 34 times
Uploaded byAHMAD SMKN 1 TULANG BAWANG TENGAH
Trigonometry smkn1 tbt
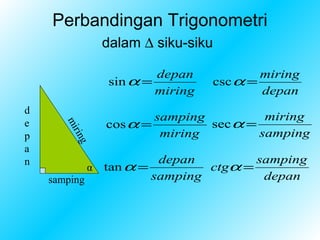
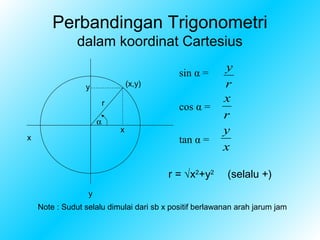
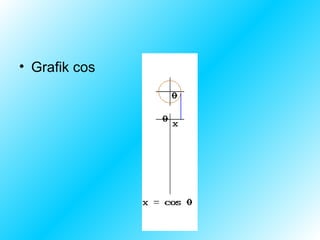
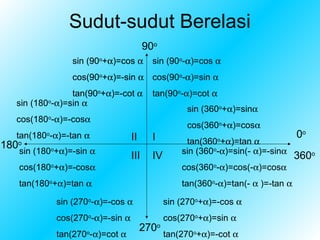
1. Dokumen membahas tentang trigonometri, terutama perbandingan trigonometri dalam segitiga siku-siku dan koordinat Cartesius, serta identitas trigonometri dasar. 2. Dijelaskan hubungan antara sin, cos, dan tan dengan sudut dan sisi-sisi segitiga, beserta tanda-tandanya tergantung kuadran. 3. Identitas trigonometri dasar seperti sin2α + cos2α = 1 dan hubungan antara sin, cos, tan, csc, sec
Trigonometry smkn1 tbt
- 1.
- 2. Perbandingan Trigonometri dalam ∆ siku-siku depan miring sin α = csc α = miring depan d samping miring e cos α = sec α = mi miring samping rin p g a n depan samping α tan α = ctgα = samping samping depan
- 3. Latihan 1 p r r sin α = sin β = q q p α r p cos α = q cos β = q q β p r tan α = tan β = r p
- 4. Segitiga Siku-Siku Istimewa sin 30o= 1/2 sin 60o= √3/2 sin 45 = 1/√2 o cos 30o= √3/2 cos 60o= 1/2 cos 45 = 1/√2 o 300 tan 30o= 1/√3 tan 60o= √3 tan 45o= 1 450 3 2 2 1 600 450 1 1 Bagaimana jika segitiganya tidak istimewa?
- 5. Latihan 2 Tentukan nilai a! √160 15 a 3a a 25o 7a 45 50o ao 30 Jawab: 10 2 70 32,17 19,47
- 6. Contoh Soal no3 • Tentukan x, k, dan h ! x 7 320 5 k h Ans :4,37 25,40 53,320 x 10 Ans :10,53 Ans :h = 13,43 k = 16.74
- 7. Sudut Elevasi danDepresi Sudut depresi mobil Sudut elevasi layang-layang
- 8. LATIHAN Kerjakan latihan darikertas fotocopy yang dibagikan hal. 2 no. 2 sampai dengan 8
- 9.
- 10. KUADRAN 900 Kuadran II : 900 < α < 1800 Kuadran I : 0 < α < 900 α 00 / 180 0 3600 Kuadran III : 1800 < α < 2700 Kuadran IV : 2700 < α < 3600 2700 Sudut + selalu dibentuk dari sumbu x+ berlawanan arah jarum jam
- 11. Perbandingan Trigonometri dalam koordinat Cartesius sin α = y y (x,y) r r x cos α = α r x y x tan α = x r = √x2+y2 (selalu +) y Note : Sudut selalu dimulai dari sb x positif berlawanan arah jarum jam
- 12. Bagaimana untuk sudut istimewa 0o dan 90o y sin 90 = o =1 r sin 0o = 0 P(0,y) x cos 90 = o =0 cos 0o = 1 r r = y tan 90o = y =~ tan 0o = 0 x 0o P(x,0) 90o r= x
- 13. Perbandingan Trigonometri dalam koordinat Cartesius r= (− 2) 2 + 32 = 13 (-2,3) 3 3 r sin α = 13 α -2 cos α = − 2 13 tan α = − 3 2
- 14. P(x,y) P(x,y) sin 2=y/r (+) sin 1=y/r (+) r cos 2=x/r (-) y r cos 1=x/r (+) tan 2=y/x (-) y tan 1=y/x (+) 2 1 x x 2 di kuadran II 1 di kuadran I P(x,y) x 3 4 x sin 3=y/r (-) sin 4=y/r (-) r cos 3=x/r (-) r cos 4=x/r (+) y y tan 4=y/x (-) tan 3=y/x (+) P(x,y) 3 di kuadran III 4 di kuadran IV
- 15. Tanda Perbandingan Trigonometri 90o sin, csc + Semua + II I 0o 180o III IV 360o tan,ctg + cos,sec + 270o
- 16. Contoh Soal 1. Diketahuitan =-5/12, sudut di kuadran IV, hitunglah : cot -12/5 cos 12/13 csc -13/5 2. Diketahui cos =1/3, hitunglah: a. sin b. tan KW I: 2√2/3 2√2 KW IV: -2√2/3 -2√2
- 17. Sudut-sudut Berelasi 90o sin (90o+α)=cos α sin (90o-α)=cos α cos(90o+α)=-sin α cos(90o-α)=sin α tan(90o+α)=-cot α tan(90o-α)=cot α sin (180o-α)=sin α sin (360o+α)=sinα cos(180o-α)=-cosα cos(360o+α)=cosα tan(180o-α)=-tan α II I 0o 180 o tan(360o+α)=tan α sin (180o+α)=-sin α sin (360o-α)=sin(- α)=-sinα III IV 360o cos(180o+α)=-cosα cos(360o-α)=cos(-α)=cosα tan(180o+α)=tan α tan(360o-α)=tan(- α )=-tan α sin (270o-α)=-cos α sin (270o+α)=-cos α cos(270o-α)=-sin α cos(270o+α)=sin α 270o tan(270 -α)=cot α o tan(270o+α)=-cot α
- 18.
- 19. Idetitas trigonometri Berdasarkan geometrianalitis: sin =y/r ⇒ y=r.sin cos =x/r ⇒ x=r.cos r2=x2+y2, maka: r2= (r.sin )2+(r.cos )2 r2= r2(sin 2 + cos 2 ) Sehingga : sin 2 + cos 2 =1
- 20. sin =y/r ⇒sin y/r y = = = tan cos =x/r cos x/r x sin cos = tan = cot cos sin sin =y/r ⇒ cos x/r = = cot cos =x/r sin y/r
- 21. sin 2 + cos 2 =1 Bagi kedua ruas dengan sin 2 : 1+cot2 =csc2 sin 2 + cos 2 =1 Bagi kedua ruas dengan cos 2 : tan2 +1=sec2
- 22. Contoh Penggunaan Rumus Identitas • Diketahui sin A=5/13 dan 90o<A<180o Tetukan nilai cos A & tan A! Jwb sin 2 A + cos 2 A =1⇒ cos 2 A =1- sin 2 A cos A=√ 1- sin 2 A, karena 90o<A<180o, maka cos A<0 ⇒ cos A=-√ 1- sin 2 A cos A=- √1-(5/13) 2= √144/169=-12/13 tanA=sinA/cosA=5/13:-12/13==-5/12
- 23. Rangkuman Identitas dasar: 1.sin 2 + cos 2 =1 2. : sin cos = tan = cot cos sin 3. 1+cot2 =csc2 4. tan2 +1=sec2
- 24. Cara Mudah menghafalsudut Istimewa • Grafik sinus
- 25.
- 26. • Grafik sindan cos
- 27.