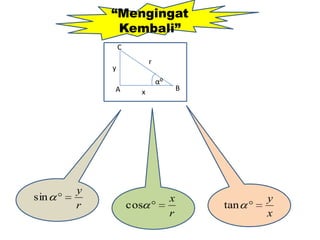
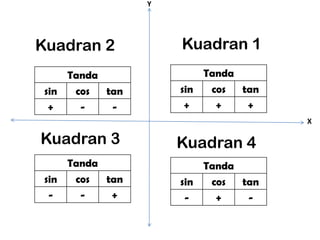
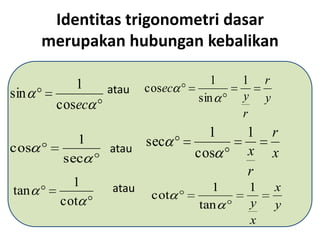
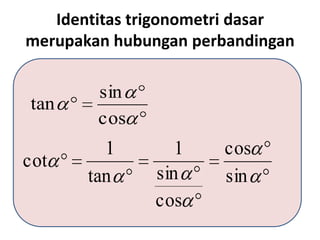
Dokumen ini membahas identitas trigonometri dasar, termasuk hubungan antara sinus, kosinus, dan tangen, serta aplikasinya dalam berbagai kuadran. Juga terdapat contoh soal yang menunjukkan penggunaan rumus untuk menghitung nilai trigonometri. Terakhir, ada pembuktian identitas trigonometri yang melibatkan sinus dan kosinus.