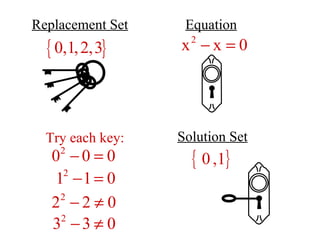
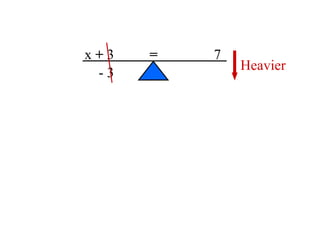
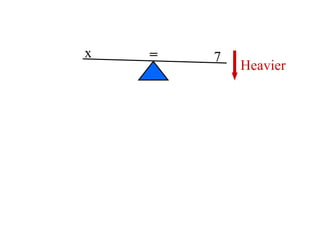
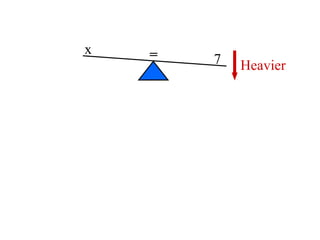
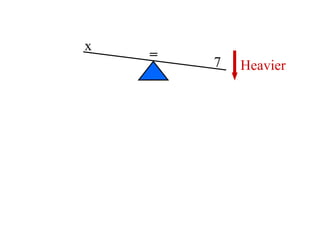
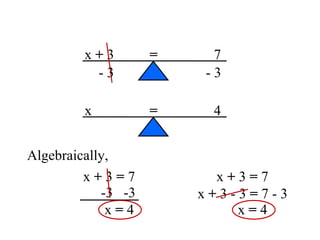
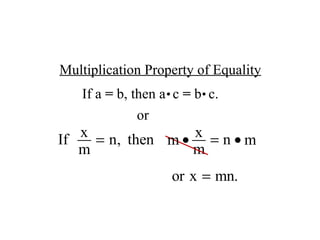The document discusses solving equations over replacement sets. It provides definitions of key terms like expressions, equations, inequalities, and open sentences. It then gives examples of identifying expressions, equations, inequalities, and whether sentences are true, false, or open. The document also covers properties of equality and strategies for solving equations, like isolating the variable.

1. Objective - To solve equations over given replacement sets. Equalities Inequalities = Equals- is the same as Congruent- same size and shape Similar- same shape < Is less than > Is greater than Is less than or equal to Approx. equal to = Not equal to ~

2. Expressions vs. Equations Numerical Variable Expressions Equations Inequalities 2 + 3 5(8) - 4 x + 7 8 - 3y 2 + 3 = 5 4 + 2(3) = 10 x - 4 = 13 11= 3 + 2m 9 - 5 > 3 6y - 4 < 8 Sentences Open sentences Open sentences have solutions and can be solved.

3. Identify each as an expression, sentence, open sentence, equation, or inequality. 1) 3x + 5 = 11 2) 7 < 2(5) + 3 3) 5x - 2 4) 6m + 2 > 3 Sentence, open sentence, equation Sentence, inequality Expression Sentence, open sentence, inequality

4. State whether each sentence is true, false , or open . 1) 8 + 5 = 13 2) 2x - 1 = 9 3) 17 = 3(5) + 1 4) 3 = 7(2) - 5 5) 14 - 2(3) = 8 6) 9 = 7 + 4y 7) 13 - 2 = 9 8) t + t = 5(2) + 1 True Open False False True Open False Open

5. Replacement Set Equation Solution Set Try each key:

6. Solve the given equation using the replacement set {0, 1, 2, 3, 4}. 1) 6 - x = 2 2) 2x + 1 = 5 3) 5x = 15 4) 11 = 4x + 3 5) 2x = x + x 6) 9 = 7 + 2y 7) x + 5 = 27 8) x + 2 = x {4} {2} {3} {2} {0, 1, 2, 3, 4} {1} { } , or “No solution” { } , or “No solution”

7. Addition Property of Equality If a = b, then a + c = b + c or Given a = b and c = c then a + c = b + c Subtraction Property of Equality If a = b, then a - c = b - c or Given a = b and c = c then a - c = b - c Equivalent Equations

8. = x + 3 7 - 3 Heavier

9. = x 7 Heavier

10. = x 7 Heavier

11. = x 7 Heavier

12. = x 7 Heavier

13. = x + 3 7 Algebraically, x + 3 = 7 -3 -3 x = 4 x + 3 = 7 x = 4 x + 3 - 3 = 7 - 3 - 3 - 3 = x 4

14. Rules for Transforming Equations 1) Goal: Isolate the variable on one side of the equation. 2) Always perform the same operation to both sides of an equation. 3) To undo an operation, perform its opposite operation to both sides of the equation.

15. Solve the equations below. The replacement set is the set of whole numbers. 1) x + 3 = 10 - 3 - 3 x = 7 2) y - 8 = 11 + 8 + 8 y = 19 3) n + 5 = 11 - 5 - 5 n = 6 4) 13 = x + 5 - 5 - 5 8 = x 5) 12 = n - 3 + 3 + 3 15 = n 6) 11 + 3 = k 14 = k

16. Translate the sentence into an equation and solve. 1) The sum of k and 13 is 28. 2) Five is the difference of t and 4. k + 13 = 28 - 13 - 13 k = 15 5 = t - 4 + 4 + 4 9 = t

17. Multiplication Property of Equality or If a = b, then a c = b c.

18. Solve given the replacement set is the set of whole numbers. 1) 2) 3) 4)

19. Division Property of Equality or

20. 1) 2) 3) 4) Solve given the replacement set is the set of whole numbers. No solution

21. Each pair of equations is equivalent. Tell what was done to the first equation to get the second. Four was subtracted from both sides. Nine was added to both sides. Each side was multiplied by 4.

22. Each pair of equations is equivalent. Tell what was done to the first equation to get the second. Each side was divided by 6. Six was subtracted from both sides. Each side was multiplied by 7.