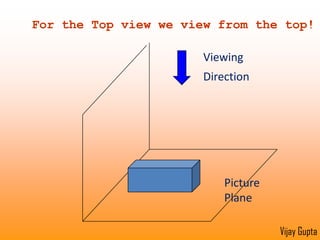
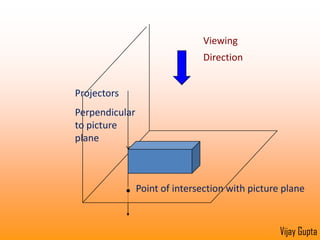
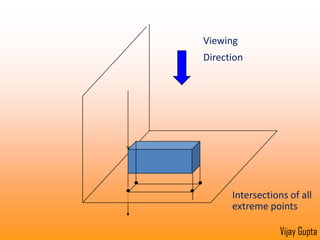
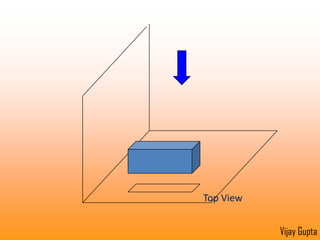
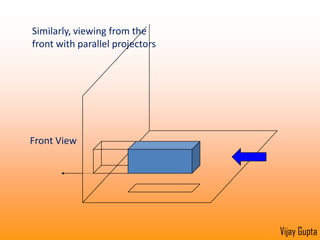
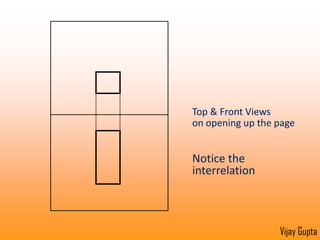
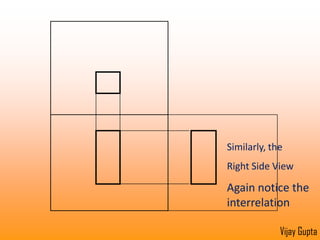
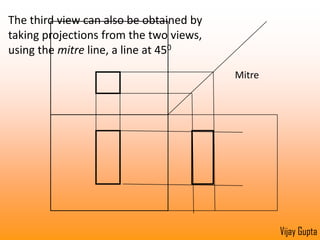
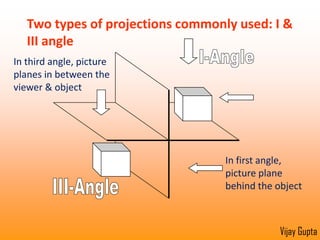
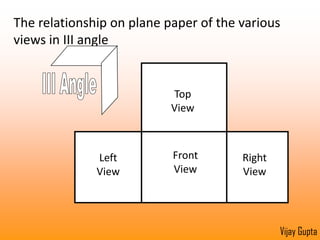
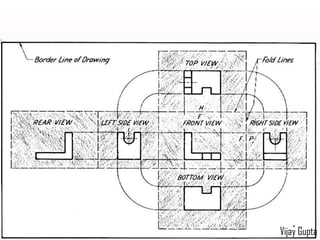
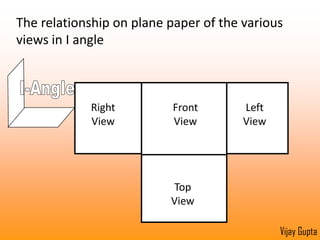
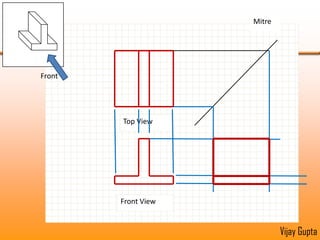
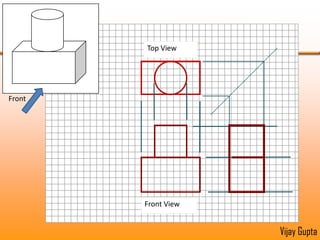
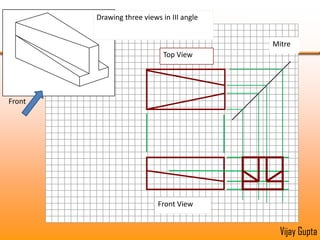
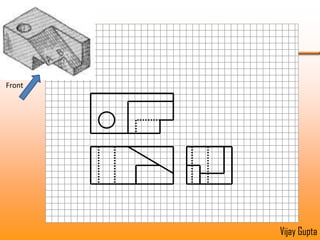
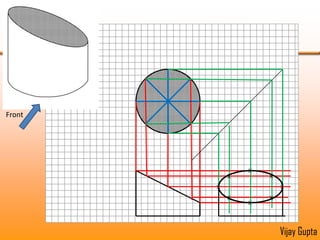
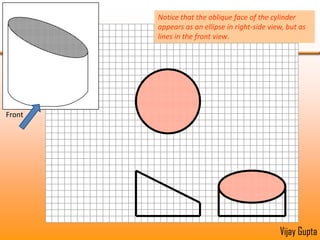
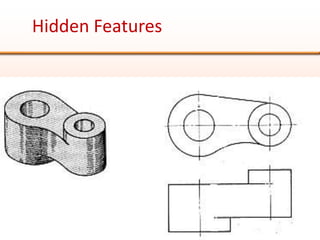
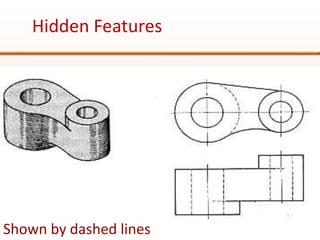
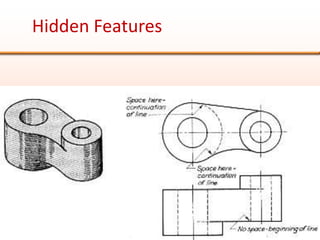
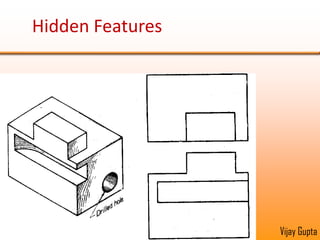
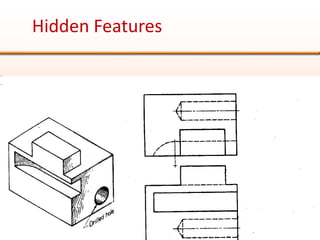
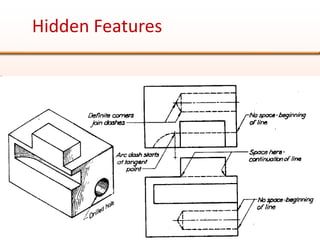
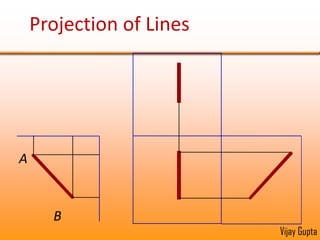
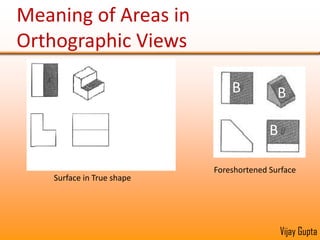
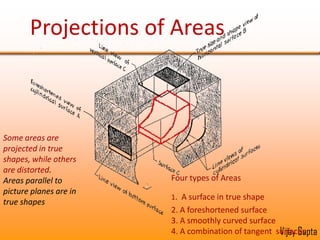
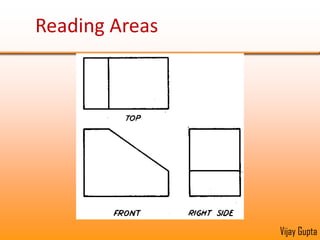
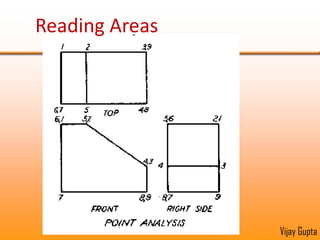
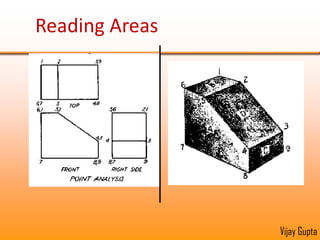
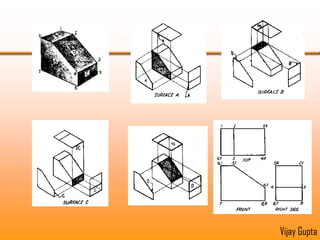
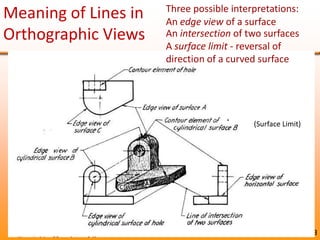
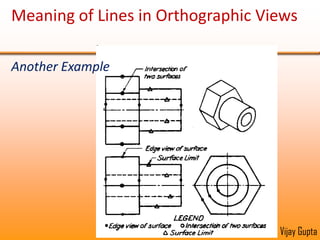
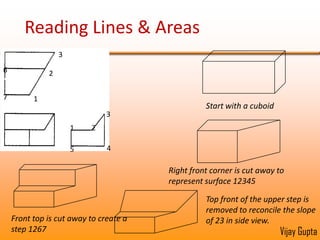
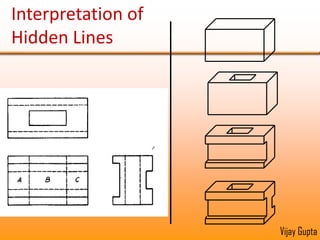
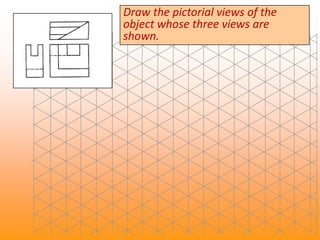
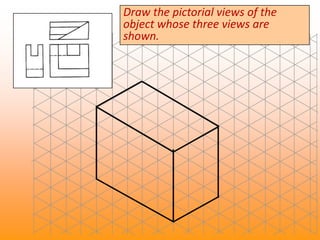
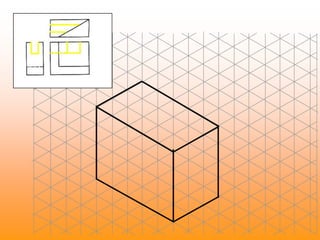
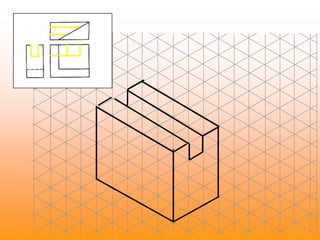
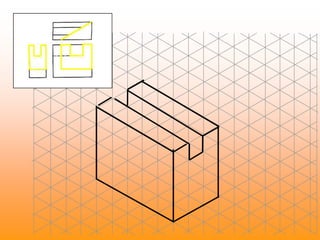
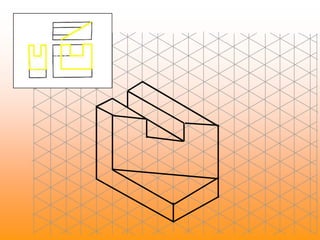
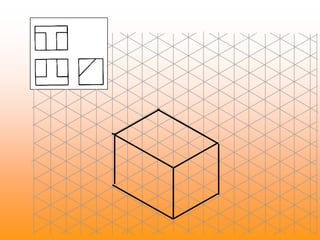
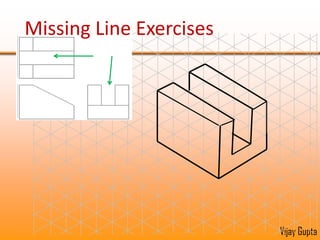
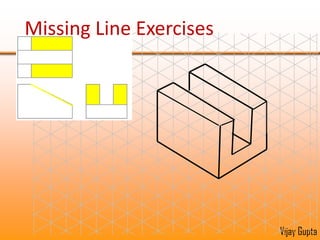
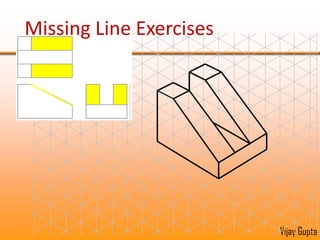
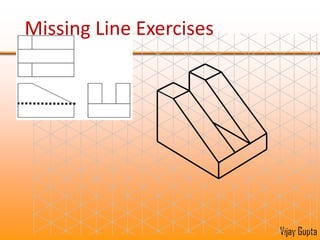
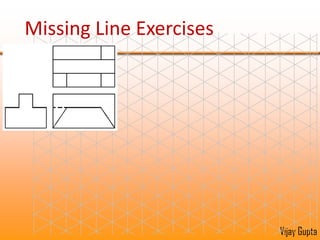
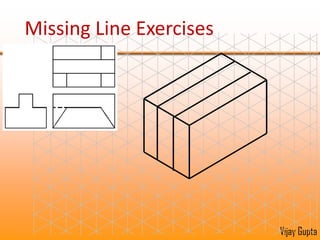
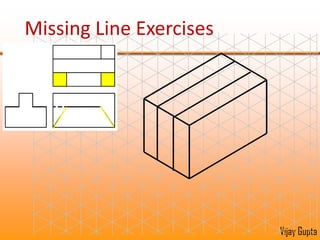
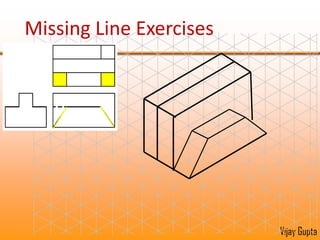
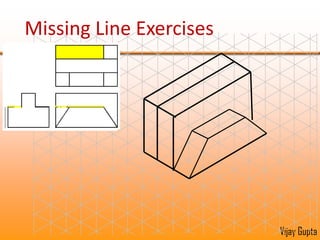
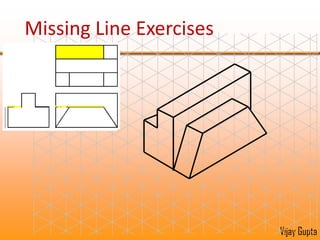
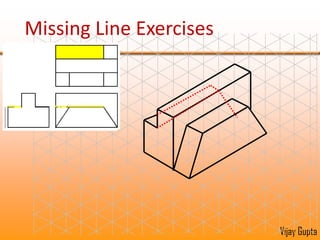
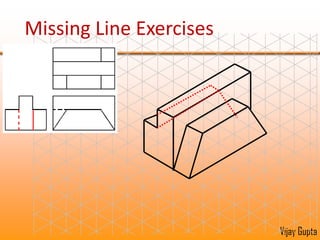
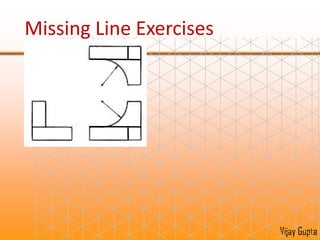
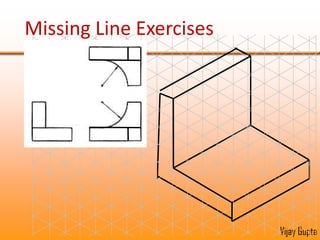
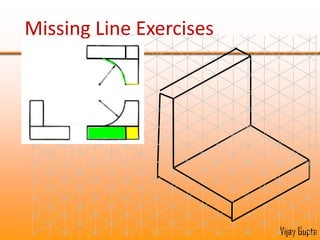
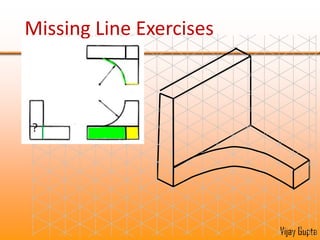
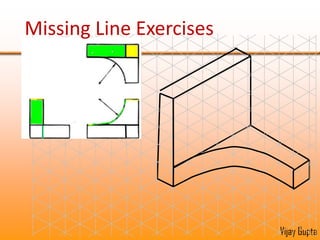
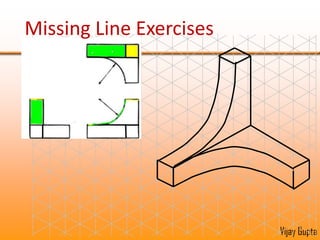
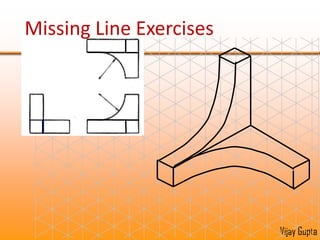
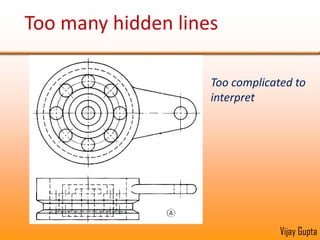
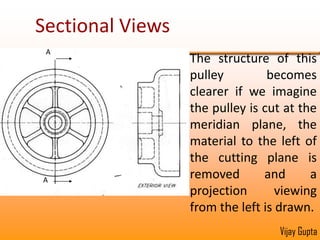
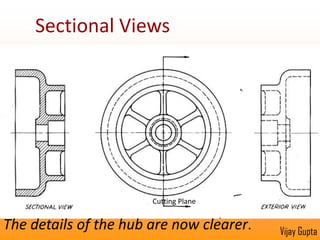
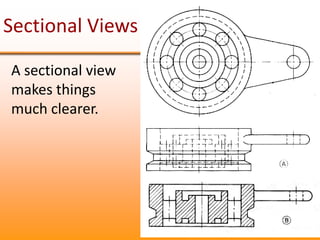
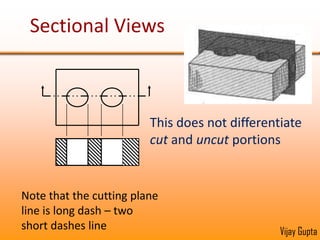
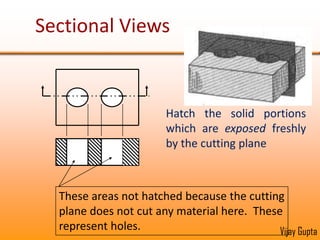
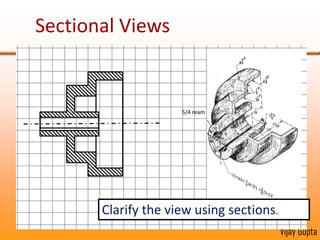
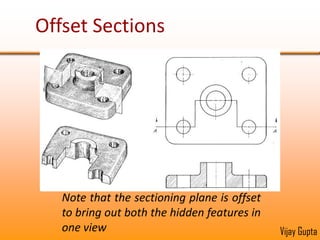
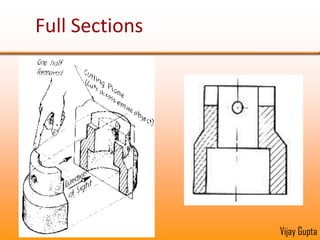
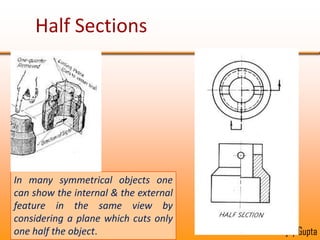
Orthographic projections are a method for conveying the shape and size of engineered objects using 2D drawings. They involve taking views of an object from the front, top, and side with parallel projecting rays. Lines and areas in the views represent edges, surfaces, and intersections between surfaces of the 3D object. Sectional views use a cutting plane to reveal internal features that would otherwise be hidden. They distinguish cut areas, which are hatched, from open areas cut through by the sectioning plane. Orthographic projections and sections effectively communicate 3D geometric information through 2D drawings.

1. Mechanical Sciences-I Chapter 7: Orthographic Projections

2. Introduction to Orthographic Projections Introducing Orthographic Projections as the language of engineering designers

4. An orthographic projection consists of the view obtained view when the object is viewed from very far away, so that the resulting rays are all parallel.

5. The parallel rays that are used for constructing the views are called projectors.Vijay Gupta

7. The intersections of the projectors with the picture plane are the projections of the points from which the projectors emanate.

8. The points are joined to obtain the views.Vijay Gupta

9. We consider here the development of the orthographic views of a simple object. Object Vijay Gupta

10. For the Top view we view from the top! Viewing Direction Picture Plane Vijay Gupta

11. Viewing Direction Projectors Perpendicular to picture plane Point of intersection with picture plane  Vijay Gupta

12. Viewing Direction     Intersections of all extreme points Vijay Gupta

13. Top View Vijay Gupta

14. Similarly, viewing from the front with parallel projectors Front View Vijay Gupta

15. Top & Front Views on opening up the page Notice the interrelation Vijay Gupta

16. Similarly, the Right Side View Again notice the interrelation Vijay Gupta

17. Mitre The third view can also be obtained by taking projections from the two views, using the mitre line, a line at 450 Vijay Gupta

18. Two types of projections commonly used: I & III angle I-Angle In third angle, picture planes in between the viewer & object In first angle, picture plane behind the object III-Angle Vijay Gupta

19. Opening up of the box with the various views in III angle Vijay Gupta

20. The relationship on plane paper of the various views in III angle III Angle Top View Front View Right View Left View Vijay Gupta

21. Vijay Gupta

22. I-Angle The relationship on plane paper of the various views in I angle Front View Left View Right View Top View Vijay Gupta

23. Vijay Gupta

24. Mitre Front Top View Front View Vijay Gupta

25. Top View Front Front View Vijay Gupta

26. Drawing three views in III angle Mitre Top View Front Front View Vijay Gupta

27. A Video Engg_graphics.mpg

28. A demonstration Vijay Gupta Gboxw31.exe

29. Front Vijay Gupta

30. Front X X X X X X X X Vijay Gupta

31. Notice that the oblique face of the cylinder appears as an ellipse in right-side view, but as lines in the front view. Front Vijay Gupta

32. Hidden Features

33. Hidden Features Shown by dashed lines

34. Hidden Features

35. Hidden Features

36. Hidden Features

37. Hidden Features

41. A line may be fore-shortened

43. Meaning of Areas in Orthographic Views B B B Foreshortened Surface Surface in True shape

44. Meaning of Areas in Orthographic Views C C D D C D Curved Surface Tangent Surfaces

45. Projections of Areas Some areas are projected in true shapes, while others are distorted. Areas parallel to picture planes are in true shapes Four types of Areas 1.A surface in true shape 2. A foreshortened surface 3. A smoothly curved surface 4. A combination of tangent surfaces

47. An plane surface that appears as a line in one view is normal to that view. It may or may not appear its true shape in the other views.

50. Reading Areas

51. Reading Areas

52. Reading Areas

54. Meaning of Lines in Orthographic Views Three possible interpretations: An edge view of a surface An intersection of two surfaces A surface limit - reversal of direction of a curved surface (Surface Limit)

56. An intersection of two surfaces

58. We next illustrate how to read the orthographic drawings. This is done by interpreting the three view to ‘draw’ the represented by those view.

59. Reading Lines & Areas Start with a cuboid 3 6 2 7 1 Right front corner is cut away to represent surface 12345 3 1 2 Top front of the upper step is removed to reconcile the slope of 23 in side view. 4 5 Front top is cut away to create a step 1267

60. Interpretation of Hidden Lines

61. Draw the pictorial views of the object whose three views are shown.

62. Draw the pictorial views of the object whose three views are shown.

77. Missing Line Exercises In the examples that follow, one or more lines may be missing in (only) one view. Try constructing a pictorial view to determine what line(s) are missing.

78. Missing Line Exercises One or more lines may be missing in (only) one view. Try constructing a pictorial view to determine what line(s) are missing.

79. Missing Line Exercises

80. Missing Line Exercises

81. Missing Line Exercises

82. Missing Line Exercises

83. Missing Line Exercises

84. Missing Line Exercises

85. Missing Line Exercises

86. Missing Line Exercises

87. Missing Line Exercises

88. Missing Line Exercises

89. Missing Line Exercises

90. Missing Line Exercises

91. Missing Line Exercises

92. Missing Line Exercises

93. Missing Line Exercises

94. Missing Line Exercises

95. Missing Line Exercises ?

96. Missing Line Exercises

97. Missing Line Exercises

98. Missing Line Exercises

99. Sectional Views

100. Sectional Views Whenever a representation becomes confused due to too many essential hidden details that it is difficult to interpret, sectional views are employed

101. Too many hidden lines Too complicated to interpret

103. For this purpose a cutting plane is employed. The shape of the object is clarified by distinguishing between the areas where the cutting plane actually cuts the solid material and the areas where it meets voids.

105. Sectional Views Cutting Plane The details of the hub are now clearer.

106. Sectional Views A sectional view makes things much clearer.

107. Sectional Views

108. Sectional Views This does not differentiate cut and uncut portions Note that the cutting plane line is long dash – two short dashes line

109. Sectional Views Hatch the solid portions which are exposed freshly by the cutting plane These areas not hatched because the cutting plane does not cut any material here. These represent holes.

110. Sectional Views 5/4 ream Clarify the view using sections.

113. Full Sections

114. Half Sections In many symmetrical objects one can show the internal & the external feature in the same view by considering a plane which cuts only one half the object.