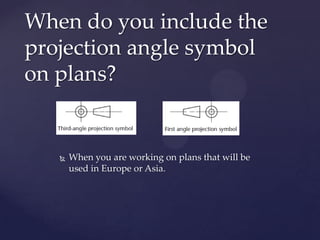
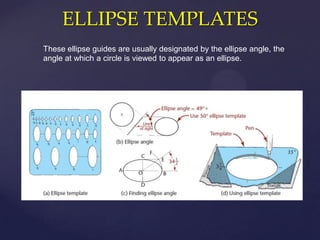
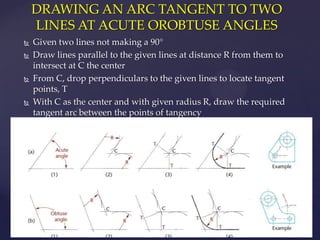
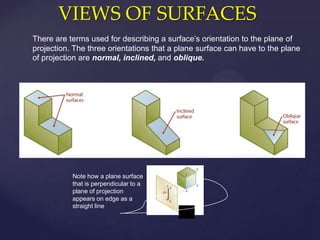
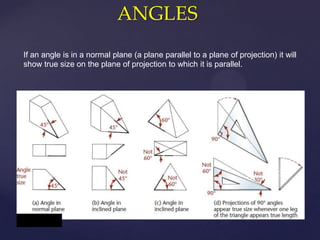
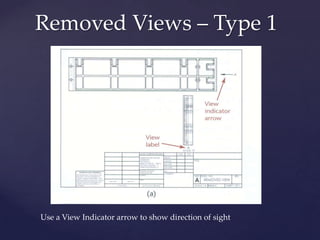
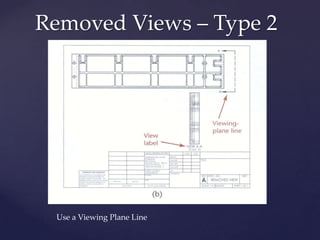
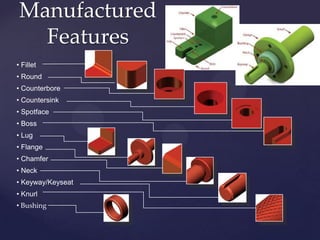
This document provides information about a 2D Essentials class taught by Laura Gerold. The class includes four sections with start and end dates of January 18, 2012 to May 16, 2012. The document then provides questions from students and answers from the instructor on topics that will be covered in the class, including when to include projection angles, how to draw ellipses using foci, drawing arcs tangent to lines, and a test review with potential topics.
This temple is a tribute and a reflection of the power of its patron, Raja Raja Chola I. An integral part of ancient Indian architecture's greatest glories, it is today a UNESCO World Heritage Site as “Great Living Chola Temples”. Know More : https://www.ishtadevata.com/brihadeeswarar-temple-thanjavur.html
Chapter- 17 Forests - Our Lifeline Class 7th ppt. This Chapter is taken from NCERT Class 7th Science textbook. This ppt is only for Class 7th students.
Topics Included:
• Origin
• Definition and Example
• Type of Magnets
• Type of Materials
• Properties of Magnet
• Methods to make a Magnet
• Magnetic Compass
• Difference between Permanent and Temporary Magnet
• Important Definitions
• Worksheet
This temple is a tribute and a reflection of the power of its patron, Raja Raja Chola I. An integral part of ancient Indian architecture's greatest glories, it is today a UNESCO World Heritage Site as “Great Living Chola Temples”. Know More : https://www.ishtadevata.com/brihadeeswarar-temple-thanjavur.html
Chapter- 17 Forests - Our Lifeline Class 7th ppt. This Chapter is taken from NCERT Class 7th Science textbook. This ppt is only for Class 7th students.
Topics Included:
• Origin
• Definition and Example
• Type of Magnets
• Type of Materials
• Properties of Magnet
• Methods to make a Magnet
• Magnetic Compass
• Difference between Permanent and Temporary Magnet
• Important Definitions
• Worksheet
Chapter 10 of Science of class 1th, Very nice animated and the best powerpoint for the children, it made by me; Abhishek Bhartee, not downloaded from any other website.
It is Awesome
Click Here: https://www.digistore24.com/redir/269221/Manikji/
Topics Included:
• Inside View of a Torch
• Electric Bulb
• Filament
• Terminal
• Electrical Energy
• Electric Cell
• Electric Circuit
• Types of Circuit
• Open and Closed Switch
• Solar Cell
• Conductor and Insulator
• Different Methods of Producing Electricity
This PPT is based on Physics on Chapter Motion. In this you will find every thing of that chapter with great images. in this PPT their are many animation and images .
thank you
Food is the basic need for the all living organism. So, food is essential for all living organisms.
Food gives us energy to do work, growth and development of the body, and also to maintain good health by the functions of the body organs.
To make our food tasty, we use different ingredients for different varieties of food we eat.
A power point that is designed to explain the effects of the Rotation and Revolution on the Earth.
-Day and Night
-The four seasons
-Solstice and Equinox
-High tide and low tide
-Windspeed and Direction
it is attractive and it is for your education. I have used many attractive animations and it has good amount of study material.
The aim of this ppt is to give you more information about pollution, images are also added to make it more attractive
Chapter 10 of Science of class 1th, Very nice animated and the best powerpoint for the children, it made by me; Abhishek Bhartee, not downloaded from any other website.
It is Awesome
Click Here: https://www.digistore24.com/redir/269221/Manikji/
Topics Included:
• Inside View of a Torch
• Electric Bulb
• Filament
• Terminal
• Electrical Energy
• Electric Cell
• Electric Circuit
• Types of Circuit
• Open and Closed Switch
• Solar Cell
• Conductor and Insulator
• Different Methods of Producing Electricity
This PPT is based on Physics on Chapter Motion. In this you will find every thing of that chapter with great images. in this PPT their are many animation and images .
thank you
Food is the basic need for the all living organism. So, food is essential for all living organisms.
Food gives us energy to do work, growth and development of the body, and also to maintain good health by the functions of the body organs.
To make our food tasty, we use different ingredients for different varieties of food we eat.
A power point that is designed to explain the effects of the Rotation and Revolution on the Earth.
-Day and Night
-The four seasons
-Solstice and Equinox
-High tide and low tide
-Windspeed and Direction
it is attractive and it is for your education. I have used many attractive animations and it has good amount of study material.
The aim of this ppt is to give you more information about pollution, images are also added to make it more attractive
Mathematics Quiz on Area and Perimeter for Class 7LAL CHAND GOYAL
Power point presentation made by Arnav Goyal, class-7 student, Amity International School, Sector-43,Gurgaon, for the benefit of the students who want to learn area and perimeter for competitive exams.
Mathematics Quiz on Area on Perimeter for class 7LAL CHAND GOYAL
PPT. prepared by me, student of class 7, Amity International School, Sector - 43, Gurgaon for the benefit of those students who want to learn Area and Perimeter for competitive exams.
Social Media Platforms, Insights & Data - Engage Bali 2016 by Jan RezabJan Rezab
Presentation from Engage Bali, where we spoke about some amazing data trends, social video, social insights, talking about what is necessary in terms of subtitles on videos, etc.
Acetabularia Information For Class 9 .docxvaibhavrinwa19
Acetabularia acetabulum is a single-celled green alga that in its vegetative state is morphologically differentiated into a basal rhizoid and an axially elongated stalk, which bears whorls of branching hairs. The single diploid nucleus resides in the rhizoid.
The French Revolution, which began in 1789, was a period of radical social and political upheaval in France. It marked the decline of absolute monarchies, the rise of secular and democratic republics, and the eventual rise of Napoleon Bonaparte. This revolutionary period is crucial in understanding the transition from feudalism to modernity in Europe.
For more information, visit-www.vavaclasses.com
June 3, 2024 Anti-Semitism Letter Sent to MIT President Kornbluth and MIT Cor...Levi Shapiro
Letter from the Congress of the United States regarding Anti-Semitism sent June 3rd to MIT President Sally Kornbluth, MIT Corp Chair, Mark Gorenberg
Dear Dr. Kornbluth and Mr. Gorenberg,
The US House of Representatives is deeply concerned by ongoing and pervasive acts of antisemitic
harassment and intimidation at the Massachusetts Institute of Technology (MIT). Failing to act decisively to ensure a safe learning environment for all students would be a grave dereliction of your responsibilities as President of MIT and Chair of the MIT Corporation.
This Congress will not stand idly by and allow an environment hostile to Jewish students to persist. The House believes that your institution is in violation of Title VI of the Civil Rights Act, and the inability or
unwillingness to rectify this violation through action requires accountability.
Postsecondary education is a unique opportunity for students to learn and have their ideas and beliefs challenged. However, universities receiving hundreds of millions of federal funds annually have denied
students that opportunity and have been hijacked to become venues for the promotion of terrorism, antisemitic harassment and intimidation, unlawful encampments, and in some cases, assaults and riots.
The House of Representatives will not countenance the use of federal funds to indoctrinate students into hateful, antisemitic, anti-American supporters of terrorism. Investigations into campus antisemitism by the Committee on Education and the Workforce and the Committee on Ways and Means have been expanded into a Congress-wide probe across all relevant jurisdictions to address this national crisis. The undersigned Committees will conduct oversight into the use of federal funds at MIT and its learning environment under authorities granted to each Committee.
• The Committee on Education and the Workforce has been investigating your institution since December 7, 2023. The Committee has broad jurisdiction over postsecondary education, including its compliance with Title VI of the Civil Rights Act, campus safety concerns over disruptions to the learning environment, and the awarding of federal student aid under the Higher Education Act.
• The Committee on Oversight and Accountability is investigating the sources of funding and other support flowing to groups espousing pro-Hamas propaganda and engaged in antisemitic harassment and intimidation of students. The Committee on Oversight and Accountability is the principal oversight committee of the US House of Representatives and has broad authority to investigate “any matter” at “any time” under House Rule X.
• The Committee on Ways and Means has been investigating several universities since November 15, 2023, when the Committee held a hearing entitled From Ivory Towers to Dark Corners: Investigating the Nexus Between Antisemitism, Tax-Exempt Universities, and Terror Financing. The Committee followed the hearing with letters to those institutions on January 10, 202
Macroeconomics- Movie Location
This will be used as part of your Personal Professional Portfolio once graded.
Objective:
Prepare a presentation or a paper using research, basic comparative analysis, data organization and application of economic information. You will make an informed assessment of an economic climate outside of the United States to accomplish an entertainment industry objective.
Francesca Gottschalk - How can education support child empowerment.pptxEduSkills OECD
Francesca Gottschalk from the OECD’s Centre for Educational Research and Innovation presents at the Ask an Expert Webinar: How can education support child empowerment?
Read| The latest issue of The Challenger is here! We are thrilled to announce that our school paper has qualified for the NATIONAL SCHOOLS PRESS CONFERENCE (NSPC) 2024. Thank you for your unwavering support and trust. Dive into the stories that made us stand out!
Model Attribute Check Company Auto PropertyCeline George
In Odoo, the multi-company feature allows you to manage multiple companies within a single Odoo database instance. Each company can have its own configurations while still sharing common resources such as products, customers, and suppliers.
How to Make a Field invisible in Odoo 17Celine George
It is possible to hide or invisible some fields in odoo. Commonly using “invisible” attribute in the field definition to invisible the fields. This slide will show how to make a field invisible in odoo 17.
1. 2D Essentials
Instructor: Laura Gerold, PE
Catalog #10614113
{ Class # 22784, 24113, 24136, & 24138
Class Start: January 18, 2012 Class End:
May 16, 2012
3. When do you include the
projection angle symbol
on plans?
When you are working on plans that will be
used in Europe or Asia.
4. ELLIPSE TEMPLATES
These ellipse guides are usually designated by the ellipse angle, the
angle at which a circle is viewed to appear as an ellipse.
5. DRAWING A FOCI ELLIPSE
Major axis = long axis of ellipse
Minor axis = short axis of ellipse
The foci of the ellipse are two special points E and F on
the ellipse's major axis and are equidistant from the
center point. The sum of the distances from any point P
on the ellipse to those two foci is constant and equal to
the major axis ( PE + PF2= 2A ). Each of these two points
is called a focus of the ellipse.
6. DRAWING A FOCI ELLIPSE
Let AB be the major axis and CD the minor axis
To find foci E and F, draw arcs R with radius equal to half the major
axis and centers at the end of the minor axis
Between E and O on the major axis, mark at random a number of
points.
Using a random point (point 3), with E and F as centers and radii A-3
and B-3, draw arcs to intersect at four points 3’. Use the remaining
points to find four additional points on the ellipse in the same
manner.
Sketch the ellipse lightly through the points
7. Drawing an Ellipse
Draw a major axis 5” long and a minor axis 2.5” long.
Draw an ellipse by the foci method with at least five
points in each quadrant
8. DRAWING AN ARC TANGENT TO TWO
LINES AT ACUTE OROBTUSE ANGLES
Given two lines not making a 90°
Draw lines parallel to the given lines at distance R from them to
intersect at C the center
From C, drop perpendiculars to the given lines to locate tangent
points, T
With C as the center and with given radius R, draw the required
tangent arc between the points of tangency
9. DRAWING AN ARC TANGENT TO TWO
LINES AT ACUTE OROBTUSE ANGLES
Draw two intersecting lines at an acute
angle, each 2.5 inches long
Draw a 1.5 inch radius arc tangent to the
two lines
11. How Many Questions are
on the Test?
50
You have the entire class
period to complete the test
12. How are the questions
formatted?
True and False
Multiple Choice
Fill in the Blank
Essay Questions
Drawing
13. What can I bring?
All of your drawing utensils
A Calculator
This is NOT an open book exam.
Other electronic devices can not be used
in place of a calculator
14. What do I need to know
how to draw?
Circles
Squares
Bisect an angle
Perpendicular Bisect a line
Triangles
Orthographic Sketches
Alphabet of Lines
Lettering
15. What Chapters in the
Book Will be Covered?
Chapter 1
Chapter 2
Chapter 3 (Sections 1-5)
Chapter 4
Chapter 5
16. What Should I Use to
Study?
Class Notes (Power Points on Blackboard)
Class Notes you took
Homework
Textbook
17. Potential Topics on Test
Identify and Describe the five phases of the design
process
Identify what technical drawings are used for
Identify why drawing by hand is still useful
Identify who creates technical drawings and what
professions use them
Draw & Identify the Alphabet of Lines
18. Potential Topics on Test
Apply civil engineering scales to sketches of simple
objects
Apply architectural scales to sketches of simple
objects
Scale a drawing up or down using scale ratios (ex
1:2, 2:1)
Apply standard lettering practice and standards to
sketches
Identify negative space
19. Potential Topics on Test
Describe Prisms
Describe Cylinders
Describe Pyramids
Describe Cones
Describe Spheres
Describe a Torus
Describe Ellipsoids
20. Potential Topics on Test
Describe Parallelograms
Describe a Trapezoid
Describe a Trapezium
Describe a Regular Polygon up to 8 Sides
Describe a Circumference of a Circle
Describe Diameter of a Circle
Describe Radius of a Circle
Describe a Quadrant of a Circle
Describe a Chord of a Circle
Describe Concentric Circles
Describe Eccentric Circles
Identify the point at which a line is tangent to an arc
Identify the pint at which an arc is tangent to an arc
21. Potential Topics on Test
Differentiate between the 1st and 3rd Angle
Projection
Name and position the 6 primary views
Create orthographic sketches of simple objects
Transfer dimensions
Apply hidden line conventions to sketches
Apply line precedence conventions to sketches
22. What are you confused
about?
Write down a question that you still have about a
topic that will be covered on the test.
Share the question and topic with your group
As a group determine the answer to the question
Still stumped? Ask a neighboring group
Classroom stumped? Save the question for the end
and ask me
23. Stand up and Stretch . . .
It’s time for a review
game!
24. Information Domination
Which Team Will Dominate? Winning team will each receive 5
extra credit points.
Pick a team name
Team members pick a category and answer the next question in
that category
All question are answered in order starting with 1 then 2, etc.
If the team answers correctly, they get 2 points
If they have to use their text to answer, they only get 1 point
If nobody on the team is able to answer the question correctly,
they can say “pass.” The next team gets a chance to answer for 1
point.
28. VIEWS OF SURFACES
There are terms used for describing a surface’s orientation to the plane of
projection. The three orientations that a plane surface can have to the plane
of projection are normal, inclined, and oblique.
Note how a plane surface
that is perpendicular to a
plane of projection
appears on edge as a
straight line
30. Normal Surfaces
A normal surface is parallel to the plane of
projection
It appears its true shape and size on orthographic
drawings.
A edges are true length on plane of projection
31. “Normal” Group Project
Use your blocks to make a creation
different than last week
Sketch the three necessary views
33. Inclined Surfaces
An inclined surface is perpendicular to one plane of
projection
It is inclined or tipped to adjacent planes
Inclined edge is parallel to one plane of projection and
appears true length on this plan (appears as angled line)
Inclined edge appears as a foreshortened line on adjacent
planes (appears as horizontal or vertical line)
34. “Inclined” Group Project
Each group gets a right triangular prism
Draw the three necessary views
What was different about drawing the inclined planes
versus the normal planes (with the blocks)?
36. Oblique Surfaces
An oblique surface is tipped on all principal planes of
projections
It does not appear on edge or true size in any standard
view
An oblique edge appears foreshortened and at an angle in
every view
37. “Oblique” Group Project
As a group, try to think of any oblique surfaces
you have seen at home, work, or on your way
here tonight.
Sketch up a few and present to class
38. ANGLES
If an angle is in a normal plane (a plane parallel to a plane of projection) it will
show true size on the plane of projection to which it is parallel.
44. Group Project – Removed
Views
Remove a View from one of your group
drawings of today
Create a removed view plane using an
indicator arrow or viewing plane line
48. What’s Next?
• Test next week – March 7th
• Spring Break March 14th - NO CLASS
• Finish Chapter 6 – 2D Drawing Representation
on March 21st
49. On one of your sketches, answer the
following two questions:
What was the most useful thing that you
learned today?
What do you still have questions about?
Questions?
50. Chapter 5 Review Question: 5
Chapter 5 Exercises: 5.2, 5.5 (9), 5.6 (8– no
isometric drawing)
Homework – Due March
21st!
