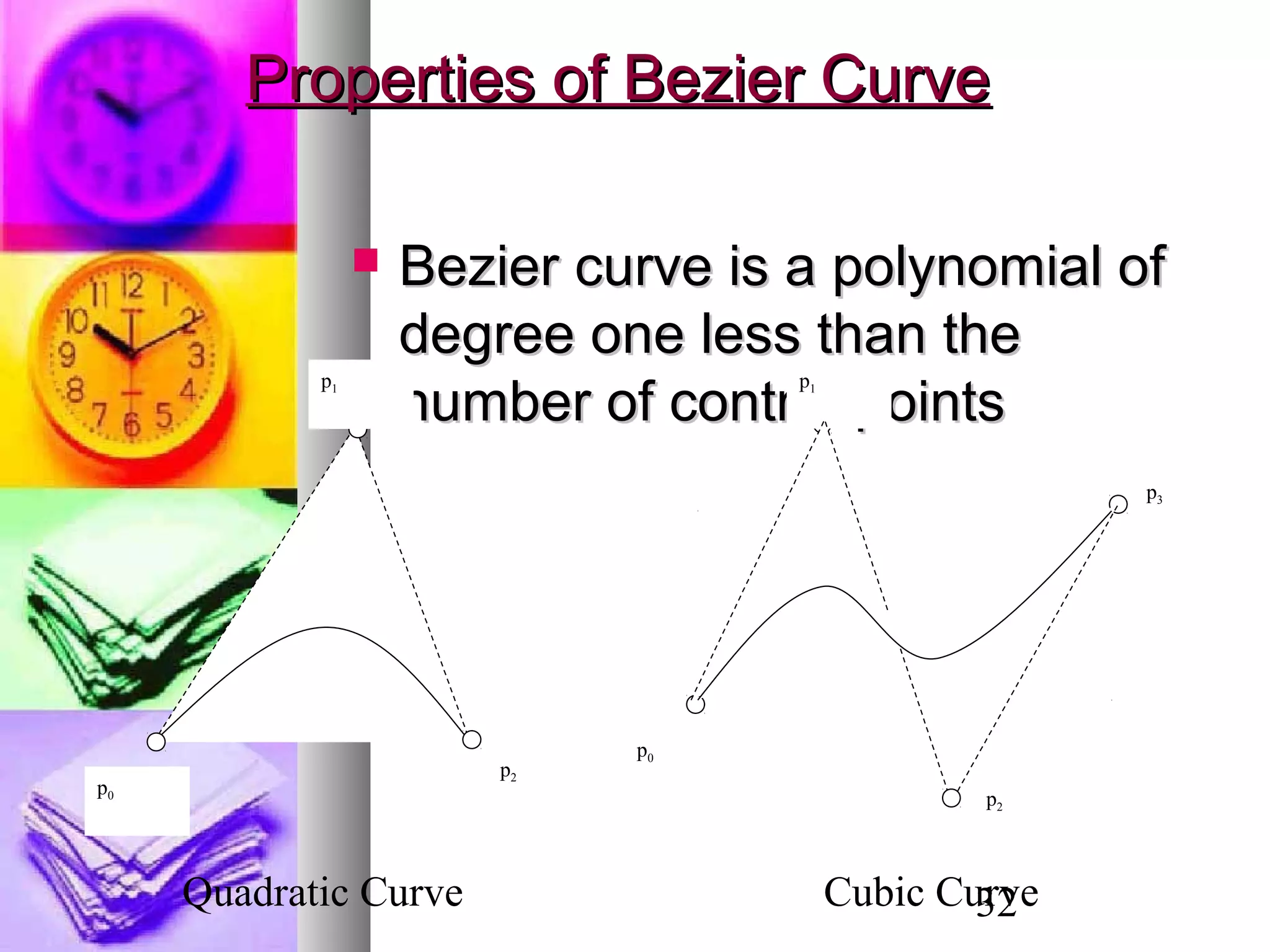
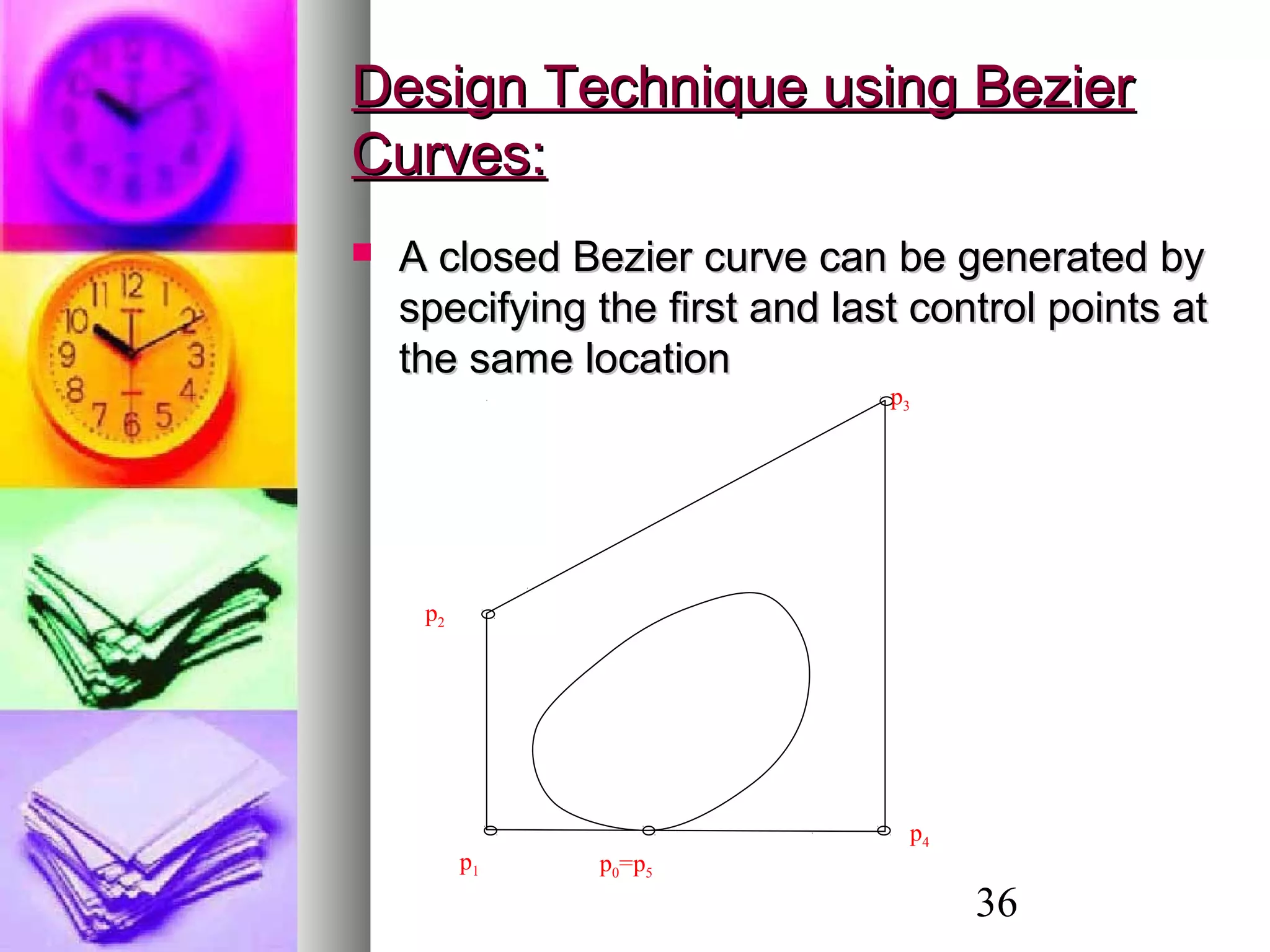
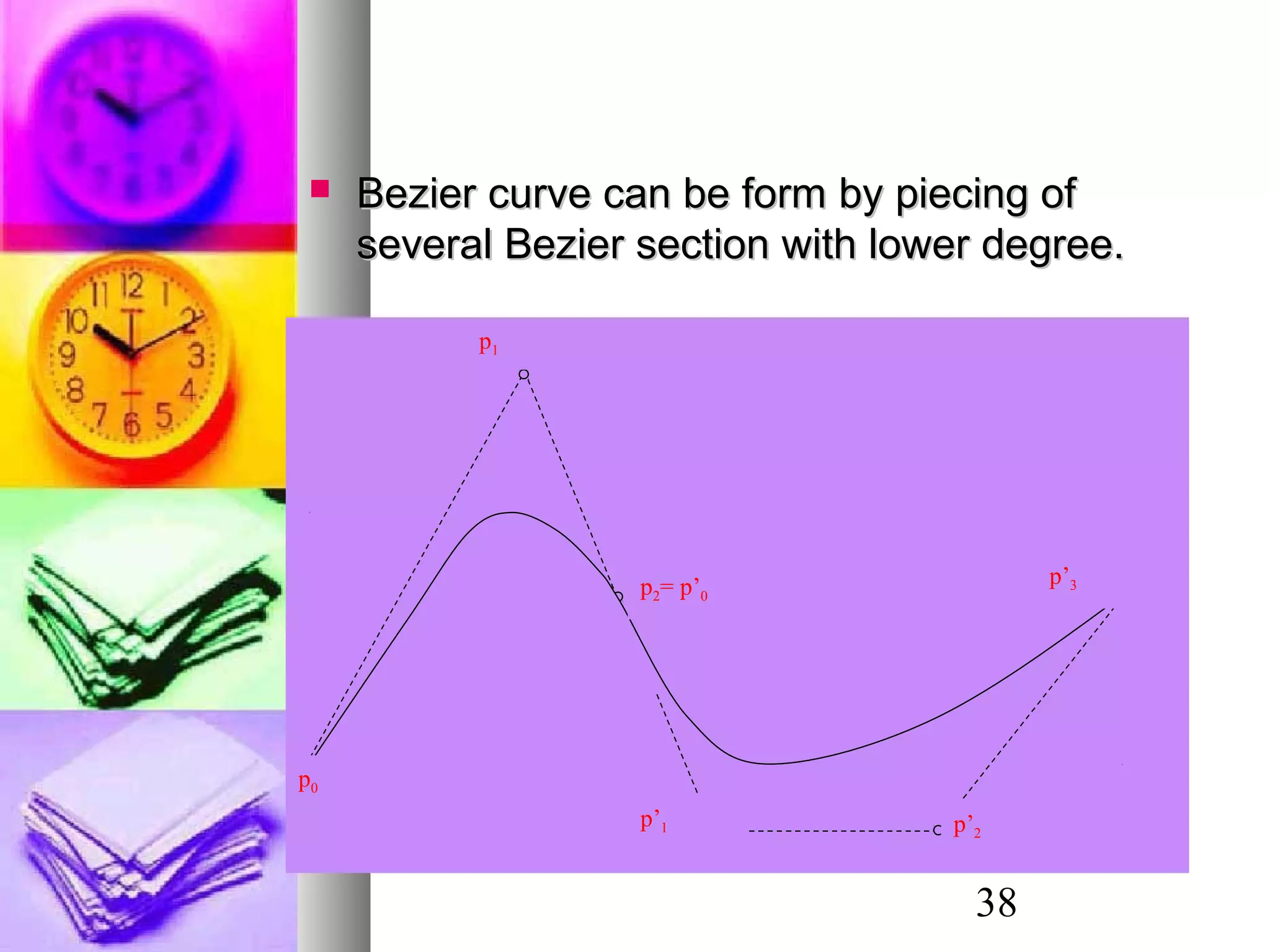
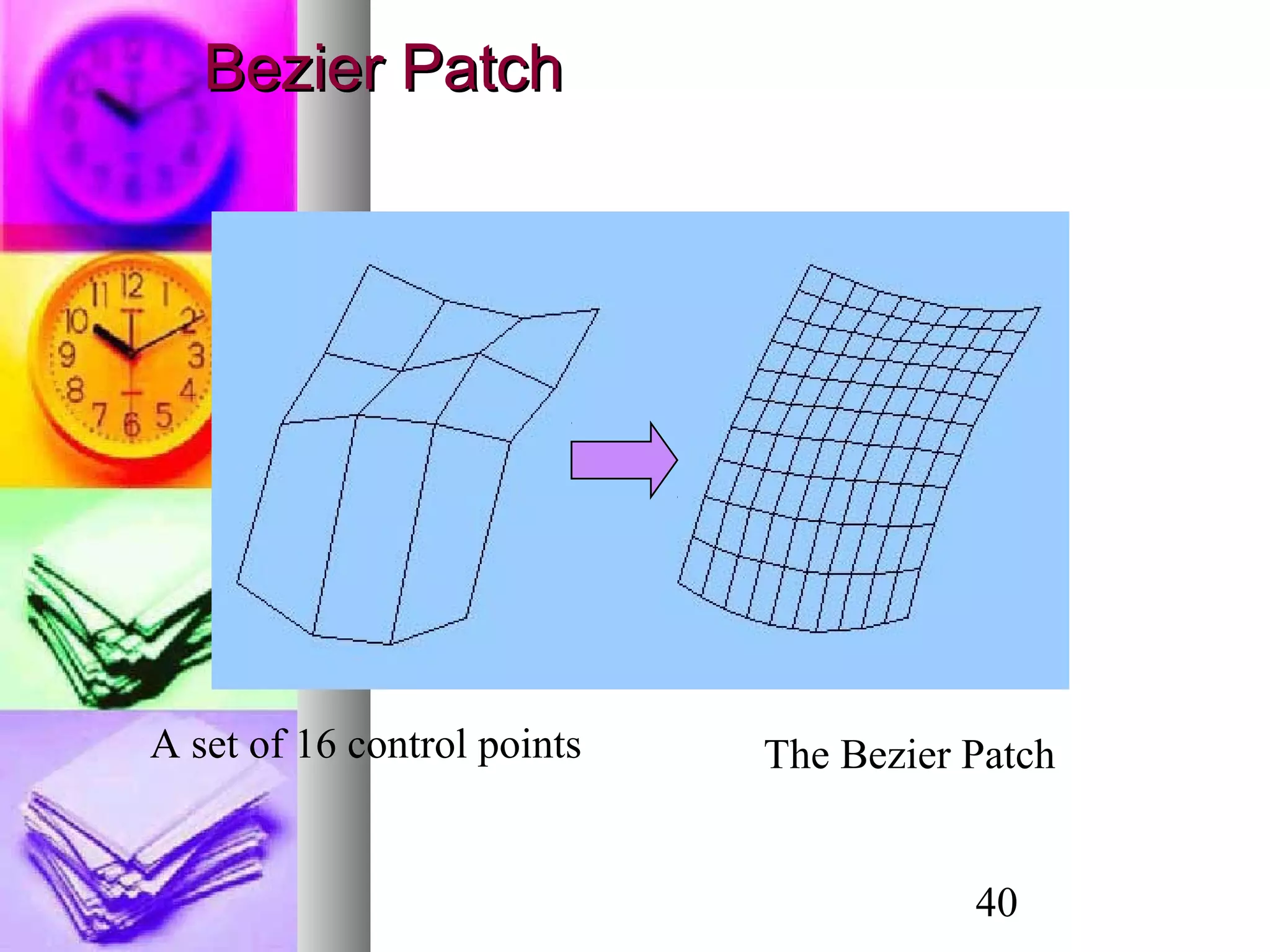
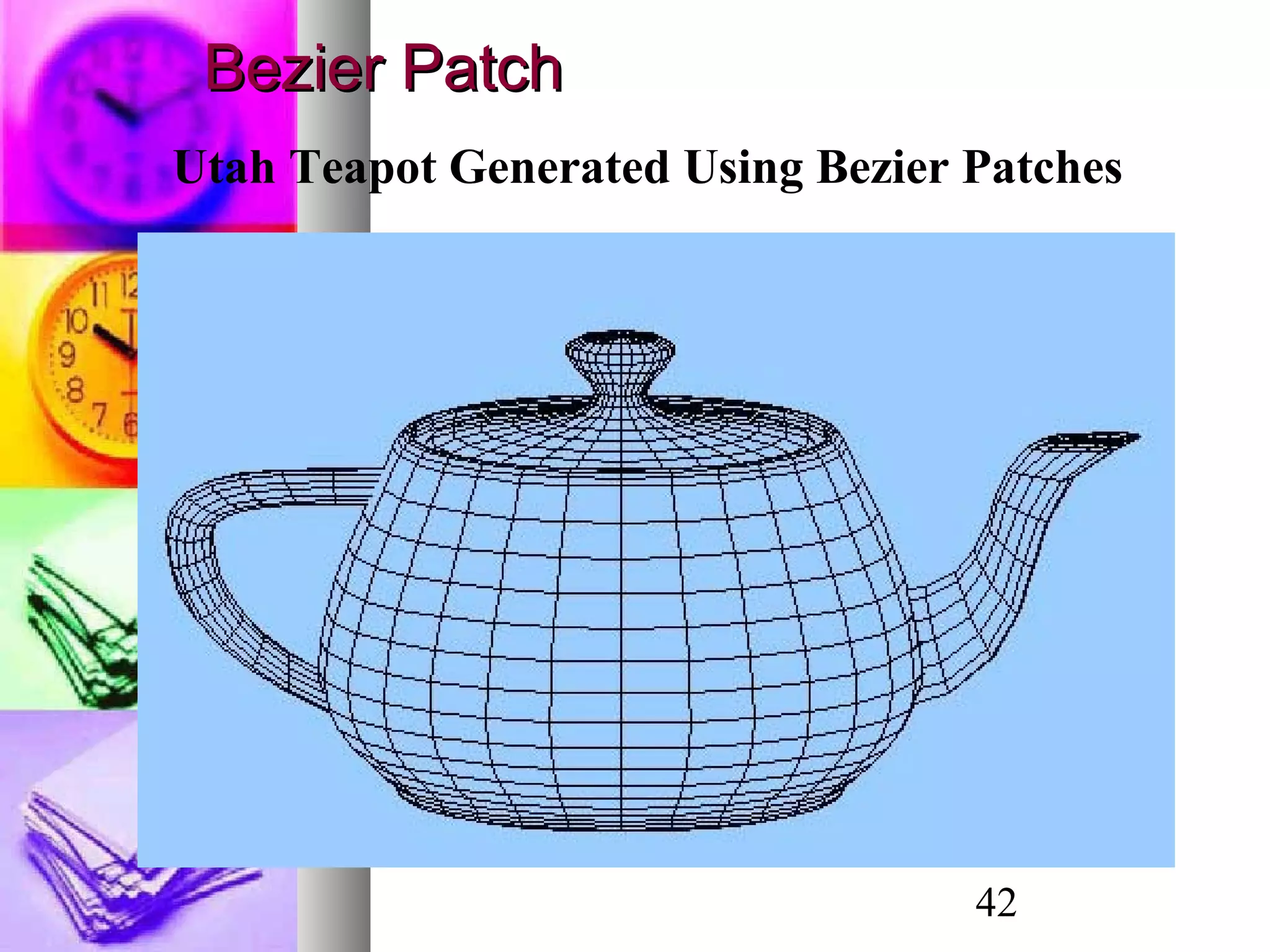
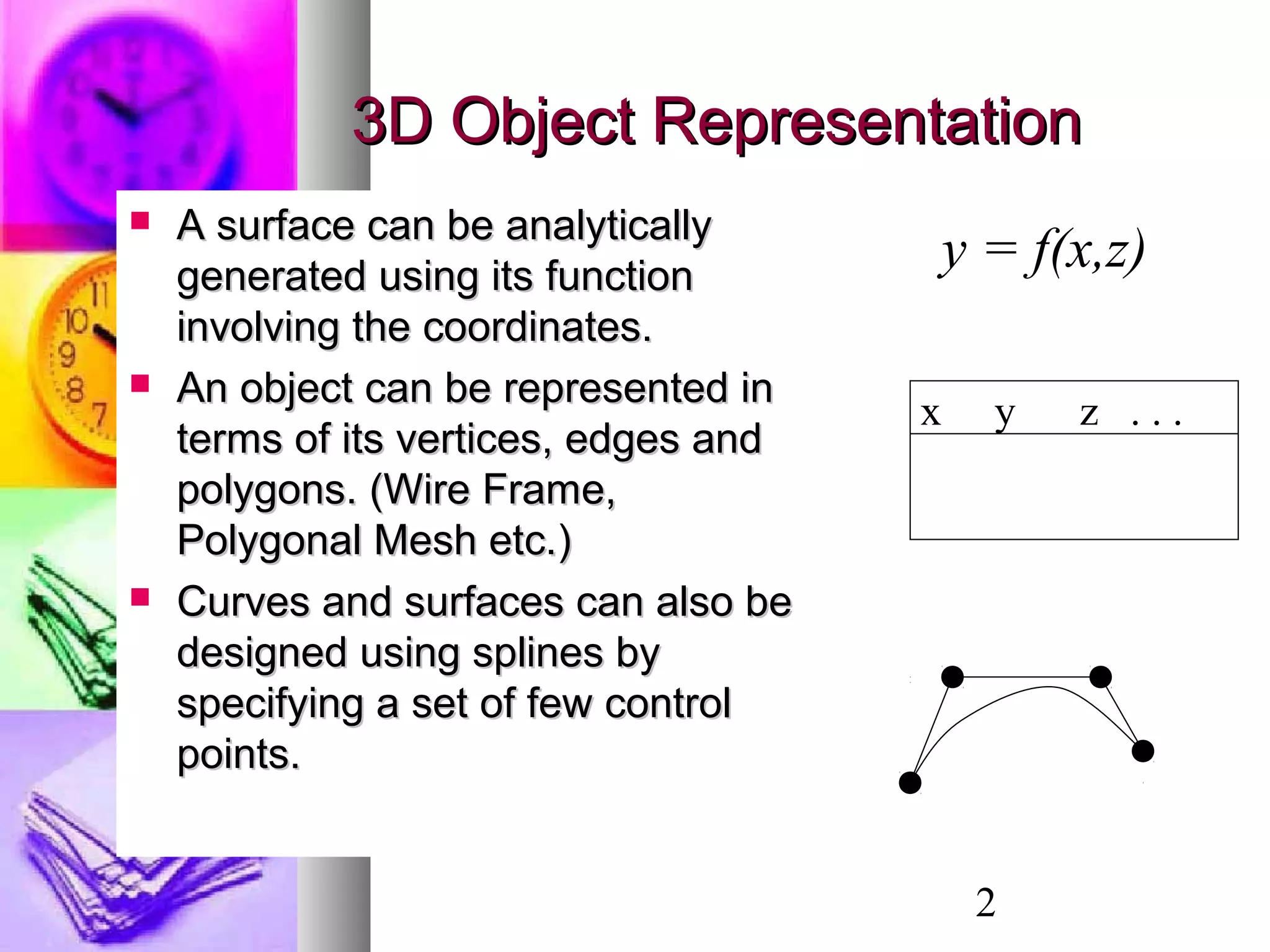
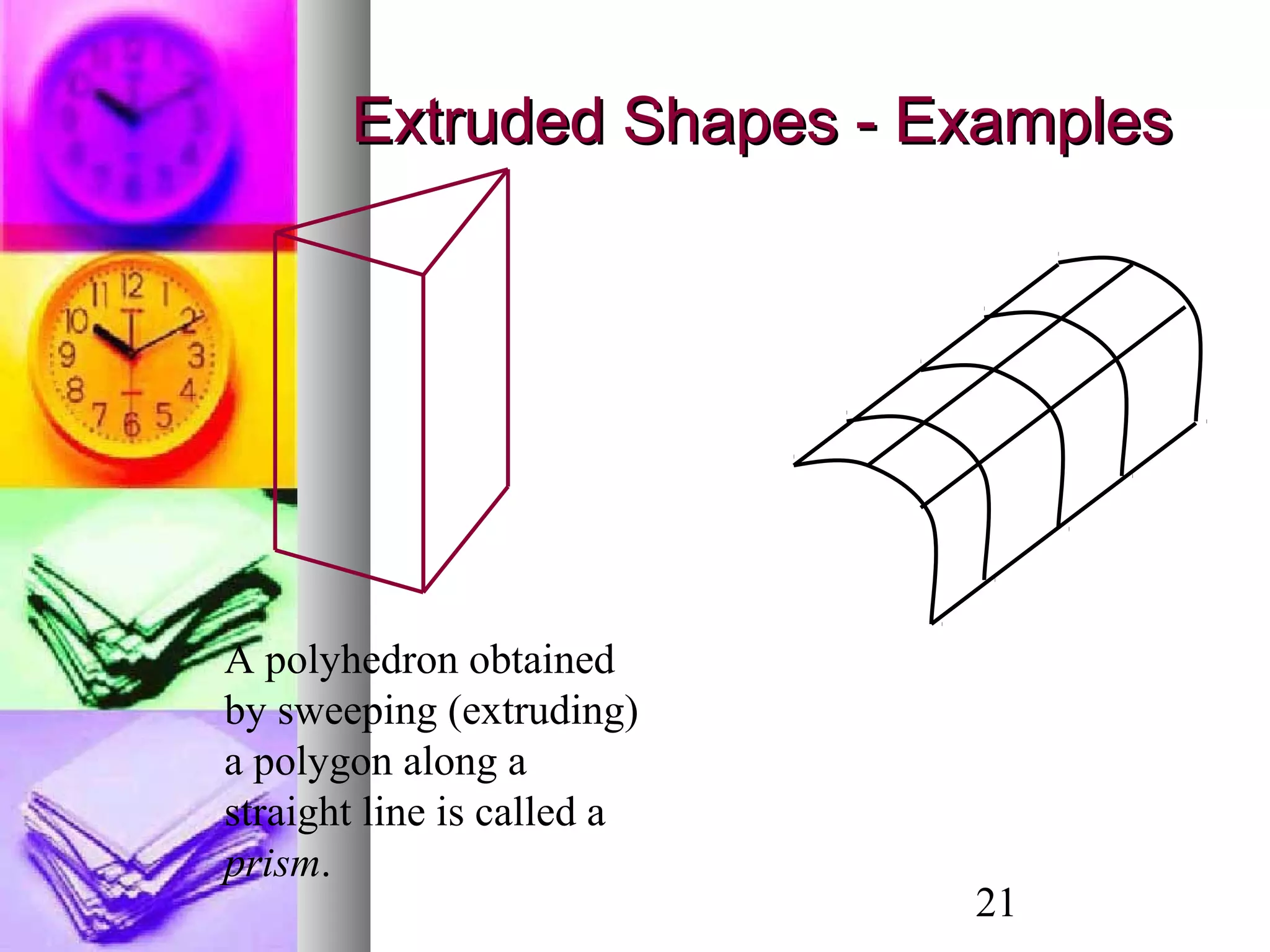
The document discusses various methods for 3D object modeling and representation, including: - Polygonal meshes which approximate surfaces and solids using polygons and can represent a broad class of objects. - Solid modeling using polygonal meshes where directional information is added to faces using normal vectors. - Sweep representations that form shapes by extruding or sweeping 2D profiles through space. 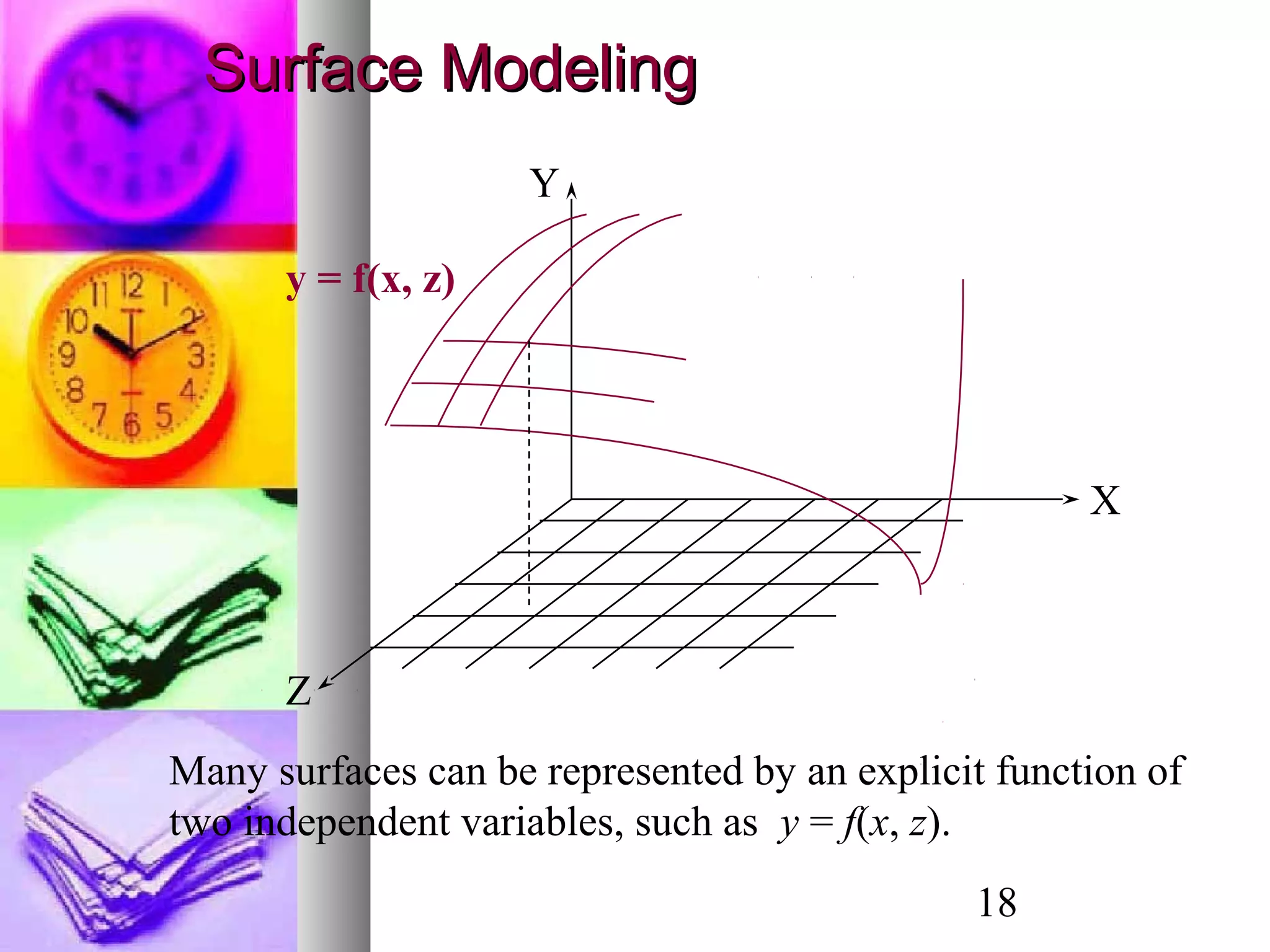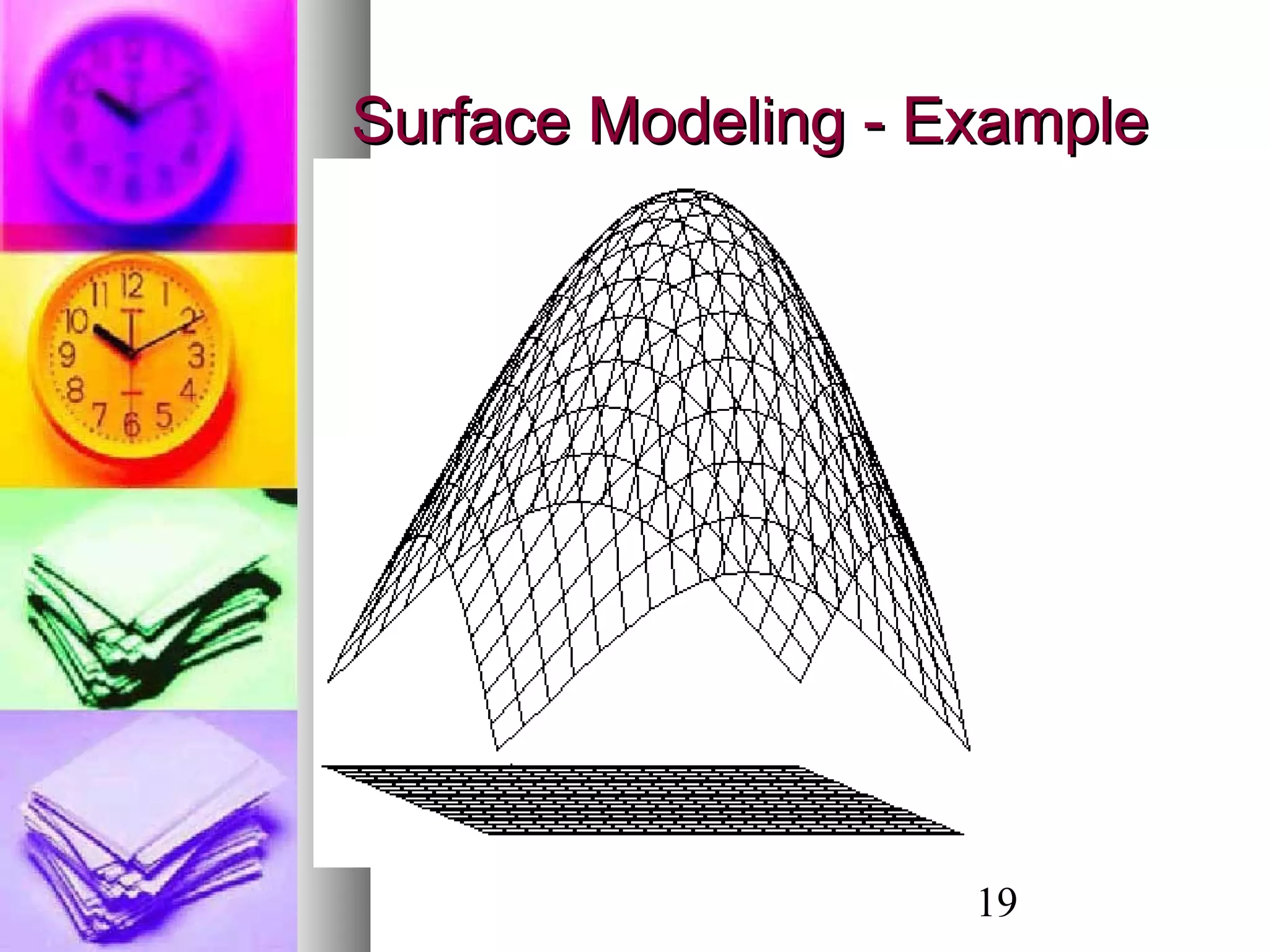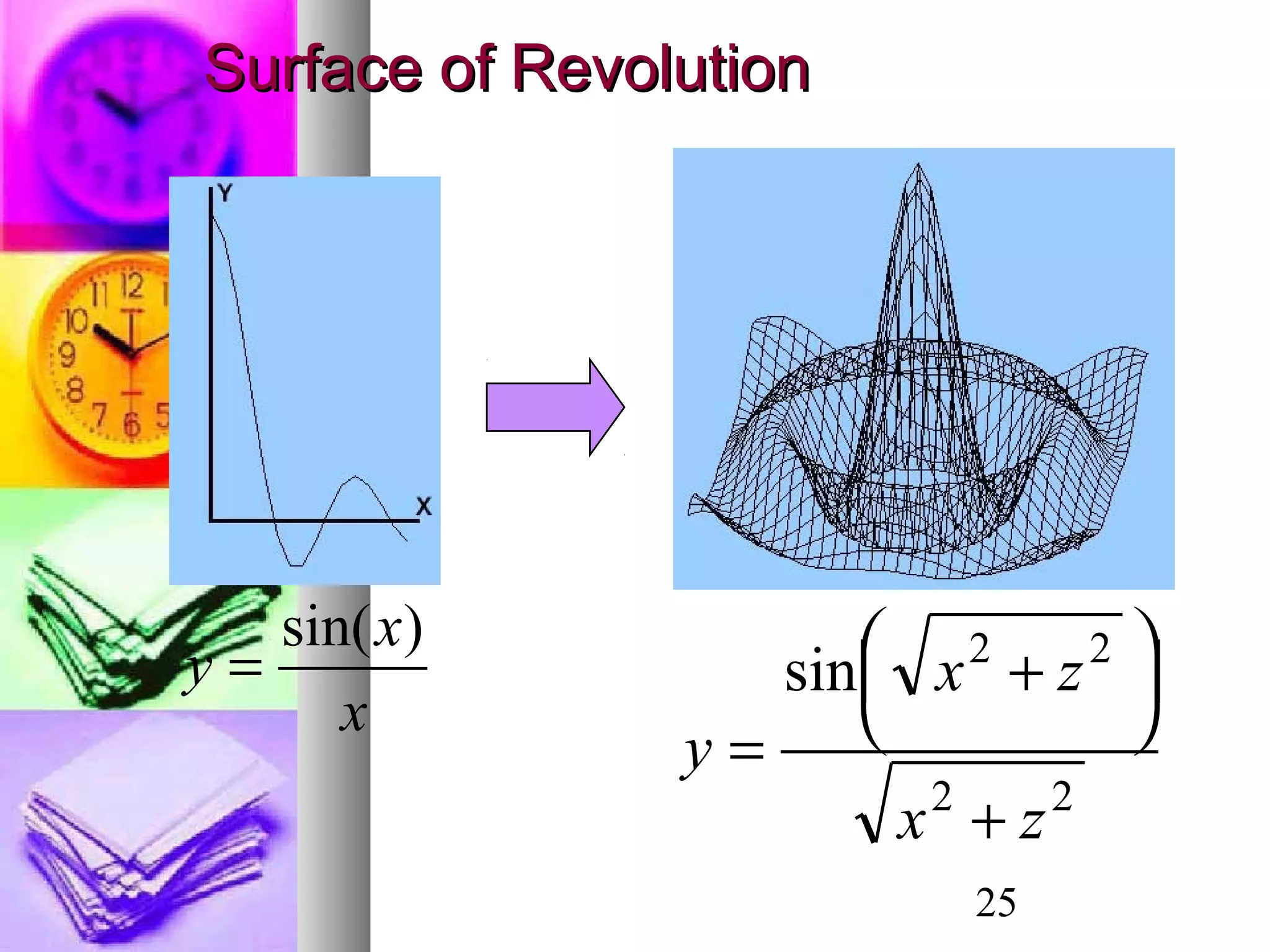- Surface modeling using explicit functions of two variables or surfaces of revolution obtained by rotating curves around axes.

1. 11
Computer GraphicsComputer Graphics
Chapter 7Chapter 7
3D Object Modeling3D Object Modeling

2. 2
3D Object Representation3D Object Representation
 A surface can be analyticallyA surface can be analytically
generated using its functiongenerated using its function
involving the coordinates.involving the coordinates.
 An object can be represented inAn object can be represented in
terms of its vertices, edges andterms of its vertices, edges and
polygons. (Wire Frame,polygons. (Wire Frame,
Polygonal Mesh etc.)Polygonal Mesh etc.)
 Curves and surfaces can also beCurves and surfaces can also be
designed using splines bydesigned using splines by
specifying a set of few controlspecifying a set of few control
points.points.
y = f(x,z)
x y z . . .

3. 3
Solid Modeling - PolyhedronSolid Modeling - Polyhedron
 A polyhedron is a connected mesh of simple planarA polyhedron is a connected mesh of simple planar
polygons that encloses a finite amount of space.polygons that encloses a finite amount of space.
 A polyhedron is a special case of a polygon mesh thatA polyhedron is a special case of a polygon mesh that
satisfies the following properties:satisfies the following properties:
 Every edge is shared by exactly two faces.Every edge is shared by exactly two faces.
 At least three edges meet at each vertex.At least three edges meet at each vertex.
 Faces do not interpenetrate. Faces at most touchFaces do not interpenetrate. Faces at most touch
along a common edge.along a common edge.
 Euler’s formulaEuler’s formula : If: If FF,, EE,, VV represent the number ofrepresent the number of
faces, vertices and edges of a polyhedron, thenfaces, vertices and edges of a polyhedron, then
VV ++ FF −− EE = 2.= 2.

4. 4
3D Object Representation3D Object Representation
 The data for polygonal meshesThe data for polygonal meshes
can be represented in two ways.can be represented in two ways.
 Method 1:Method 1:
 Vertex ListVertex List
 Normal ListNormal List
 Face List (Polygon List)Face List (Polygon List)
 Method 2:Method 2:
 Vertex ListVertex List
 Edge ListEdge List
 Face List (Polygon List)Face List (Polygon List)

5. 5
01
2 3
45
6
7
Vertices and Faces - E.g. CubeVertices and Faces - E.g. Cube
0
1
2
3
4
5
Face Index
Vertex Index

6. 6
Data representation using vertex, face and normal lists:
Vertex List Normal List Polygon List
30 30 30 0.0 0.0 1.0 0 1 2 3
-30 30 30 0.0 0.0 -1.0 4 7 6 5
-30 -30 30 0.0 1.0 0.0 0 4 5 1
30 -30 30 -1.0 0.0 0.0 1 5 6 2
30 30 -30 0.0 -1.0 0.0 2 6 7 3
-30 30 -30 1.0 0.0 0.0 3 7 4 0
-30 -30 -30
30 -30 -30

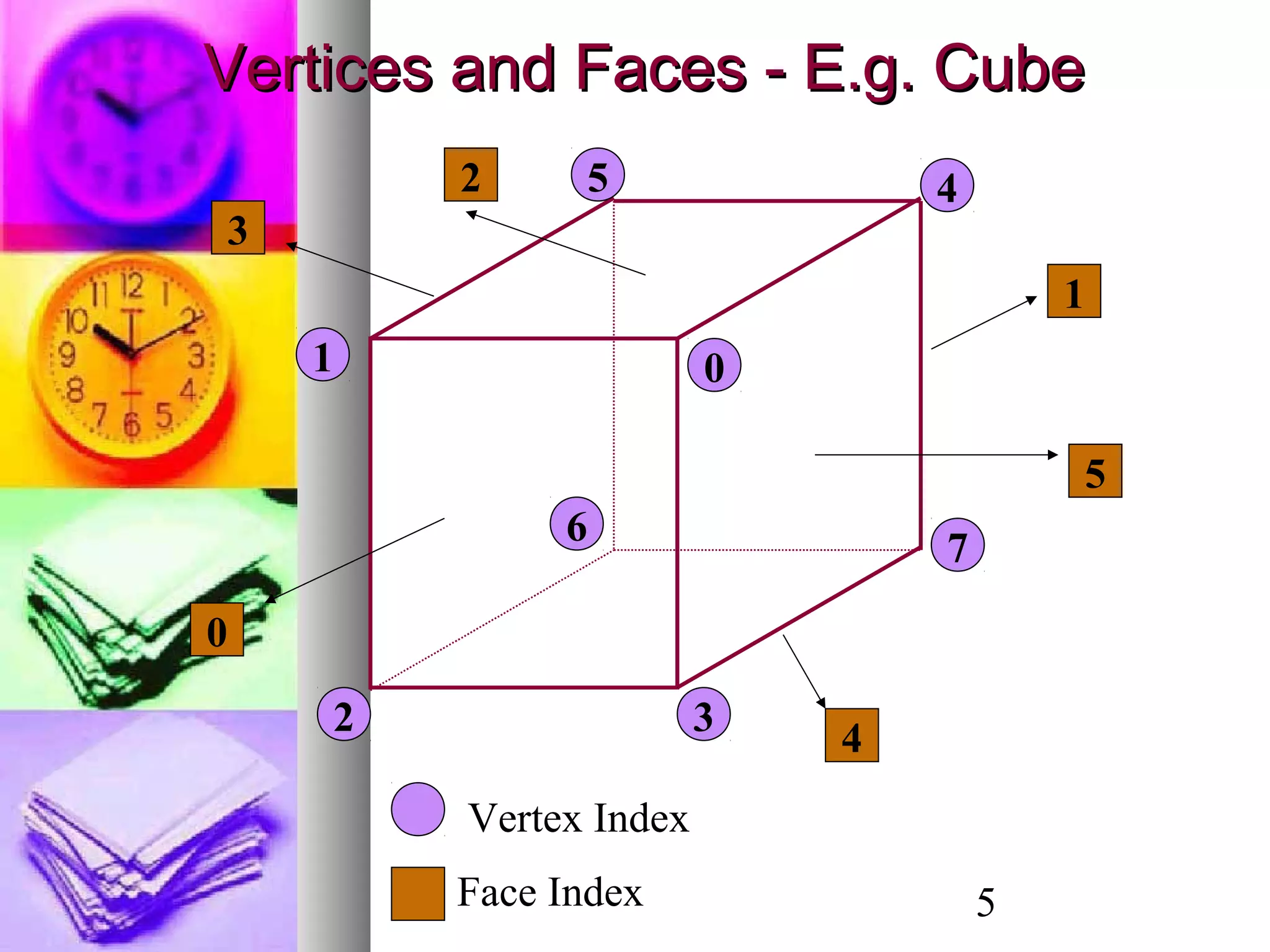
7. 7
Vertex List Edge List Polygon List
x[i] y[i] z[i] L[j] M[j] P[k] Q[k] R[k] S[k]
30 30 30 0 1 0 1 2 3
-30 30 30 1 2 4 7 6 5
-30 -30 30 2 3 0 4 5 1
30 -30 30 3 0 1 5 6 2
30 30 -30 4 5 2 6 7 3
-30 30 -30 5 6 3 7 4 0
-30 -30 -30 6 7
30 -30 -30 7 4
0 4
1 5
2 6
3 7
Data representation using vertex, face and edge lists:

8. 8
Normal Vectors (OpenGL)Normal Vectors (OpenGL)
Assigning a normal vector to a polygon:
glBegin(GL_POLYGON);
glNormal3f(xn,yn,zn);
glVertex3f(x1,y1,z1);
glVertex3f(x2,y2,z2);
glVertex3f(x3,y3,z3);
glVertex3f(x4,y4,z4);
glEnd();
Enabling automatic conversion of normal vectors to unit vectors:
glEnable(GL_NORMALIZE);

9. 9
Regular Polyhedra (Regular Polyhedra (Platonic Solids)Platonic Solids)
 If all the faces of a polyhedron areIf all the faces of a polyhedron are
identical, and each is a regular polygon,identical, and each is a regular polygon,
then the object is called athen the object is called a platonic solidplatonic solid..
 Only five such objects exist.Only five such objects exist.

10. 10
Wire-Frame ModelsWire-Frame Models
 If the object is defined only by a set of nodesIf the object is defined only by a set of nodes
(vertices), and a set of lines connecting the(vertices), and a set of lines connecting the
nodes, then the resulting objectnodes, then the resulting object
representation is called a wire-frame model.representation is called a wire-frame model.
 Very suitable for engineeringVery suitable for engineering
applications.applications.
 Simplest 3D Model - easy to construct.Simplest 3D Model - easy to construct.
 Easy to clip and manipulate.Easy to clip and manipulate.
 Not suitable for building realistic models.Not suitable for building realistic models.

11. 11
Wire Frame Models - OpenGLWire Frame Models - OpenGL
Some Wireframe Models in OpenGL:
Cube: glutWireCube(Gldouble size);
Sphere: glutWireSphere(…);
Torus: glutWireTorus(…);
Teapot: glutWireTeapot(Gldouble size);
Cone: glutWireCone(…);
(…) Refer text for list of arguments.

12. 12
Wire Frame Model - TheWire Frame Model - The
TeapotTeapot

13. 13
Polygonal MeshPolygonal Mesh
 Three-dimensional surfaces and solids can beThree-dimensional surfaces and solids can be
approximated by a set of polygonal and lineapproximated by a set of polygonal and line
elements. Such surfaces are calledelements. Such surfaces are called polygonalpolygonal
meshes.meshes.
 The set of polygons or faces, together form theThe set of polygons or faces, together form the
“skin” of the object.“skin” of the object.
 This method can be used to represent a broadThis method can be used to represent a broad
class of solids/surfaces in graphics.class of solids/surfaces in graphics.
 A polygonal mesh can be rendered using hiddenA polygonal mesh can be rendered using hidden
surface removal algorithms.surface removal algorithms.

14. 14
Polygonal Mesh - ExamplePolygonal Mesh - Example

15. 15
Solid ModelingSolid Modeling
 Polygonal meshes can be used in solidPolygonal meshes can be used in solid
modeling.modeling.
 An object is consideredAn object is considered solidsolid if theif the
polygons fit together to enclose a space.polygons fit together to enclose a space.
 In solid models, it is necessary toIn solid models, it is necessary to
incorporate directional information on eachincorporate directional information on each
face by using theface by using the normal vectornormal vector to theto the
plane of the face, and it is used in theplane of the face, and it is used in the
shading process.shading process.

16. 16
Solid Modeling - ExampleSolid Modeling - Example

17. 17
Solid Modeling - OpenGLSolid Modeling - OpenGL
Some predefined Solid Models in OpenGL:
Cube: glutSolidCube(Gldouble size);
Sphere: glutSolidSphere(…);
Torus: glutSolidTorus(…);
Teapot: glutSolidTeapot(Gldouble size);
Cone: glutSolidCone(…);
(…) Arguments same as wire-frame models.

18. 18
Z
X
Y
y = f(x, z)
Surface ModelingSurface Modeling
Many surfaces can be represented by an explicit function of
two independent variables, such as y = f(x, z).

19. 19
Surface Modeling - ExampleSurface Modeling - Example

20. 20
Sweep RepresentationsSweep Representations
 Sweep representations are useful for bothSweep representations are useful for both
surface modeling and solid modeling.surface modeling and solid modeling.
 A large class of shapes (both surfaces andA large class of shapes (both surfaces and
solid models) can be formed bysolid models) can be formed by sweepingsweeping
oror extrudingextruding a 2D shape through space.a 2D shape through space.
 Sweep representations are useful forSweep representations are useful for
constructing 3-D objects that possesconstructing 3-D objects that posses
translational or rotational symmetries.translational or rotational symmetries.

21. 21
Extruded Shapes - ExamplesExtruded Shapes - Examples
A polyhedron obtained
by sweeping (extruding)
a polygon along a
straight line is called a
prism.

22. 22
Surface of RevolutionSurface of Revolution
 A surface of revolution is obtained byA surface of revolution is obtained by
revolving a curve (known as therevolving a curve (known as the base curvebase curve
oror profile curveprofile curve) about an axis.) about an axis.
 In other words, a surface of revolution isIn other words, a surface of revolution is
generated by agenerated by a rotational sweeprotational sweep of a 2Dof a 2D
curve.curve.
 The symmetry of the surface of revolutionThe symmetry of the surface of revolution
makes it a very useful object inmakes it a very useful object in
presentation graphics.presentation graphics.

23. 23
Z
X
Y
y = f(x)
r
y y
(x, z)
y = f(r)
x
22
zxr +=
Surface of RevolutionSurface of Revolution

24. 24
The three-dimensional surface obtained by
revolving the curve y = f(x) about the y-axis is
obtained by replacing x with sqrt(x*x + z*z).
The surface of revolution is thus given by
( )y f x z= +2 2
Surface of RevolutionSurface of Revolution

25. 25
Surface of RevolutionSurface of Revolution
x
x
y
)sin(
=
22
22
sin
zx
zx
y
+





 +
=

26. 26
Quad treesQuad trees
Quad trees are generated by successivelyQuad trees are generated by successively
dividing a 2-D region(usually a square) intodividing a 2-D region(usually a square) into
quadrants. Each node in the quadtree hasquadrants. Each node in the quadtree has
4 data elements, one for each of the4 data elements, one for each of the
quadrants in the region. If all the pixelsquadrants in the region. If all the pixels
within a quadrant have the same color (awithin a quadrant have the same color (a
homogeneous quadrant), thehomogeneous quadrant), the
corresponding data element in the nodecorresponding data element in the node
stores that color. For a heterogeneousstores that color. For a heterogeneous
region of space, the successive divisionsregion of space, the successive divisions
into quadrants continues until all quadrantsinto quadrants continues until all quadrants
are homogeneous.are homogeneous.

27. 27
OctreesOctrees
 An octree encoding scheme divide regions ofAn octree encoding scheme divide regions of
3-D space(usually a cube) in to octants and3-D space(usually a cube) in to octants and
stores 8 data elements in each node of thestores 8 data elements in each node of the
tree.tree.
 Individual elements of a 3-D space are calledIndividual elements of a 3-D space are called
volume elements or voxels.volume elements or voxels.
 When all voxels in an octant are of the sameWhen all voxels in an octant are of the same
type, this type value is stored in thetype, this type value is stored in the
corresponding data element of the node. Anycorresponding data element of the node. Any
heterogeneous octant is subdivided intoheterogeneous octant is subdivided into
octants and the corresponding data elementoctants and the corresponding data element
in the node points to the next node in thein the node points to the next node in the
octree.octree.

28. 28
OctreesOctrees

29. 29
Bezier CurvesBezier Curves
The Bezier curve only approximates the control points
and doesn’t actually pass through all of them.

30. 30
Inputs: n control points (xi, yi), i = 0, 1,2, …n-1
( )
,
0
,
0
,
( ) ( )
( ) ( )
0 1
!
( ) (1 )
! !
m
b m i i
i
m
b m i i
i
i m i
m i
x u Bez u x
y u Bez u y
u
m m m
Bez u u u and
i i i m i
=
=
−
=
=
≤ ≤
   
= − = ÷  ÷
−   
∑
∑
m = n−1
Bezier CurvesBezier Curves

31. 31
Inputs: n control points (xi, yi), i = 0, 1,2, …m
0
( ) ( ) , 0 1
( ) ( ( ), ( ))
( , )
m
m i i
i i
i i i
r u Bez u r u
where
r u x u y u
r x y
=
= ≤ ≤
=
=
∑% %
%
%
Bezier CurvesBezier Curves

32. 32
Properties of Bezier CurveProperties of Bezier Curve
 Bezier curve is a polynomial ofBezier curve is a polynomial of
degree one less than thedegree one less than the
number of control pointsnumber of control points
p0
p2
p1
p0
p2
p1
p3
Quadratic Curve Cubic Curve

33. 33
Properties of Bezier Curve (cont.)Properties of Bezier Curve (cont.)
 Bezier curve always passesBezier curve always passes
through the first and last points;through the first and last points;
i.e.i.e.
andand
0(0)x x=
,
0(0)y y=
(1) mx x= (1) my y=

34. 34
Properties of Bezier CurveProperties of Bezier Curve
(cont)(cont)
 The slop at the beginning of the curve isThe slop at the beginning of the curve is
along the line joining the first two controlalong the line joining the first two control
points, and the slope at the end of thepoints, and the slope at the end of the
curve is along the line joining the last twocurve is along the line joining the last two
points.points.
p0
p2
p1
p0
p2
p1

35. 35
Properties of Bezier CurveProperties of Bezier Curve
(cont)(cont)
 Bezier blending functions are all positiveBezier blending functions are all positive
and the sum is always 1.and the sum is always 1.
 This means that the curve is the weightedThis means that the curve is the weighted
sum of the control points.sum of the control points.
,
0
( ) 1
m
m i
i
Bez u
=
=∑

36. 36
Design Technique using BezierDesign Technique using Bezier
Curves:Curves:
 A closed Bezier curve can be generated byA closed Bezier curve can be generated by
specifying the first and last control points atspecifying the first and last control points at
the same locationthe same location
p4
p0=p5
p1
p2
p3

37. 37
Design Technique (Cont)Design Technique (Cont)
 A Bezier curve can be made to pass closerA Bezier curve can be made to pass closer
to a given coordinate position by assigningto a given coordinate position by assigning
multiple control points to that position.multiple control points to that position.
p0
p1 = p2 p3
p4

38. 38
 Bezier curve can be form by piecing ofBezier curve can be form by piecing of
several Bezier section with lower degree.several Bezier section with lower degree.
p0
p1
p2= p’0
p’2
p’3
p’1

39. 39
(Not Important!)
,
0 0
( , ) ( ) ( ) ,
0 1, 0 1
( , ) ( ( , ), ( , ), ( , ))
( , , )
m l
m i l j i j
i j
ij ij ij ij
r u v Bez u Bez v r
u v
where
r u v x u v y u v z u v
r x y z
= =
=
≤ ≤ ≤ ≤
=
=
∑∑% %
%
%
Bezier SurfacesBezier Surfaces

40. 40
A set of 16 control points The Bezier Patch
Bezier PatchBezier Patch

41. 41
Utah Teapot Defined Using Control Points
Bezier PatchBezier Patch

42. 42
Utah Teapot Generated Using Bezier Patches
Bezier PatchBezier Patch