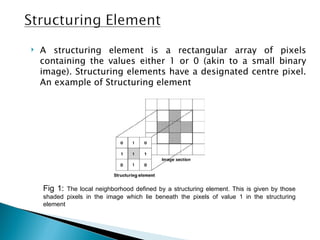
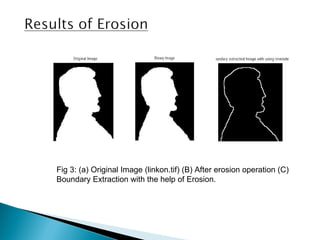
The document discusses boundary extraction techniques in image processing using mathematical morphology, specifically focusing on dilation and erosion operations. It provides definitions, mathematical formulas, and examples of MATLAB implementations for both operations, including how to create structuring elements and perform boundary extraction. Additionally, it refers to relevant literature and resources for further study in digital image processing.

1. Boundary Extraction By Dilation
and Erosion (With MatLab)
For Details: http://happystudybymaria.blogspot.com/2012/04/project-
boundary-extraction-by-dilation.html

2. Presented By:
Maria Akther
ID: 083-20-119
Dept.: Computer Science
Daffodil International University

3.  Mathematical morphology is one of the data processing
methods that is extremely useful for image processing and
has many applications, such as, boundary extraction ,noise
elimination, shape description, texture analysis, and so on.
The mathematical base of morphological processing is
dilation and erosion which are described by set analysis and
can be expressed in logical AND, OR notation .

4.  Dilation: Dilation is an operation that ‘grows’ or ‘thickens’
objects in a binary image. Mathematically, dilation is defined
in terms of set operations. The dilation of A and B is defined
as  ^

A ⊕ B = z | ( B ) z ∩ A ≠ φ
 
 Erosion: Erosion is an operation that ‘Shrinks’ or ‘thins’
objects in a binary image. The mathematical definition of
erosion of A by B is as
{
AΘB = z | ( B ) z ∩ A C ≠ φ }

5.  A structuring element is a rectangular array of pixels
containing the values either 1 or 0 (akin to a small binary
image). Structuring elements have a designated centre pixel.
An example of Structuring element
Fig 1: The local neighborhood defined by a structuring element. This is given by those
shaded pixels in the image which lie beneath the pixels of value 1 in the structuring
element

6.  In Matlab, to construct the structuring element array by
using ‘strel’ function. The example below illustrates how
Matlab displays when a strel object is created:
>> se= strel (’disk, 3’); % A disk of radius 3
Which displays the matrix as follows:

7.  Erosion Algorithm: The boundary of a set A, denoted by
β(A), can be obtained by first eroding A by B and then
performing the set differences between A and its erosion. That
is,
β(A)=A – (AΘB)
Dilation Algorithm: The boundary of a set A, denoted by
β(A), can be obtained by first dilating A by B and then
performing the set differences between A and its dilation. That
⊕
is,
β(A)= (A B) – A

8.  Dilation Operation: Five-pixel-long diagonal line with the origin
at the center
 When the structuring element overlaps 1-valued pixels, the pixel
at the origin is marked 1. In Matlab, we can carry out image
dilation using the Image Processing Toolbox functions “imdilate”.
>>imdilate_image = imdilate(Orginal_binary_image,structuring_element_array);

9. Fig 2: (a) Original Image (linkon.tif) (B) After Dilation Operation (C)
Boundary Extraction with the help of Dilation.

10.  Erosion Operation: a three-pixel-long vertical line
with the origin at the center
 In Matlab, we can carry out image erosion using the
Image Processing Toolbox functions “imerode”.
>>imerode_image = imerode(Orginal_binary_image , structuring_element_array);

11. Fig 3: (a) Original Image (linkon.tif) (B) After erosion operation (C)
Boundary Extraction with the help of Erosion.

12.  Boundary Extraction with the help of Dilation:
A=imread('linkon.tif');
s=strel('disk',3);%Structuring element
F=imdilate(A,s); %Dialte the image by structuring element
figure,imshow(A);title('Original Image');
figure,imshow(F);title('Imdilate Image');
figure,imshow(F-A);title('Boundary extracted Image with using imdilate');
 Boundary Extraction with the help of Erosion:
A=imread('linkon.tif');
s=strel('disk',3); %Structuring element
F=imerode(A,s); %Erode the image by structuring element
figure,imshow(A); title('Original Image');
figure,imshow(A-F); title('Boundary extracted Image with using imerode');

13. 1. "Fundamentals of Digital Image Processing", Chris Solomon and
Toby Breckon, Wiley Publications. 1st edition.
2. “Digital Image Processing Using Matlab”, Rafael C. Gonzalez,
Richard E. Woods and Steven L. Eddins, 2nd edition.
3. “Discrete Mathematics”, Seymour Lipschutz and Marc Lars Lipson,
2nd edition, Mcgraw-hill publication.
4. Images can be downloaded from:
http://www.imageprocessingplace.com/DIP-3E/dip2e_book_images_dow

14. Thanks To All