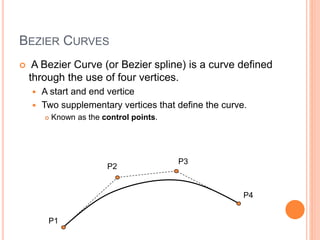
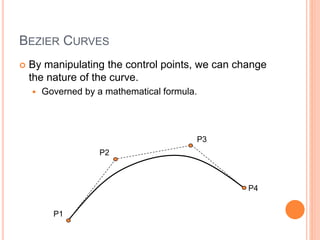
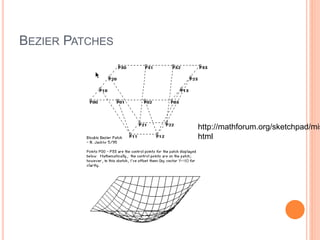
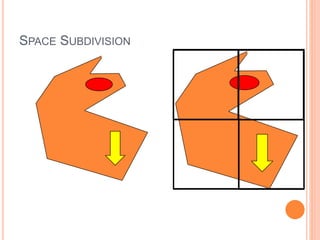
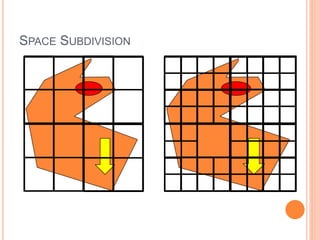
The document discusses various techniques for representing 3D graphics beyond polymeshes, including Bezier curves, Bezier patches, NURBS, constructive solid geometry (CSG), and space subdivision. Each method is described with its advantages, drawbacks, and applications, highlighting how the choice of representation affects the intended use and efficiency. The lecture emphasizes the mathematical modeling and control points involved in shaping these graphical representations.

1. GRAPHICAL REPRESENTATION
Michael Heron

2. INTRODUCTION
 In the last lecture we talked about the processes we
go through to build a 3D object.
 We focused primarily on the polymesh.
 In this lecture we are going to look at alternate
representations.
 Bezier curves
 Bezier Patches
 NURBS surfaces
 Constructive Solid Geometry

3. BEZIER CURVES
 A Bezier Curve (or Bezier spline) is a curve defined
through the use of four vertices.
 A start and end vertice
 Two supplementary vertices that define the curve.
 Known as the control points.
P1
P2
P3
P4

4. BEZIER CURVES
 By manipulating the control points, we can change
the nature of the curve.
 Governed by a mathematical formula.
P1
P2
P3
P4

5. BEZIER CURVES
 Bezier curves are used for:
 Modelling smooth curves
 In a way that cannot be done with a polymesh
 Curves appear smooth at all scales
 Font representation
 Vector/Outline fonts
 Animation
 Used to define smooth, realistic paths for movement.

6. BEZIER PATCHES
 Related to the idea of a Bezier curve is a Bezier
patch.
 Curves are 2D, patches are 3D
 Bezier patches are shaped nets, the appearance of
which are determined by control points.
 Control points act like gravity spots on underlying
shape.
 The define the topology of the shape through mathematical
modelling of attraction

7. BEZIER PATCHES
http://mathforum.org/sketchpad/mis
html

8. BEZIER PATCHES
 Bezier patches offer several advantages
 Integrity of representation
 Continuity across boundaries
 Awareness of neighbours
 Fluid representation
 Exact representation
 Can measure volumes and surfaces
 Economical
 A single patch can represent many polygonal equivalents.

9. BEZIER PATCHES
 However, they also have drawbacks.
 Simple patch has 16 control points.
 Rendering with a Bezier patch is expensive.
 Around 10 times slower than equivalent polymesh
 But this does not take into account the difference in time
requirements to model a polymesh correctly.
 Large number of perspectives required to render
properly.

10. NURBS
 Non-Uniform Rational B-Splines
 Yikes!
 Extension of the idea of a Bezier curve
 Defined by control points.
 Each control point has a weight
 Defines how much that control point influences the
curve.
 NURBS have knots
 Vectors that describe how the resulting curve is
influenced by the control points.
 NURBS have an order
 How closely the curve follows the lines between control
points.

11. CONSTRUCTIVE SOLID GEOMETRY
 Complex shapes modeled by using simple shapes.
 To these shapes we add or subtract other simple
shapes.
 Combination of shapes using boolean operators
and set theory allows for new and interesting
complex topographies.
 Unions, Intersections, etc

12. CSG EXAMPLES
Images here show boolean operations – union, intersection, and
difference.
http://www.student.cs.uwaterloo.ca/~cs488/Contrib/f02/a5/djbigham/

13. INTERSECTIONS
 When two primitives intersect, the new object is the
volume shared by both shapes

14. DIFFERENCE
 Difference is all the bits that don’t intersect.

15. UNION
 A union is both shapes together.
 A merge, in other words.
 The new object can be treated as a single new
shape
 And be transformed as a holistic unit.

16. VOXEL REPRESENTATION
 Sometimes need to represent 3D space as voxels.
 3D Pixels
 3D space broken up into three dimensional arrays
of voxels.
 Each voxel labeled according to its object
occupancy.

17. VOXEL REPRESENTATION
 Voxel arrays are:
 Costly in terms of memory
 Entire object space must be separated down into cubic
elements
 Labelled according to object occupancy
 Space subdivision
 Frequently used in:
 Game representations of terrain
 Medical imagery
 Ray tracing

18. SPACE SUBDIVISION
 Process of space subdivision common to 2D and
3D graphics.
 Easier to understand in 3D.
 Start with a 1x1 square representing entire image.
 Then recursively subdivide squares.
 Stop when each pixel inside a subdivided square
has a single colour.

19. SPACE SUBDIVISION

20. SPACE SUBDIVISION

21. VOLUME SUBDIVISON
 Works the same way in 3D as in 2D
 We start with cubes
 Recursive subdivide cubes
 From our cube, subdivide into eight smaller cubes.
 Can represent space/volume subdivision as a tree
data structure.
 Easy to navigate and store
 Offers greater efficiency of representation.
 Advancement over simple voxel array.

22. SUMMARY
 Various ways to represent 3D graphics beyond
polymeshes.
 Bezier Curves
 Bezier Patches
 NURBS
 CSG
 Space Subdivision
 Each technique has its real life applications.
 The nature of the intended destination will dictate the
appropriate tool.