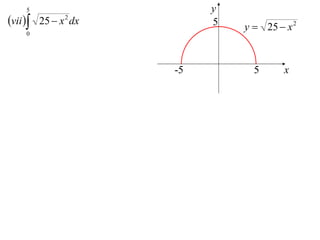
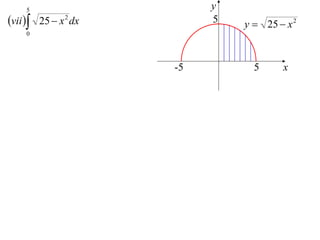
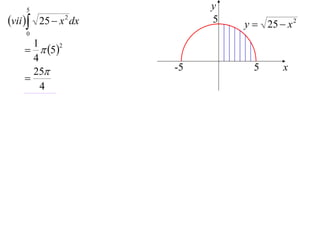
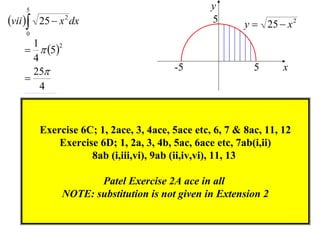
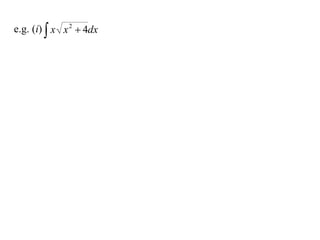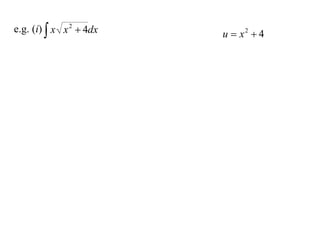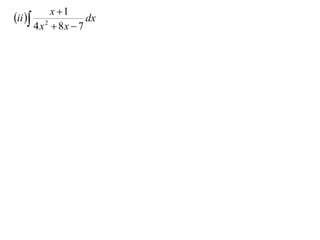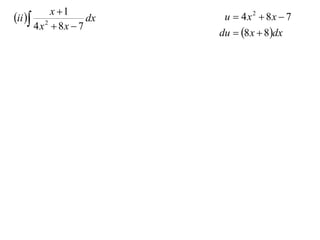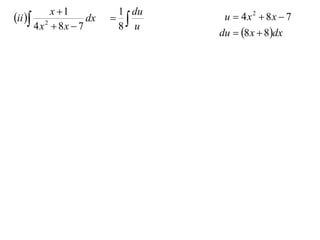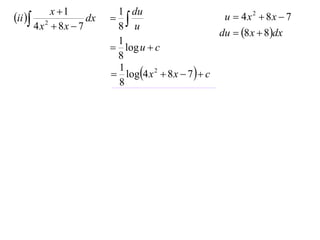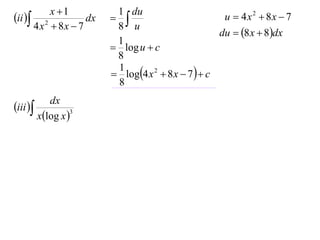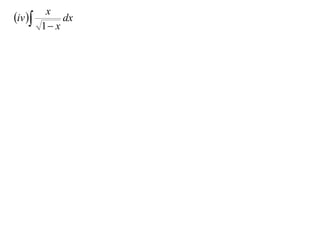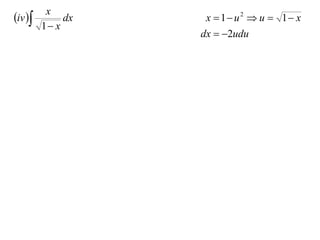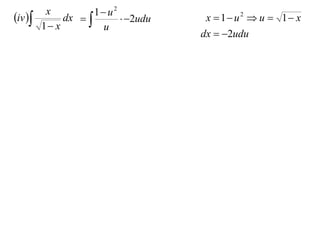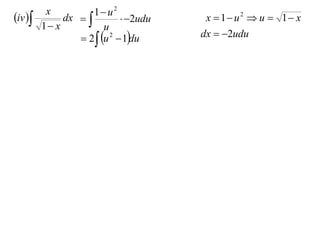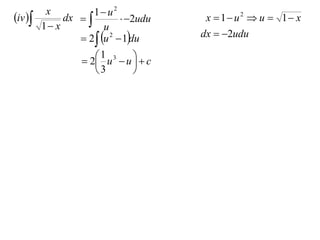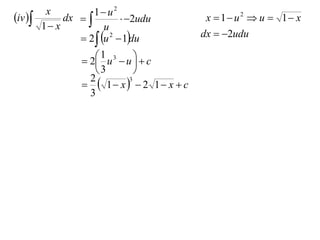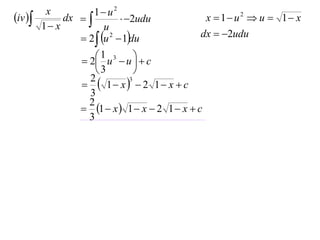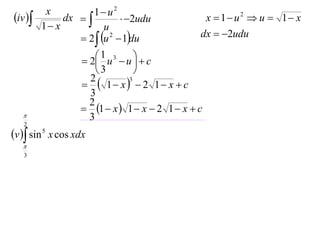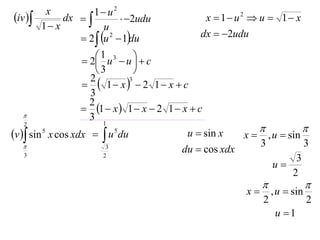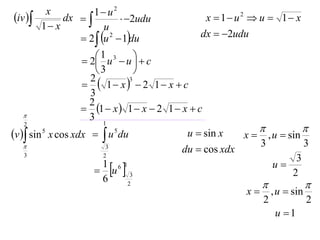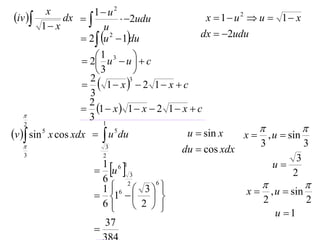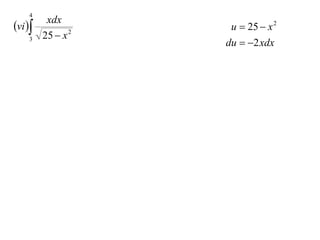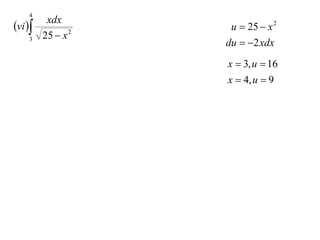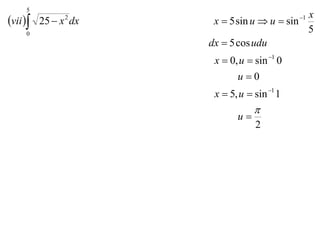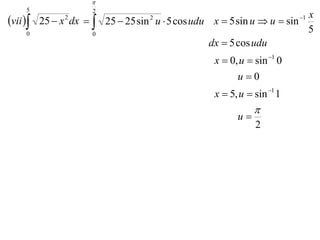The document discusses the technique of integration using substitution to convert integrals into standard forms. Various standard integrals are presented, including those involving power functions, exponential functions, and trigonometric functions. The text provides examples and methods for calculating integrals using substitutions effectively.

1. Integration Using
Substitution

2. Integration Using
Substitution
Try to convert the integral into a “standard integral”

3. Integration Using
Substitution
Try to convert the integral into a “standard integral”
STANDARD INTEGRALS
1 n 1
 x dx  x , n  1; x  0, if n  0
n
n 1

4. Integration Using
Substitution
Try to convert the integral into a “standard integral”
STANDARD INTEGRALS
1 n 1
 x dx  x , n  1; x  0, if n  0
n
n 1
1
 xdx  ln x, x  0

5. Integration Using
Substitution
Try to convert the integral into a “standard integral”
STANDARD INTEGRALS
1 n 1
 x dx  x , n  1; x  0, if n  0
n
n 1
1
 xdx  ln x, x  0

6. Integration Using
Substitution
Try to convert the integral into a “standard integral”
STANDARD INTEGRALS
1 n 1
 x dx  x , n  1; x  0, if n  0
n
n 1
1
 xdx  ln x, x  0
1
 e ax dx  e ax , a  0
a

7. Integration Using
Substitution
Try to convert the integral into a “standard integral”
STANDARD INTEGRALS
1 n 1
 x dx  x , n  1; x  0, if n  0
n
n 1
1
 xdx  ln x, x  0
1
 e ax dx  e ax , a  0
a
1
 cos ax dx  sin ax, a  0
a

8. Integration Using
Substitution
Try to convert the integral into a “standard integral”
STANDARD INTEGRALS
1 n 1
 x dx  x , n  1; x  0, if n  0
n
n 1
1
 xdx  ln x, x  0
1
 e ax dx  e ax , a  0
a
1
 cos ax dx  sin ax, a  0
a
1
 sin ax dx   cos ax, a  0
a

9. 1
 sec  tan ax, a  0
2
ax dx
a

10. 1
 sec  tan ax, a  0
2
ax dx
a
1
 sec ax tan ax dx  sec ax, a  0
a

11. 1
 sec  tan ax, a  0
2
ax dx
a
1
 sec ax tan ax dx  sec ax, a  0
a
1 1 1 x
 a 2  x 2 dx  tan
a a
, a0

12. 1
 sec  tan ax, a  0
2
ax dx
a
1
 sec ax tan ax dx  sec ax, a  0
a
1 1 1 x
 a 2  x 2 dx  tan
a a
, a0
1 x
 a 2  x 2 dx  sin 1 , a  0,  a  x  a
a

13. 1
 sec  tan ax, a  0
2
ax dx
a
1
 sec ax tan ax dx  sec ax, a  0
a
1 1 1 x
 a 2  x 2 dx  tan
a a
, a0
1 x
 a 2  x 2 dx  sin 1 , a  0,  a  x  a
a
1
 x 2  a 2 dx  
 ln x  x 2  a 2 , x  a  0

14. 1
 sec  tan ax, a  0
2
ax dx
a
1
 sec ax tan ax dx  sec ax, a  0
a
1 1 1 x
 a 2  x 2 dx  tan
a a
, a0
1 x
 a 2  x 2 dx  sin 1 , a  0,  a  x  a
a
1
 x 2  a 2 dx  
 ln x  x 2  a 2 , x  a  0

1
x a
2 2
dx 
 ln x  x 2  a 2 

15. e.g. (i)  x x 2  4dx

16. e.g. (i)  x x 2  4dx u  x2  4

17. e.g. (i)  x x 2  4dx u  x2  4
u

18. e.g. (i)  x x 2  4dx u  x2  4
du  2 xdx
u

19. e.g. (i)  x x 2  4dx u  x2  4
1 du  2 xdx
du u
2

20. e.g. (i)  x x 2  4dx  1 2 x x 2  4dx
2 u  x2  4
1 1 2
1 du  2 xdx
2
du u   u du
2

21. e.g. (i)  x x 2  4dx  1 2 x x 2  4dx
2 u  x2  4
1 1 2
1 du  2 xdx
2
du u   u du
2
3
1 2 2
  u c
2 3

22. e.g. (i)  x x 2  4dx  1 2 x x 2  4dx
2 u  x2  4
1 1 2
1 du  2 xdx
2
du u   u du
2
3
1 2 2
  u c
2 3
3
1 2
 u c
3

23. e.g. (i)  x x 2  4dx  1 2 x x 2  4dx
2 u  x2  4
1 1 2
1 du  2 xdx
2
du u   u du
2
3
1 2 2
  u c
2 3
3
1 2
 u c
3
 x  4 2  c
3
1 2
3

24. e.g. (i)  x x 2  4dx  1 2 x x 2  4dx
2 u  x2  4
1 1 2
1 du  2 xdx
2
du u   u du
2
3
1 2 2
  u c
2 3
3
1 2
 u c
3
 x  4 2  c
3
1 2
3
 x  4  x 2  4  c
1 2
3

25. x 1
ii  dx
4 x  8x  7
2

26. x 1
ii  dx u  4x2  8x  7
4 x  8x  7
2
du  8 x  8dx

27. x 1 1 du
ii 
8 u
dx  u  4x2  8x  7
4 x  8x  7
2
du  8 x  8dx

28. x 1 1 du
ii 
8 u
dx  u  4x2  8x  7
4 x  8x  7
2
du  8 x  8dx
1
 log u  c
8

29. x 1 1 du
ii 
8 u
dx  u  4x2  8x  7
4 x  8x  7
2
du  8 x  8dx
1
 log u  c
8
 log4 x 2  8 x  7   c
1
8

30. x 1 1 du
ii 
8 u
dx  u  4x2  8x  7
4 x  8x  7
2
du  8 x  8dx
1
 log u  c
8
 log4 x 2  8 x  7   c
1
8
dx
iii 
xlog x 
3

31. x 1 1 du
ii 
8 u
dx  u  4x2  8x  7
4 x  8x  7
2
du  8 x  8dx
1
 log u  c
8
 log4 x 2  8 x  7   c
1
8
dx
iii  u  log x
xlog x 
3
dx
du 
x

32. x 1 1 du
ii 
8 u
dx  u  4x2  8x  7
4 x  8x  7
2
du  8 x  8dx
1
 log u  c
8
 log4 x 2  8 x  7   c
1
8
dx du
iii   3 u  log x
xlog x 
3
u
dx
  u du
3
du 
x

33. x 1 1 du
ii 
8 u
dx  u  4x 2  8x  7
4 x  8x  7
2
du  8 x  8dx
1
 log u  c
8
 log4 x 2  8 x  7   c
1
8
dx du
iii   3 u  log x
xlog x 
3
u
dx
  u du
3
du 
x
1 2
  u c
2
1
  2 c
2u

34. x 1 1 du
ii 
8 u
dx  u  4x 2  8x  7
4 x  8x  7
2
du  8 x  8dx
1
 log u  c
8
 log4 x 2  8 x  7   c
1
8
dx du
iii   3 u  log x
xlog x 
3
u
dx
  u du
3
du 
x
1 2
  u c
2
1
  2 c
2u
1
 c
2log x 
2

35. x
iv  dx
1 x

36. x
iv  dx x  1 u2  u  1 x
1 x
dx  2udu

37. x 1 u2
iv  dx    2udu x  1 u2  u  1 x
1 x u
dx  2udu

38. x 1 u2
iv  dx    2udu x  1 u2  u  1 x
1 x u
 2  u 2  1du dx  2udu

39. x 1 u2
iv  dx    2udu x  1 u2  u  1 x
1 x u
 2  u 2  1du dx  2udu
 1 u3  u   c
 2 
 3 

40. x 1 u2
iv  dx    2udu x  1 u2  u  1 x
1 x u
 2  u 2  1du dx  2udu
 1 u3  u   c
 2 
 3 
  1 x  2 1 x  c
2 3
3

41. x 1 u2
iv  dx    2udu x  1 u2  u  1 x
1 x u
 2  u 2  1du dx  2udu
 2 1 u3  u   c

 3 
  1 x  2 1 x  c
2 3
3
2
 1  x  1  x  2 1  x  c
3

42. x 1 u2
iv  dx    2udu x  1 u2  u  1 x
1 x u
 2  u 2  1du dx  2udu
 2 1 u3  u   c

 3 
  1 x  2 1 x  c
2 3
3
2
 1  x  1  x  2 1  x  c
 3
2
v  sin 5 x cos xdx

3

43. x 1 u2
iv  dx    2udu x  1 u2  u  1 x
1 x u
 2  u 2  1du dx  2udu
 2 1 u3  u   c

 3 
  1 x  2 1 x  c
2 3
3
2
 1  x  1  x  2 1  x  c
 3
2
v  sin 5 x cos xdx u  sin x

3
du  cos xdx

44. x 1 u2
iv  dx    2udu x  1 u2  u  1 x
1 x u
 2  u 2  1du dx  2udu
 2 1 u3  u   c

 3 
  1 x  2 1 x  c
2 3
3
2
 1  x  1  x  2 1  x  c
 3
2
 
v  sin 5 x cos xdx u  sin x x  , u  sin
3 3

3
du  cos xdx
3
u
2

45. x 1 u2
iv  dx    2udu x  1 u2  u  1 x
1 x u
 2  u 2  1du dx  2udu
 2 1 u3  u   c

 3 
  1 x  2 1 x  c
2 3
3
2
 1  x  1  x  2 1  x  c
 3
2
 
v  sin 5 x cos xdx u  sin x x  , u  sin
3 3

3
du  cos xdx
3
u
2
 
x , u  sin
2 2
u 1

46. x 1 u2
iv  dx    2udu x  1 u2  u  1 x
1 x u
 2  u 2  1du dx  2udu
 2 1 u3  u   c

 3 
  1 x  2 1 x  c
2 3
3
2
 1  x  1  x  2 1  x  c
 3 1
2
 
v  sin 5 x cos xdx   u 5 du u  sin x x  , u  sin
3 3

3 2
3
du  cos xdx
3
u
2
 
x , u  sin
2 2
u 1

47. x 1 u2
iv  dx    2udu x  1 u2  u  1 x
1 x u
 2  u 2  1du dx  2udu
 2 1 u3  u   c

 3 
  1 x  2 1 x  c
2 3
3
2
 1  x  1  x  2 1  x  c
 3 1
2
 
v  sin 5 x cos xdx   u 5 du u  sin x x  , u  sin
3 3

3 2
3
du  cos xdx
3
 u  3
1 61 u
2
6 2  
x , u  sin
2 2
u 1

48. x 1 u2
iv  dx    2udu x  1 u2  u  1 x
1 x u
 2  u 2  1du dx  2udu
 2 1 u3  u   c

 3 
  1 x  2 1 x  c
2 3
3
2
 1  x  1  x  2 1  x  c
 3 1
2
 
v  sin 5 x cos xdx   u 5 du u  sin x x  , u  sin
3 3

3 2
3
du  cos xdx
3
 u  3
1 61 u
2
6
1 6 2  3 6 
  
 1     x , u  sin
6 2 2
  2   u 1
37


49. 4
xdx
vi 
3 25  x 2

50. 4
xdx
vi  u  25  x 2
25  x 2
3
du  2 xdx

51. 4
xdx
vi  u  25  x 2
25  x 2
3
du  2 xdx
x  3, u  16
x  4, u  9

52. 4 9
xdx
vi  1 du
  u  25  x 2
25  x 2
2 16 u
3
du  2 xdx
16 1
1 

29 u du 2
x  3, u  16
x  4, u  9

53. 4 9
xdx
vi  1 du
  u  25  x 2
25  x 2
2 16 u
3
du  2 xdx
16 1
1 

29 u du 2
x  3, u  16
x  4, u  9
1 16
 
 u  2
 9

54. 4 9
xdx
vi  1 du
  u  25  x 2
25  x 2
2 16 u
3
du  2 xdx
16 1
1 

29 u du 2
x  3, u  16
x  4, u  9
1 16
 
 u  2
 9
 16  9
1

55. 5
vii  25  x 2 dx
0

56. 5
x
vii  25  x dx
2 1
x  5 sin u  u  sin
0
5
dx  5 cos udu

57. 5
x
vii  25  x dx
2
x  5 sin u  u  sin 1
0
5
dx  5 cos udu
x  0, u  sin 1 0
u0
x  5, u  sin 1 1

u
2

58. 
5 2
x
vii  25  x dx  
2
25  25 sin u  5 cos udu x  5 sin u  u  sin
2 1
0 0
5
dx  5 cos udu
x  0, u  sin 1 0
u0
x  5, u  sin 1 1

u
2

59. 
5 2
x
vii  25  x dx   25  25 sin u  5 cos udu x  5 sin u  u  sin
2 2 1
0 0
5
2 dx  5 cos udu
  25 cos u  5 cos udu
2
0
x  0, u  sin 1 0
 u0
2
 25 cos 2 udu x  5, u  sin 1 1
0

u
2

60. 
5 2
x
vii  25  x dx   25  25 sin u  5 cos udu x  5 sin u  u  sin
2 2 1
0 0
5
2 dx  5 cos udu
  25 cos u  5 cos udu
2
0
x  0, u  sin 1 0
 u0
2
 25 cos 2 udu x  5, u  sin 1 1
0
 
2
u
25 2
  1  cos 2u du
2 0

25  1 2
 u  sin 2u 
2  2 0

61. 
5 2
x
vii  25  x dx   25  25 sin u  5 cos udu x  5 sin u  u  sin
2 2 1
0 0
5
2 dx  5 cos udu
  25 cos u  5 cos udu
2
0
x  0, u  sin 1 0
 u0
2
 25 cos 2 udu x  5, u  sin 1 1
0
 
2
u
25 2
  1  cos 2u du
2 0

25  1 2
 u  sin 2u 
2  2 0
25  1 
   sin   0
2 2 2 
25

4

62. 5
vii  25  x 2 dx
0

63. 5 y
vii  25  x 2 dx 5 y  25  x 2
0
-5 5 x

64. 5 y
vii  25  x 2 dx 5 y  25  x 2
0
-5 5 x

65. 5 y
vii  25  x 2 dx 5 y  25  x 2
0
1
  5
2
4
25 -5 5 x

4

66. 5 y
vii  25  x 2 dx 5 y  25  x 2
0
1
  5
2
4
25 -5 5 x

4
Exercise 6C; 1, 2ace, 3, 4ace, 5ace etc, 6, 7 & 8ac, 11, 12
Exercise 6D; 1, 2a, 3, 4b, 5ac, 6ace etc, 7ab(i,ii)
8ab (i,iii,vi), 9ab (ii,iv,vi), 11, 13
Patel Exercise 2A ace in all
NOTE: substitution is not given in Extension 2