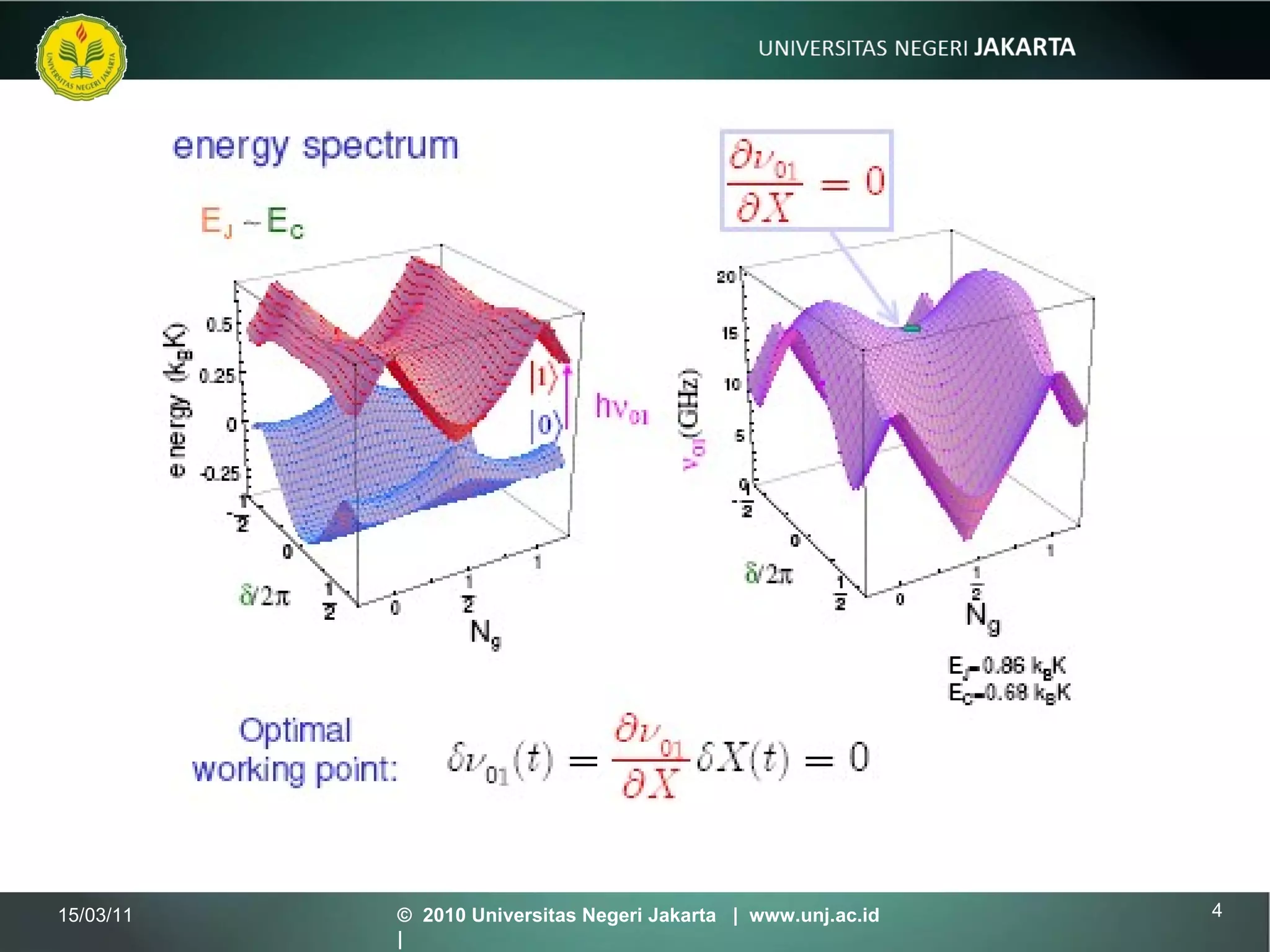
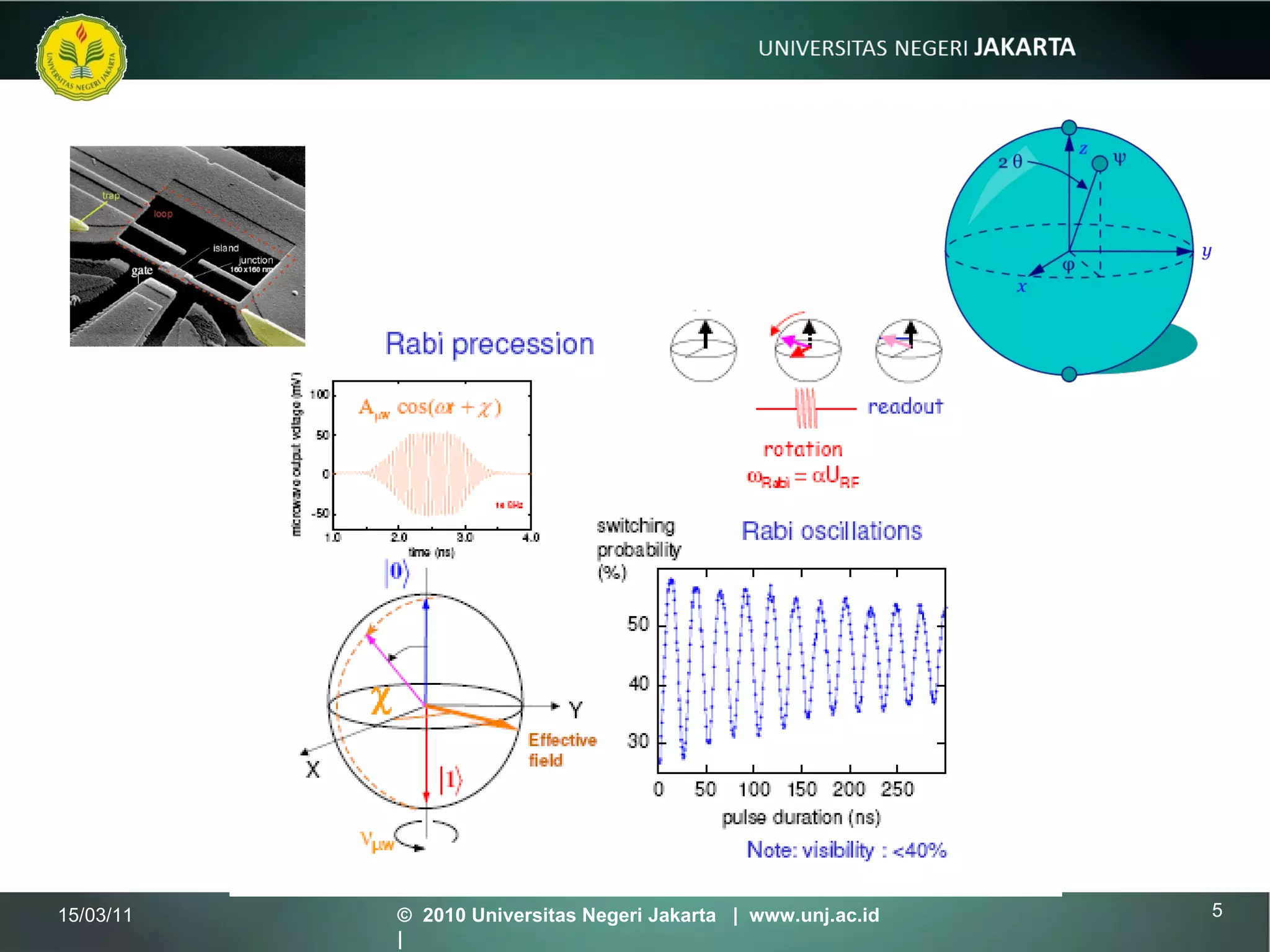
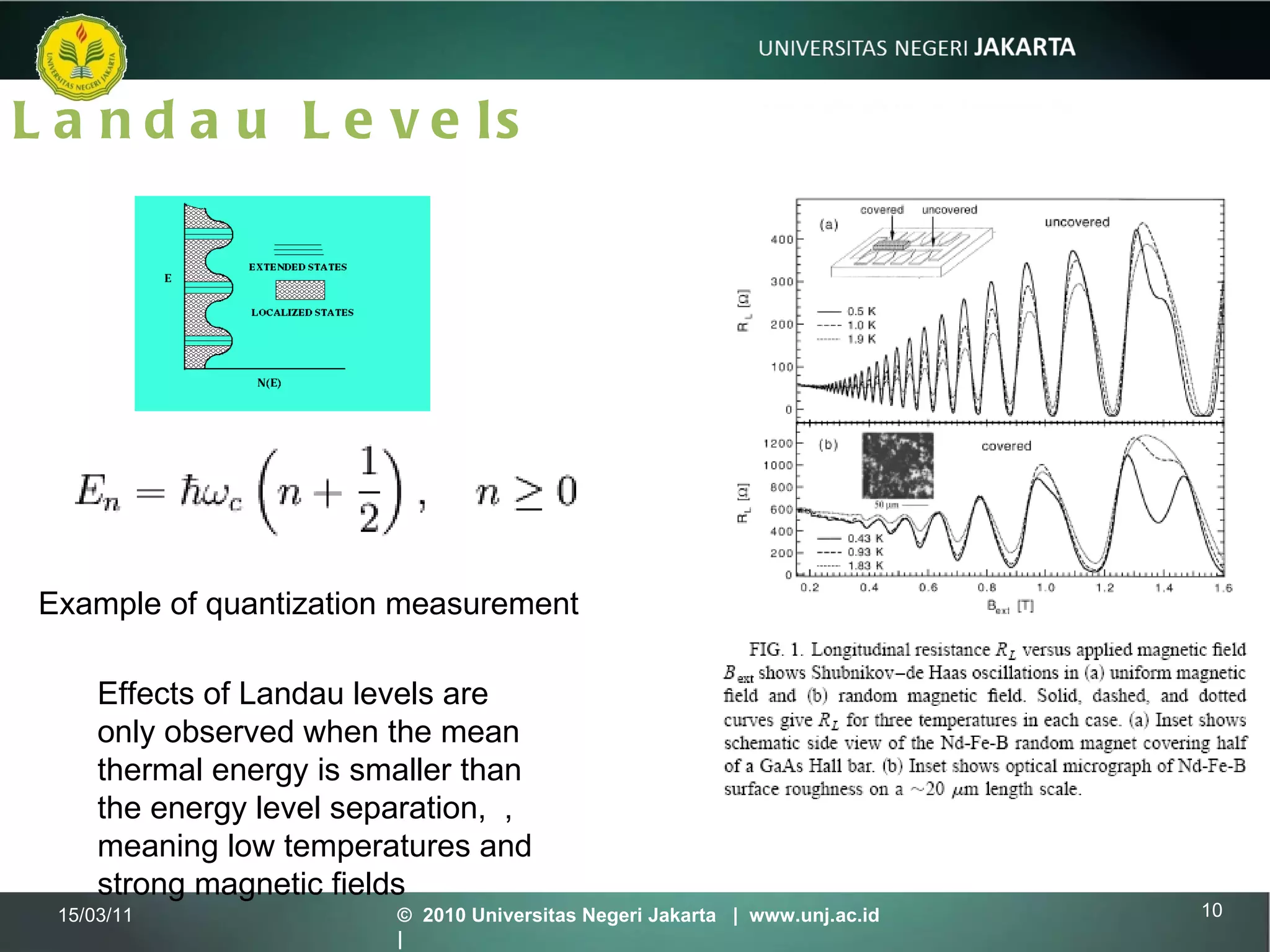
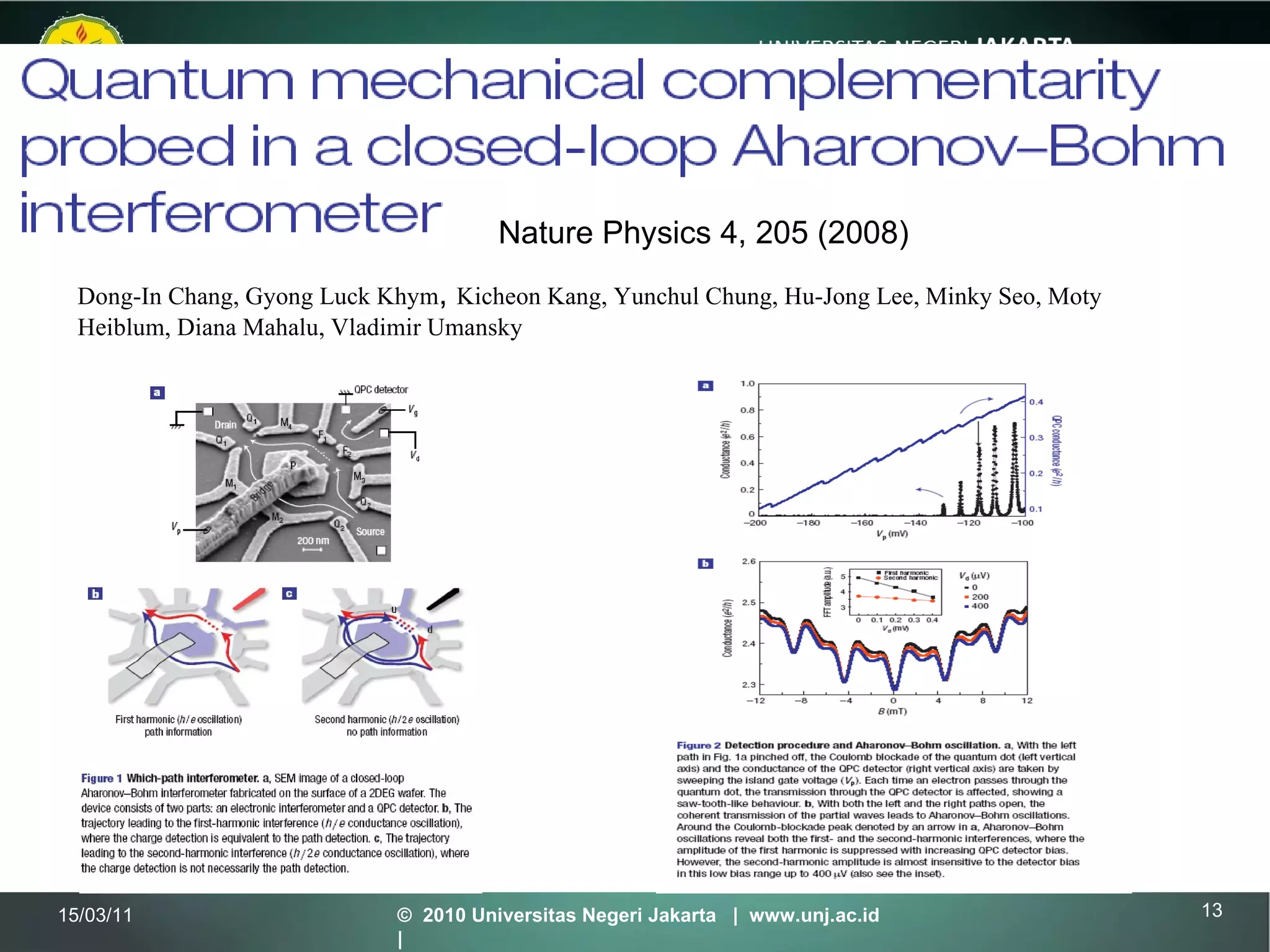
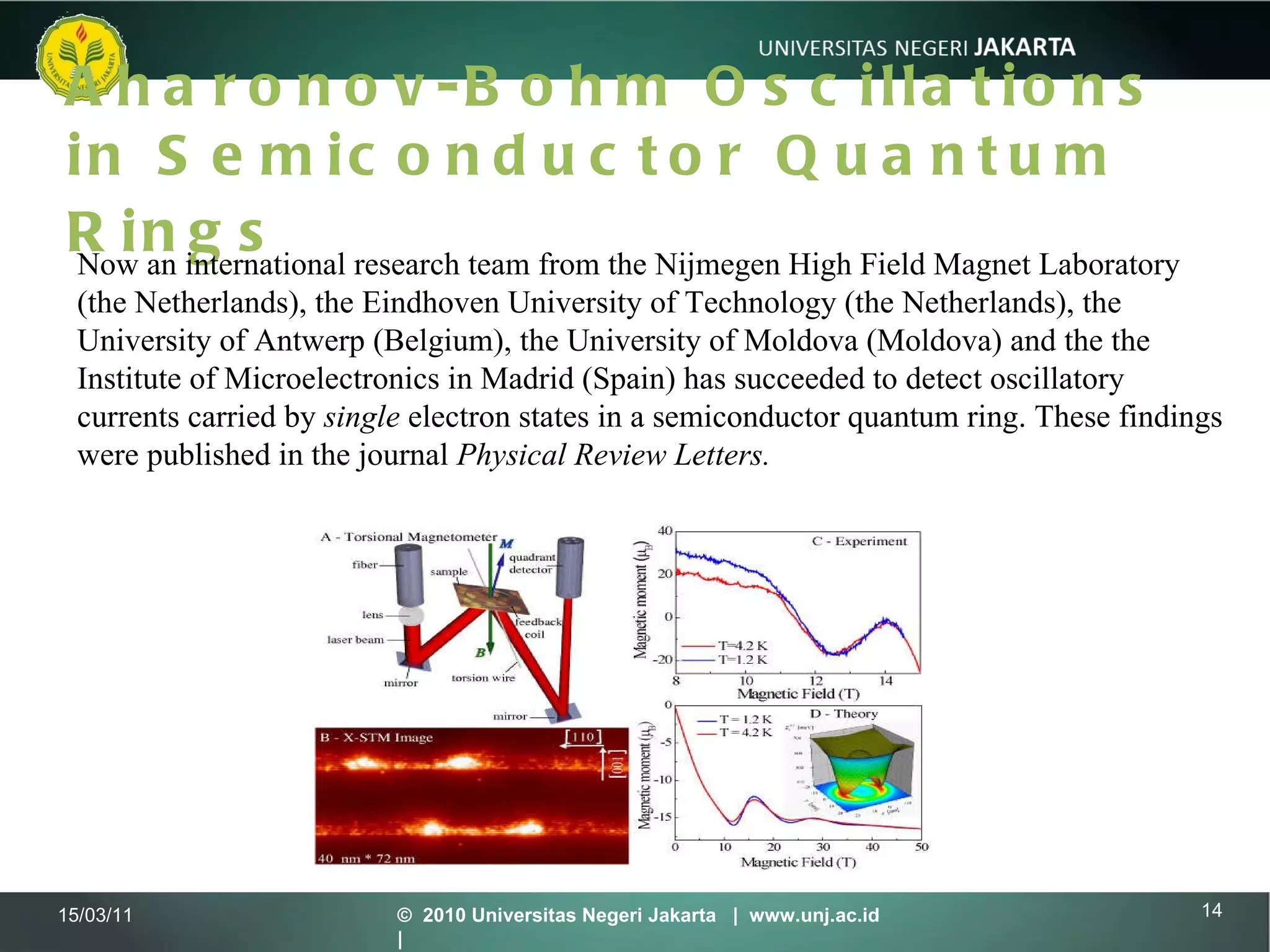
The document discusses several topics in quantum mechanics including: 1) The time-dependent transition amplitude of electrons in magnetic fields and the Aharonov-Bohm effect. 2) Quantizing the motion of electrons confined to a plane in a uniform perpendicular magnetic field using Landau levels. 3) Observing Aharonov-Bohm oscillations in semiconductor quantum rings caused by magnetic flux through the ring area.

1. Pertemuan 12 - 14 FISIKA ZAT PADAT EFEK MAGNETIK DALAM MEKANIKA KUANTUM Iwan Sugihartono, M.Si Jurusan Fisika Fakultas Matematika dan Ilmu Pengetahuan Alam

2. Outline Time dependent transition amplitude Electron in a magnetic field Aharonov Bohm effect and its applications 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

3. Two levels system 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id | | cb ( t ) | 2 = cos(ω t )2 where ω is the Rabi frequency

4. 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

5. 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

6. Classical Electrodynamics micro/macroscopic electric field micro/macroscopic magnetic field charge/current density Constitutive equations 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id | Potentials Charge conservation polarization magnetization speed of light

7. Energy & momentum Point charge: , Lorentz force Energy balance in a space domain EM energy density Kinetic energy of charges Poynting’s energy flux vector 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id | using identity

8. Electron in a Magnetic field 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id | Quantization P change to P op and r to r op Wave function Lev_Davidovich_Landau

9. 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id | is easy to check that To actually solve Schrödinger’s equation for an electron confined to a plane in a uniform perpendicular magnetic field, it is convenient to use the Landau gauge. ) . H commutes with px , so H and px have a common set of eigenstates, taking

10. Landau Levels 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id | Example of quantization measurement Effects of Landau levels are only observed when the mean thermal energy is smaller than the energy level separation, , meaning low temperatures and strong magnetic fields

11. Aharonov Bohm 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id | The Aharonov-Bohm effect demonstrates that the electromagnetic potentials, rather than the electric and magnetic fields, are the fundamental quantities in quantum mechanics. The necessary conditions to observe the Aharonov-Bohm effect, i.e. a shift of the diffraction pattern that varies periodically with B , are: There must be at least two interfering alternatives for the particle to arrive at the detector, and At least two of these interfering alternatives must enclose a shielded magnetic field and must be topologically distinct. The animation shows the superposition of the waves for the case with (in blue) and without (in red) a magnetic field.

12. Magnetic Aharonov Bohm effect Result of the requirement that quantum physics be invariant with respect to the gauge choice for the vector potential A. This implies that a particle with electric charge q traveling along some path P in a region with zero magnetic field must acquire a phase which is in si units: phase difference between any two paths with the same endpoints therefore determined by the magnetic flux Φ through the area between the paths is given by: 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

13. 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id | Dong-In Chang, Gyong Luck Khym , Kicheon Kang, Yunchul Chung, Hu-Jong Lee, Minky Seo, Moty Heiblum, Diana Mahalu, Vladimir Umansky Nature Physics 4, 205 (2008)

14. Aharonov-Bohm Oscillations in Semiconductor Quantum Rings 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id | Now an international research team from the Nijmegen High Field Magnet Laboratory (the Netherlands), the Eindhoven University of Technology (the Netherlands), the University of Antwerp (Belgium), the University of Moldova (Moldova) and the the Institute of Microelectronics in Madrid (Spain) has succeeded to detect oscillatory currents carried by single electron states in a semiconductor quantum ring. These findings were published in the journal Physical Review Letters.

15. THANK YOU 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |