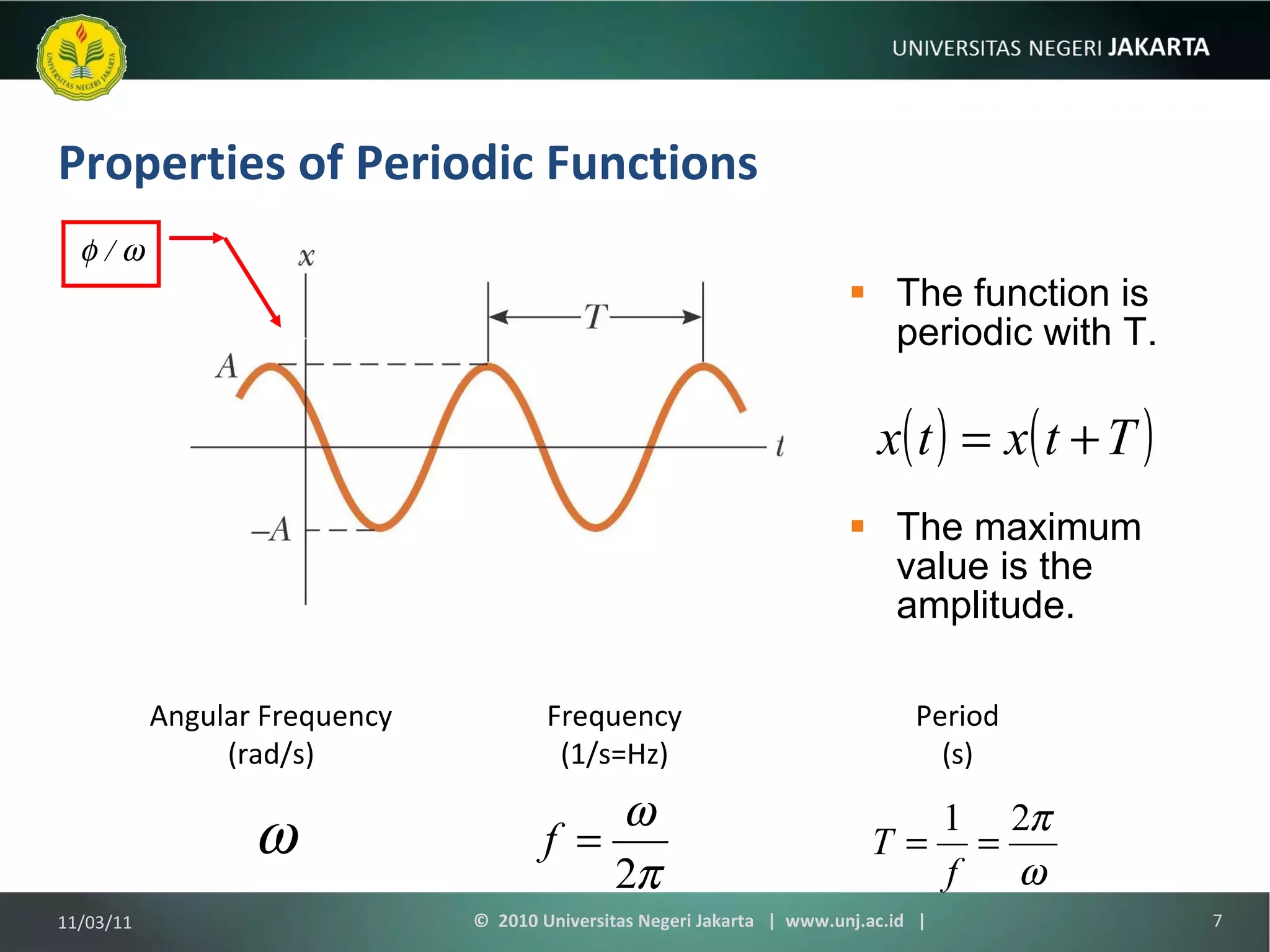
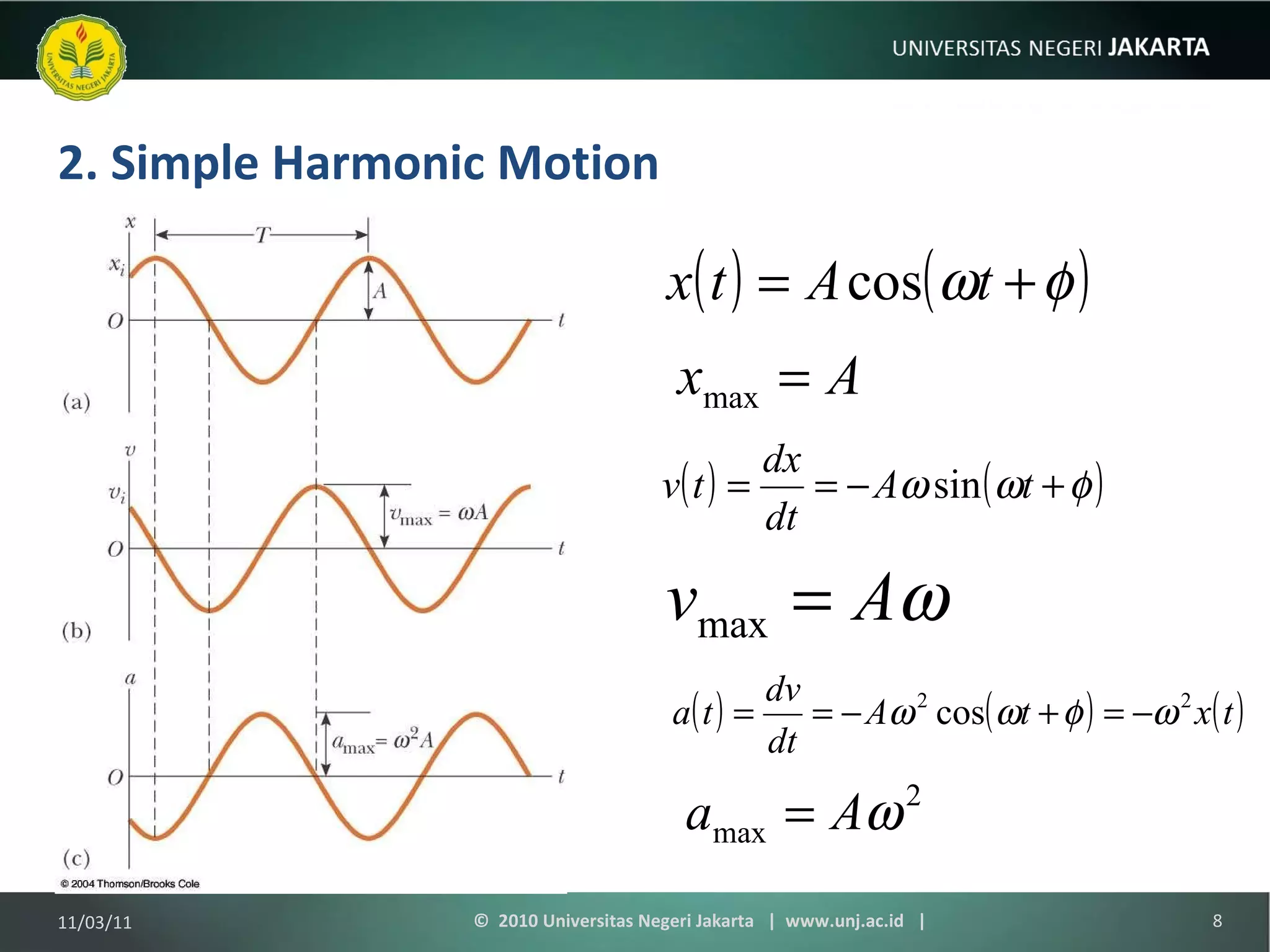
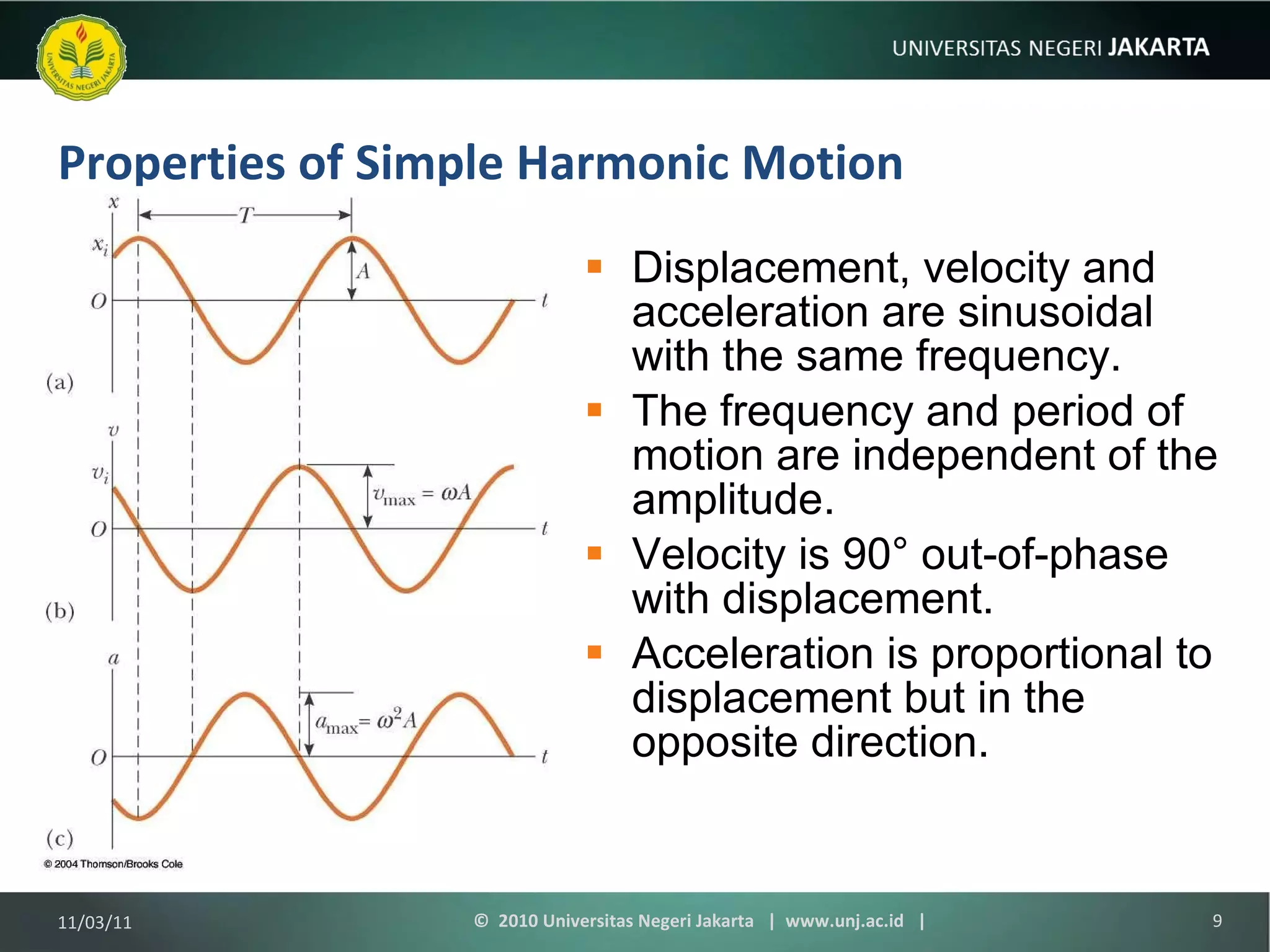
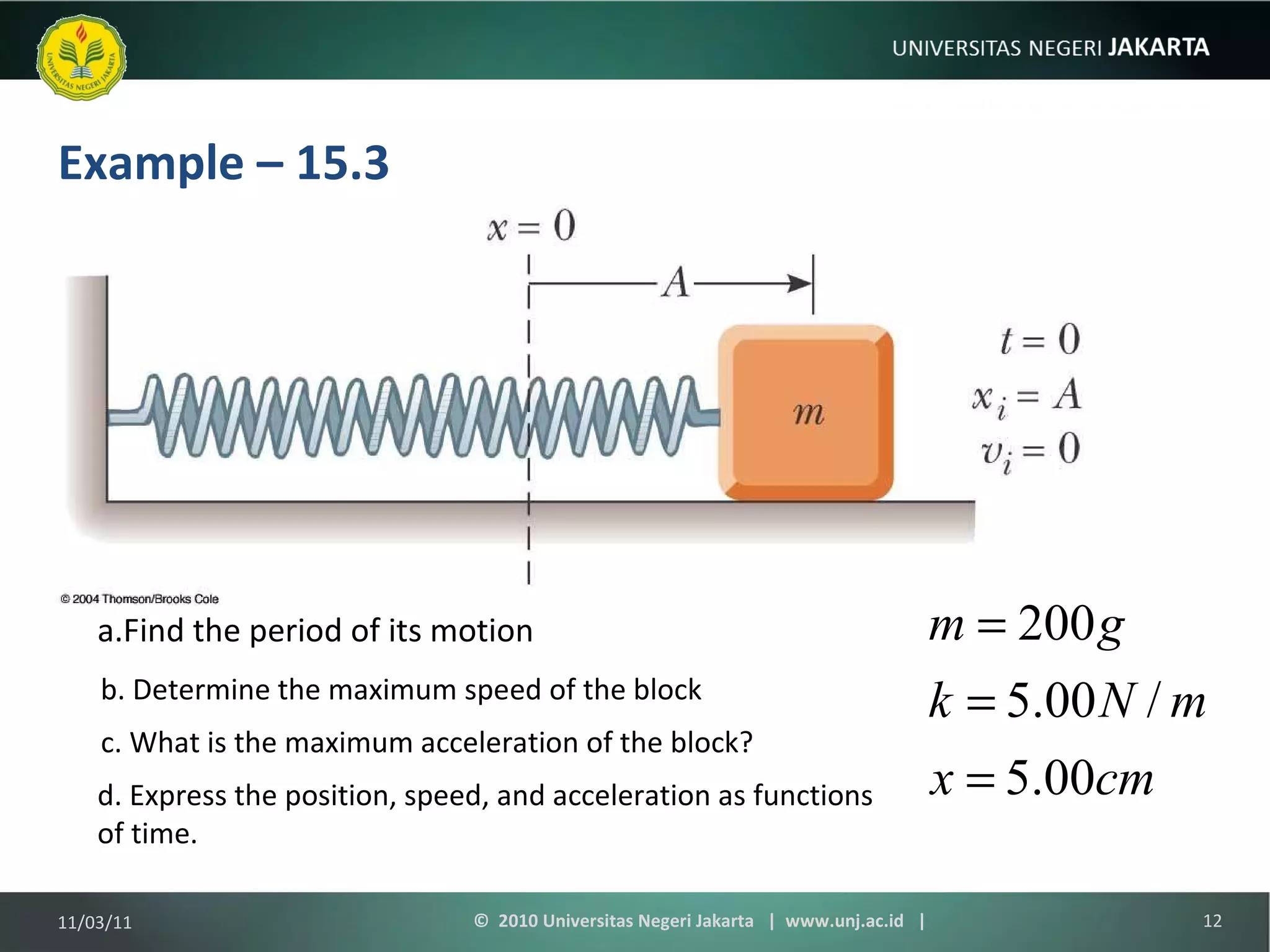
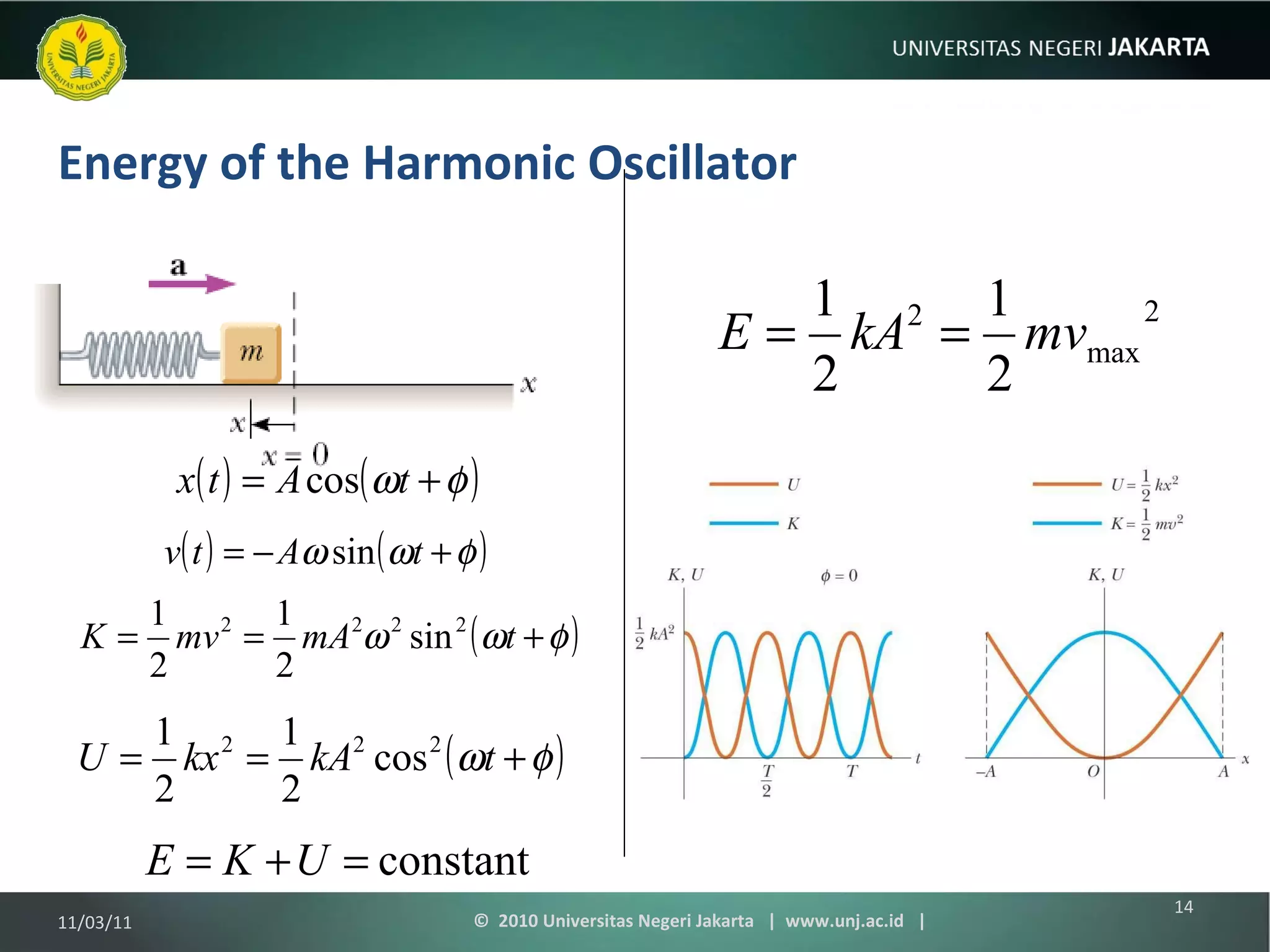
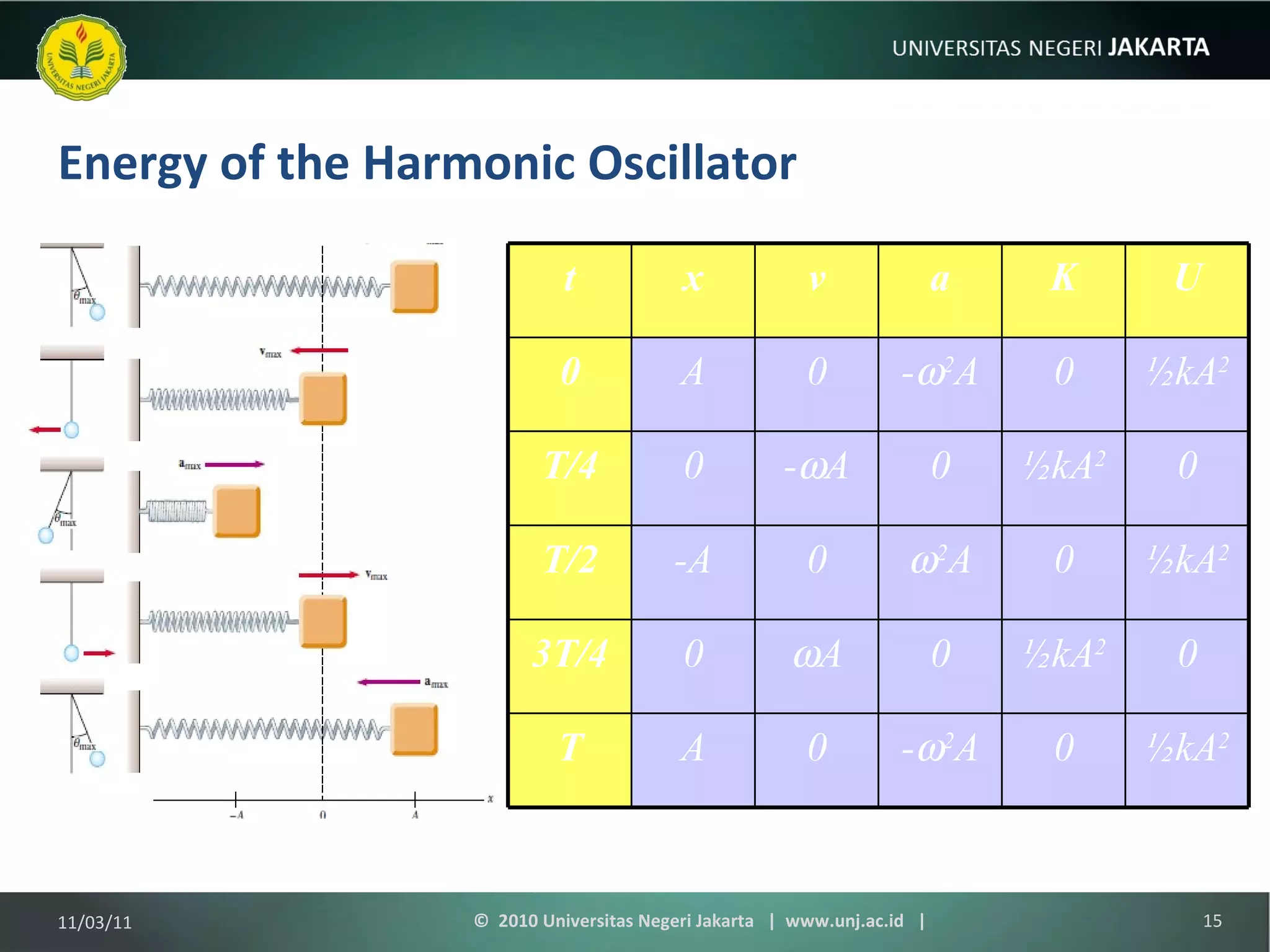
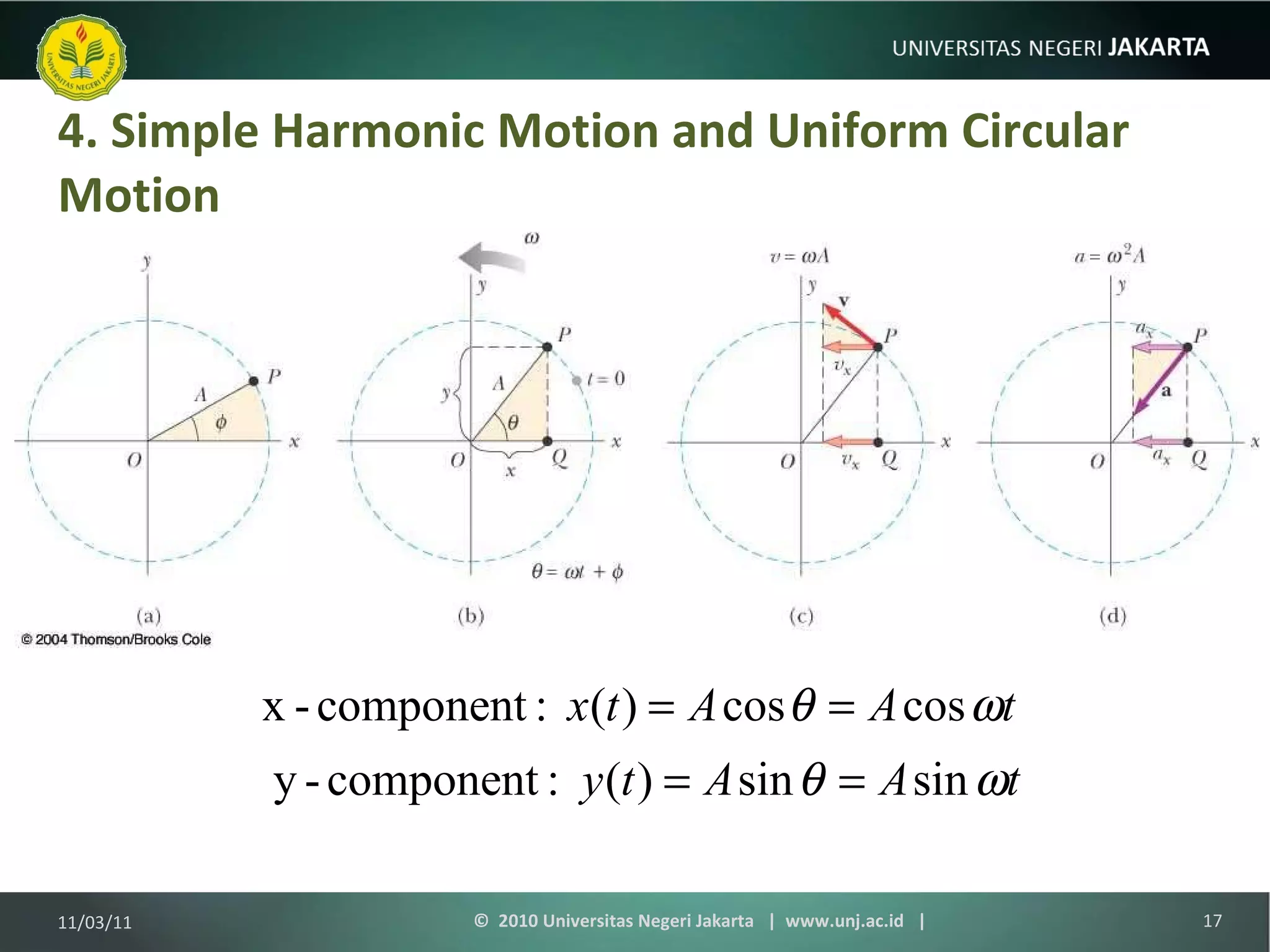
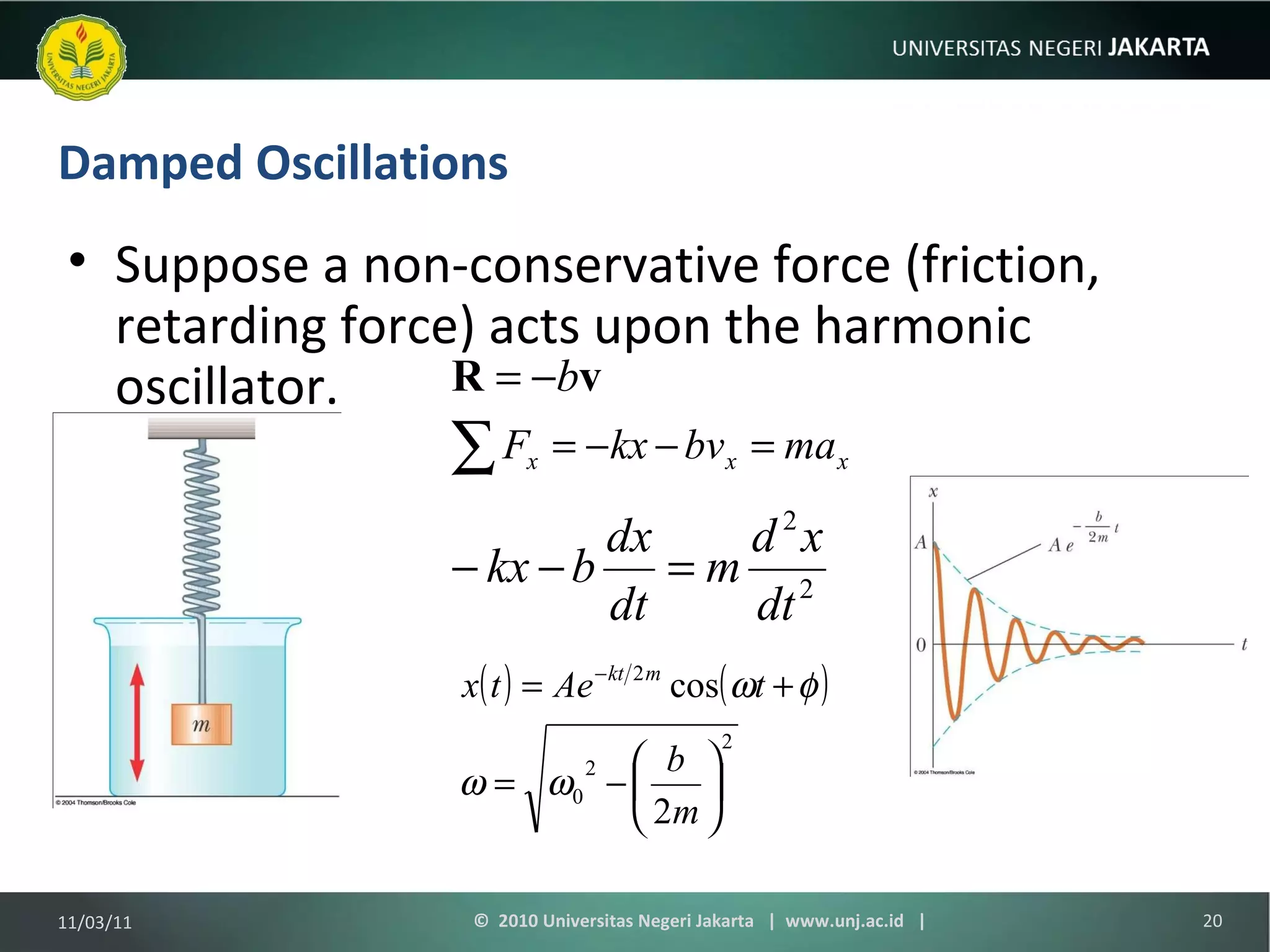
The document discusses simple harmonic motion and oscillations. It covers objects attached to springs, the equations of motion, energy of harmonic oscillators, circular motion, pendulums, and damped oscillations. Examples are provided to illustrate key concepts like calculating period, velocity, acceleration, and energy of oscillating systems. Terminology around simple harmonic motion like amplitude, angular frequency, and phase are also defined.

4. 1. An Object Attached to a Spring When acceleration is proportional to and in the opposite direction of the displacement from equilibrium, the object moves with Simple Harmonic Motion . 11/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

5. Equation of Motion Second order differential equation for the motion of the block The harmonic solution for the spring-block system where 11/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

6. Some Terminology Amplitude Angular frequency Phase constant Phase } 11/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

8. 2. Simple Harmonic Motion 11/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

11. The Block-Spring System Frequency is only dependent on the mass of the object and the force constant of the spring 11/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

12. Example – 15.3 a.Find the period of its motion b. Determine the maximum speed of the block c. What is the maximum acceleration of the block? d. Express the position, speed, and acceleration as functions of time. 11/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

14. Energy of the Harmonic Oscillator 11/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

15. Energy of the Harmonic Oscillator 11/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id | t x v a K U 0 A 0 -  2 A 0 ½kA 2 T/4 0 -  A 0 ½kA 2 0 T/2 -A 0  2 A 0 ½kA 2 3T/4 0  A 0 ½kA 2 0 T A 0 -  2 A 0 ½kA 2

17. 4. Simple Harmonic Motion and Uniform Circular Motion 11/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

18. 5. The Simple Pendulum The tangential component of the gravitational force is a restoring force For small  (  < 10°): The form as simple harmonic motion 11/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

19. The Physical Pendulum For small  (  < 10°): 11/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

23. TERIMA KASIH 11/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |