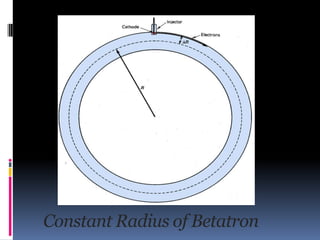
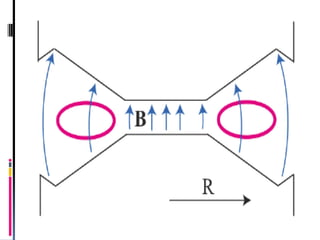
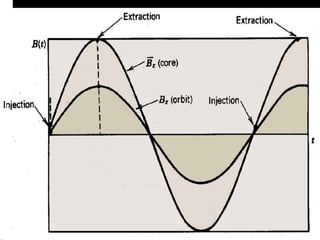
A betatron is a device that accelerates electrons using an expanding magnetic field within a doughnut-shaped vacuum chamber. Electrons are injected into the chamber and accelerated as the magnetic field strength increases over time. This increasing magnetic flux induces an electric field that increases the electrons' energy, allowing them to gain extremely high speeds. The betatron condition requires that the rate of change of magnetic flux through the circular orbit equals 2π times the radius squared times the rate of change of the magnetic field, in order to maintain the electrons' constant orbital radius as they accelerate.

2. BETATRON
Betatron is a device for speeding up electron to
extremely high energies with the help of expending
magnetic field.
It was constructed in 1941 by D.W.Kerst.

3. K.W. Kerst with BETATRON

4. Betatron Differs from cyclotron
The electrons are accelerated by expending magnetic field.
 The circular orbit has a constant radius.

5. Different Betatrons
According to their
Generations

8. Constant Radius of Betatron

9. Construction
Betatron consists of highly evacuated angular tube D known as
doughnut chamber.
The chamber is placed between the poles of an electromagnet
excited by an alternating current (frequency of 60 or 180 Hz)
Electrons are produced by electron gun and are injected into
doughnut at the beginning of each cycle of alternate current.
The increasing magnetic flux gives rise to a voltage
gradient(electric field) round the doughnut which accelerates the
orbiting electrons

11. PRINCIPLE
The principle of the betatron is the same as that of a transformer in which an
Alternating current applied to the primary coil induces an alternating current
In the secondary.
In betatron secondary coil is replaced by a doughnut shaped vaccum chamber.
When the electron is injected in doughnut, the alternating magnetic field has
two effects :
 An electromotive force is produced in the electron orbit by changing
magnetic flux that gives an additional energy to the electrons.
 A radial force is produced by the reaction of magnetic field whose direction
is perpendicular to the electron velocity which keeps the electrons moving
in the circular part.

13. OPERATION
Electrons from the electron gun are injected into doughnut shaped
vacuum chamber when the magnetic field is just rising from its zero
value in the first quarter cycle.
The electrons now make several thousand revolution and gain energy.
When the magnetic field has reached its maximum value, the electrons
are pulled out from their orbit.
Either they strike a target and produce X-rays or emerge from the
apparatus through a window

15. BETATRON CONDITION
Consider an electron is moving in a circular orbit of radius ’r’ in the magnetic field.
Let at any instant, B be the magnetic field at this orbit and the total magnetic flux through
the orbit is ΦB. The flux ΦB increases at the rate of d/dt (ΦB) and the induced e.m.f. In
the orbit is given by
Induced e.m.f. = d /dt (ΦB) .....(i)
work done on the electron in one revolution
= induced e.m.f. X Charge
= - d/dt (ΦB) x e
Thus work done must be equal to the tangential force F acting on the electron
multiplied by the length of the orbit path i.e.,
work done = Force x Distance
=Fx2πr
Therefore, F x 2 π r = - d/dt (ΦB) x e
F =- e/ 2 π r x {d/dt (ΦB)} ....(ii)

16. The force F will increase the electron energy and which in turn would tend to
increase the orbit of large radius. In order to maintain the radius of the orbit,
The force experienced by the electron must be counteracted. Suppose the velocity
Of the electron is v and its mass is m. When the electron moves in an orbit of
Radius r under the action of field of magnetic induction B, the inward radial
force B e v is to be equal to the upwards centrifugal force mv2/r .
Therefore, B e v = m v2 / r
m v=Ber ....(iii)
According to Newton’s law, the force is defined at the rate of change of
momentum (p=m v) i.e.,
F = d/dt (B e r)
= er dB/dt ....(iv)

17. To maintain the radius constant, the value of F given in equation (ii) and
Equation (iv), should numerically, hence
e/ 2 π r x {d/dt (ΦB)} = e r dB/dt
d/dt (ΦB) = 2 π r2 dB/dt
Integrating, we get
ΦB = 2 π r2 B
This is known as Betatron condition