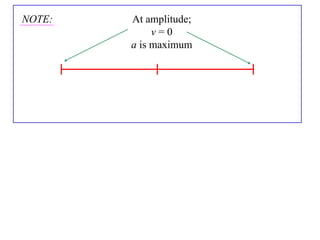
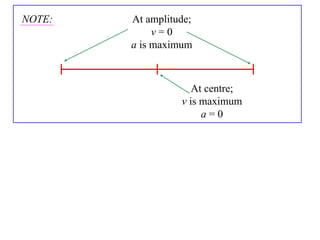
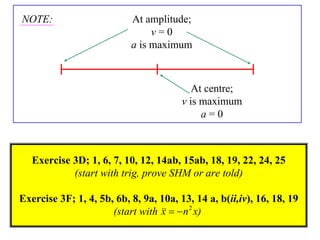
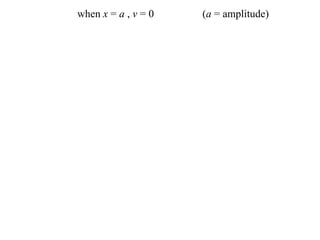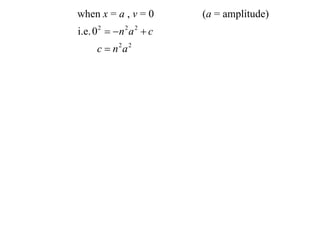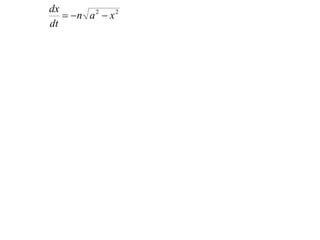A particle undergoes simple harmonic motion (SHM) if its acceleration is directly proportional to its displacement from a fixed point. For a particle undergoing SHM: - Its motion obeys the differential equation ä = -n2x - Its position is given by x = a cos(nt) or x = a sin(nt), where a is the amplitude - It oscillates periodically between -a and a - The period is T = 2π/n and the frequency is f = 1/T

1. Simple Harmonic Motion

2. Simple Harmonic Motion
A particle that moves back and forward in such a way that its
acceleration at any instant is directly proportional to its distance from
a fixed point, is said to undergo Simple Harmonic Motion (SHM)

3. Simple Harmonic Motion
A particle that moves back and forward in such a way that its
acceleration at any instant is directly proportional to its distance from
a fixed point, is said to undergo Simple Harmonic Motion (SHM)
 x
x

4. Simple Harmonic Motion
A particle that moves back and forward in such a way that its
acceleration at any instant is directly proportional to its distance from
a fixed point, is said to undergo Simple Harmonic Motion (SHM)
 x
x
  kx
x

5. Simple Harmonic Motion
A particle that moves back and forward in such a way that its
acceleration at any instant is directly proportional to its distance from
a fixed point, is said to undergo Simple Harmonic Motion (SHM)
 x
x
  kx
x
   n 2 x
x

6. Simple Harmonic Motion
A particle that moves back and forward in such a way that its
acceleration at any instant is directly proportional to its distance from
a fixed point, is said to undergo Simple Harmonic Motion (SHM)
 x
x
  kx
x
   n 2 x (constant needs to be negative)
x

7. Simple Harmonic Motion
A particle that moves back and forward in such a way that its
acceleration at any instant is directly proportional to its distance from
a fixed point, is said to undergo Simple Harmonic Motion (SHM)
 x
x
  kx
x
   n 2 x (constant needs to be negative)
x
If a particle undergoes SHM, then it obeys;
   n 2 x
x

8. Simple Harmonic Motion
A particle that moves back and forward in such a way that its
acceleration at any instant is directly proportional to its distance from
a fixed point, is said to undergo Simple Harmonic Motion (SHM)
 x
x
  kx
x
   n 2 x (constant needs to be negative)
x
If a particle undergoes SHM, then it obeys;
   n 2 x
x
d 1 2 
 v   n x
2
dx  2 

9. Simple Harmonic Motion
A particle that moves back and forward in such a way that its
acceleration at any instant is directly proportional to its distance from
a fixed point, is said to undergo Simple Harmonic Motion (SHM)
 x
x
  kx
x
   n 2 x (constant needs to be negative)
x
If a particle undergoes SHM, then it obeys;
   n 2 x
x
d 1 2 
 v   n x
2
dx  2 
1 2 1 2 2
v   n x c
2 2
v 2  n 2 x 2  c

10. when x = a , v = 0 (a = amplitude)

11. when x = a , v = 0 (a = amplitude)
i.e. 0 2   n 2 a 2  c
c  n2a 2

12. when x = a , v = 0 (a = amplitude)
i.e. 0 2   n 2 a 2  c
c  n2a 2
v 2  n 2 x 2  n 2 a 2
v 2  n 2 a 2  x 2 
v  n a 2  x 2

13. when x = a , v = 0 (a = amplitude)
i.e. 0 2   n 2 a 2  c
c  n2a 2
v 2  n 2 x 2  n 2 a 2
v 2  n 2 a 2  x 2 
v  n a 2  x 2
NOTE: v2  0

14. when x = a , v = 0 (a = amplitude)
i.e. 0 2   n 2 a 2  c
c  n2a 2
v 2  n 2 x 2  n 2 a 2
v 2  n 2 a 2  x 2 
v  n a 2  x 2
NOTE: v2  0
a2  x2  0

15. when x = a , v = 0 (a = amplitude)
i.e. 0 2   n 2 a 2  c
c  n2a 2
v 2  n 2 x 2  n 2 a 2
v 2  n 2 a 2  x 2 
v  n a 2  x 2
NOTE: v2  0
a2  x2  0
a  x  a

16. when x = a , v = 0 (a = amplitude)
i.e. 0 2   n 2 a 2  c
c  n2a 2
v 2  n 2 x 2  n 2 a 2
v 2  n 2 a 2  x 2 
v  n a 2  x 2
NOTE: v2  0
a2  x2  0
a  x  a
 Particle travels back and forward between x = -a and x = a

17. dx
 n a 2  x 2
dt

18. dx
 n a 2  x 2
dt If when t  0;
x   a, choose - ve and cos -1
x  0, choose  ve and sin -1

19. dx
 n a 2  x 2
dt If when t  0;
dt 1 x   a, choose - ve and cos -1

dx n a 2  x 2
x  0, choose  ve and sin -1

20. dx
 n a 2  x 2
dt If when t  0;
dt 1 x   a, choose - ve and cos -1

dx n a 2  x 2
x  0, choose  ve and sin -1
1
x
1
t  2 dx
na a x 2

21. dx
 n a 2  x 2
dt If when t  0;
dt 1 x   a, choose - ve and cos -1

dx n a 2  x 2
x  0, choose  ve and sin -1
1
x
1
t  2 dx
na a x 2
x
1  1 x 
 cos 
n aa

22. dx
 n a 2  x 2
dt If when t  0;
dt 1 x   a, choose - ve and cos -1

dx n a 2  x 2
x  0, choose  ve and sin -1
1
x
1
t  2 dx
na a x 2
x
1  1 x 
 cos 
n aa
1  1 x 
 cos  cos 1 1
n a 
1 1 x
 cos
n a

23. dx
 n a 2  x 2
dt If when t  0;
dt 1 x   a, choose - ve and cos -1

dx n a 2  x 2
x  0, choose  ve and sin -1
1
x
1
t  2 dx
na a x 2
x
1  1 x 
 cos 
n aa
1  1 x 
 cos  cos 1 1
n a 
1 x
 cos 1
n a
1 x
nt  cos
a
x
 cos nt
a
x  a cos nt

24. In general;

25. In general;
A particle undergoing SHM obeys
   n 2 x
x

26. In general;
A particle undergoing SHM obeys
   n 2 x
x
v 2  n 2 a 2  x 2 

27. In general;
A particle undergoing SHM obeys
   n 2 x
x
v 2  n 2 a 2  x 2   allows us to find path of the particle

28. In general;
A particle undergoing SHM obeys
   n 2 x
x
v 2  n 2 a 2  x 2   allows us to find path of the particle
x  a cos nt

29. In general;
A particle undergoing SHM obeys
   n 2 x
x
v 2  n 2 a 2  x 2   allows us to find path of the particle
x  a cos nt OR x  a sin nt
where a  amplitude

30. In general;
A particle undergoing SHM obeys
   n 2 x
x
v 2  n 2 a 2  x 2   allows us to find path of the particle
x  a cos nt OR x  a sin nt
where a  amplitude
the particle has;

31. In general;
A particle undergoing SHM obeys
   n 2 x
x
v 2  n 2 a 2  x 2   allows us to find path of the particle
x  a cos nt OR x  a sin nt
where a  amplitude
the particle has;
2
period : T 
n
1
frequency : f 
T

32. In general;
A particle undergoing SHM obeys
   n 2 x
x
v 2  n 2 a 2  x 2   allows us to find path of the particle
x  a cos nt OR x  a sin nt
where a  amplitude
the particle has;
2
period : T  (time for one oscillation)
n
1
frequency : f 
T

33. In general;
A particle undergoing SHM obeys
   n 2 x
x
v 2  n 2 a 2  x 2   allows us to find path of the particle
x  a cos nt OR x  a sin nt
where a  amplitude
the particle has;
2
period : T  (time for one oscillation)
n
1
frequency : f  (number of oscillations
T per time period)

34. e.g. (i) A particle, P, moves on the x axis according to the law x = 4sin3t.

35. e.g. (i) A particle, P, moves on the x axis according to the law x = 4sin3t.
a) Show that P is moving in SHM and state the period of motion.

36. e.g. (i) A particle, P, moves on the x axis according to the law x = 4sin3t.
a) Show that P is moving in SHM and state the period of motion.
x  4 sin 3t
x  12 cos 3t

  36 sin 3t
x

37. e.g. (i) A particle, P, moves on the x axis according to the law x = 4sin3t.
a) Show that P is moving in SHM and state the period of motion.
x  4 sin 3t
x  12 cos 3t

  36 sin 3t
x
 9 x

38. e.g. (i) A particle, P, moves on the x axis according to the law x = 4sin3t.
a) Show that P is moving in SHM and state the period of motion.
x  4 sin 3t
x  12 cos 3t

  36 sin 3t
x
 9 x
 particle moves in SHM

39. e.g. (i) A particle, P, moves on the x axis according to the law x = 4sin3t.
a) Show that P is moving in SHM and state the period of motion.
x  4 sin 3t
x  12 cos 3t

  36 sin 3t
x
 9 x
 particle moves in SHM
2
T
3

40. e.g. (i) A particle, P, moves on the x axis according to the law x = 4sin3t.
a) Show that P is moving in SHM and state the period of motion.
x  4 sin 3t
x  12 cos 3t

  36 sin 3t
x
 9 x
 particle moves in SHM
2
T
3
2
 period of motion is seconds
3

41. e.g. (i) A particle, P, moves on the x axis according to the law x = 4sin3t.
a) Show that P is moving in SHM and state the period of motion.
x  4 sin 3t
x  12 cos 3t

  36 sin 3t
x
 9 x
 particle moves in SHM
2
T
3
2
 period of motion is seconds
3
b) Find the interval in which the particle moves and determine the
greatest speed.

42. e.g. (i) A particle, P, moves on the x axis according to the law x = 4sin3t.
a) Show that P is moving in SHM and state the period of motion.
x  4 sin 3t
x  12 cos 3t

  36 sin 3t
x
 9 x
 particle moves in SHM
2
T
3
2
 period of motion is seconds
3
b) Find the interval in which the particle moves and determine the
greatest speed.
 particle moves along the interval  4  x  4
and the greatest speed is 12 units/s

43. (ii) A particle moves so that its acceleration is given by   4 x
x
Initially the particle is 3cm to the right of O and traveling with a
velocity of 6cm/s.
Find the interval in which the particle moves and determine the
greatest acceleration.

44. (ii) A particle moves so that its acceleration is given by   4 x
x
Initially the particle is 3cm to the right of O and traveling with a
velocity of 6cm/s.
Find the interval in which the particle moves and determine the
greatest acceleration.
d 1 2 
 v   4 x
dx  2 

45. (ii) A particle moves so that its acceleration is given by   4 x
x
Initially the particle is 3cm to the right of O and traveling with a
velocity of 6cm/s.
Find the interval in which the particle moves and determine the
greatest acceleration.
d 1 2 
 v   4 x
dx  2 
1 2
v  2 x 2  c
2
v 2  4 x 2  c

46. (ii) A particle moves so that its acceleration is given by   4 x
x
Initially the particle is 3cm to the right of O and traveling with a
velocity of 6cm/s.
Find the interval in which the particle moves and determine the
greatest acceleration.
d 1 2 
 v   4 x
dx  2 
1 2
v  2 x 2  c
2
v 2  4 x 2  c
when x  3, v  6
i.e. 6 2  43  c
2
c  72

47. (ii) A particle moves so that its acceleration is given by   4 x
x
Initially the particle is 3cm to the right of O and traveling with a
velocity of 6cm/s.
Find the interval in which the particle moves and determine the
greatest acceleration.
d 1 2 
 v   4 x
dx  2 
1 2
v  2 x 2  c
2
v 2  4 x 2  c
when x  3, v  6
i.e. 6 2  43  c
2
c  72
v 2  4 x 2  72

48. (ii) A particle moves so that its acceleration is given by   4 x
x
Initially the particle is 3cm to the right of O and traveling with a
velocity of 6cm/s.
Find the interval in which the particle moves and determine the
greatest acceleration.
d 1 2  But v 2  0
 v   4 x
dx  2   4 x 2  72  0
1 2 x 2  18
v  2 x 2  c
2
3 2  x  3 2
v 2  4 x 2  c
when x  3, v  6
i.e. 6 2  43  c
2
c  72
v 2  4 x 2  72

49. (ii) A particle moves so that its acceleration is given by   4 x
x
Initially the particle is 3cm to the right of O and traveling with a
velocity of 6cm/s.
Find the interval in which the particle moves and determine the
greatest acceleration.
d 1 2  But v 2  0
 v   4 x
dx  2   4 x 2  72  0
1 2 x 2  18
v  2 x 2  c
2
3 2  x  3 2
v 2  4 x 2  c
when x  3, v  6 when x  3 2,   43 2 
x
i.e. 6 2  43  c
2  12 2
c  72
v 2  4 x 2  72

50. (ii) A particle moves so that its acceleration is given by   4 x
x
Initially the particle is 3cm to the right of O and traveling with a
velocity of 6cm/s.
Find the interval in which the particle moves and determine the
greatest acceleration.
d 1 2  But v 2  0
 v   4 x
dx  2   4 x 2  72  0
1 2 x 2  18
v  2 x 2  c
2
3 2  x  3 2
v 2  4 x 2  c
when x  3, v  6 when x  3 2,   43 2 
x
i.e. 6 2  43  c
2  12 2
c  72  greatest acceleration is 12 2 cm/s 2
v 2  4 x 2  72

51. NOTE:

52. NOTE: At amplitude;
v=0
a is maximum

53. NOTE: At amplitude;
v=0
a is maximum
At centre;
v is maximum
a=0

54. NOTE: At amplitude;
v=0
a is maximum
At centre;
v is maximum
a=0
Exercise 3D; 1, 6, 7, 10, 12, 14ab, 15ab, 18, 19, 22, 24, 25
(start with trig, prove SHM or are told)
Exercise 3F; 1, 4, 5b, 6b, 8, 9a, 10a, 13, 14 a, b(ii,iv), 16, 18, 19
(start with    n 2 x)
x