This document discusses two degree of freedom systems and provides equations of motion for a two degree of freedom spring-mass system with damping. It presents the matrix form of the equations of motion and defines the mass, damping and stiffness matrices. It then analyzes the free vibration of an undamped two degree of freedom system, determining the natural frequencies and normal modes of vibration. The normal modes allow expressing the motion as a superposition of the individual mode shapes.

1. GANDHINAGAR INSTITUTE
OF TECHNOLOGY
Subject: Dynamics of machine
Topic:-Two degree of freedom system
Branch:-Mechanical
Sem.:-6
Div:-D
Prepared By:- Guided By:-
Patel Yash S. (150123119039) Prof. Samir Raval

2. INTRODUCTION
• The System which require two independent
co-ordinates to specify its motion at
configuration at instant is called two degree of
freedom system.
– Example: motor pump system.
• There are two equations of motion for a 2DOF
system, one for each mass (more precisely, for
each DOF).
• They are generally in the form of couple
differential equation that is, each equation
involves all the coordinates.

3. Equation of motion for forced vibration
• Consider a viscously damped two degree of freedom
spring-mass system, shown in Fig.
Figure. A two degree of freedom spring-mass-damper system

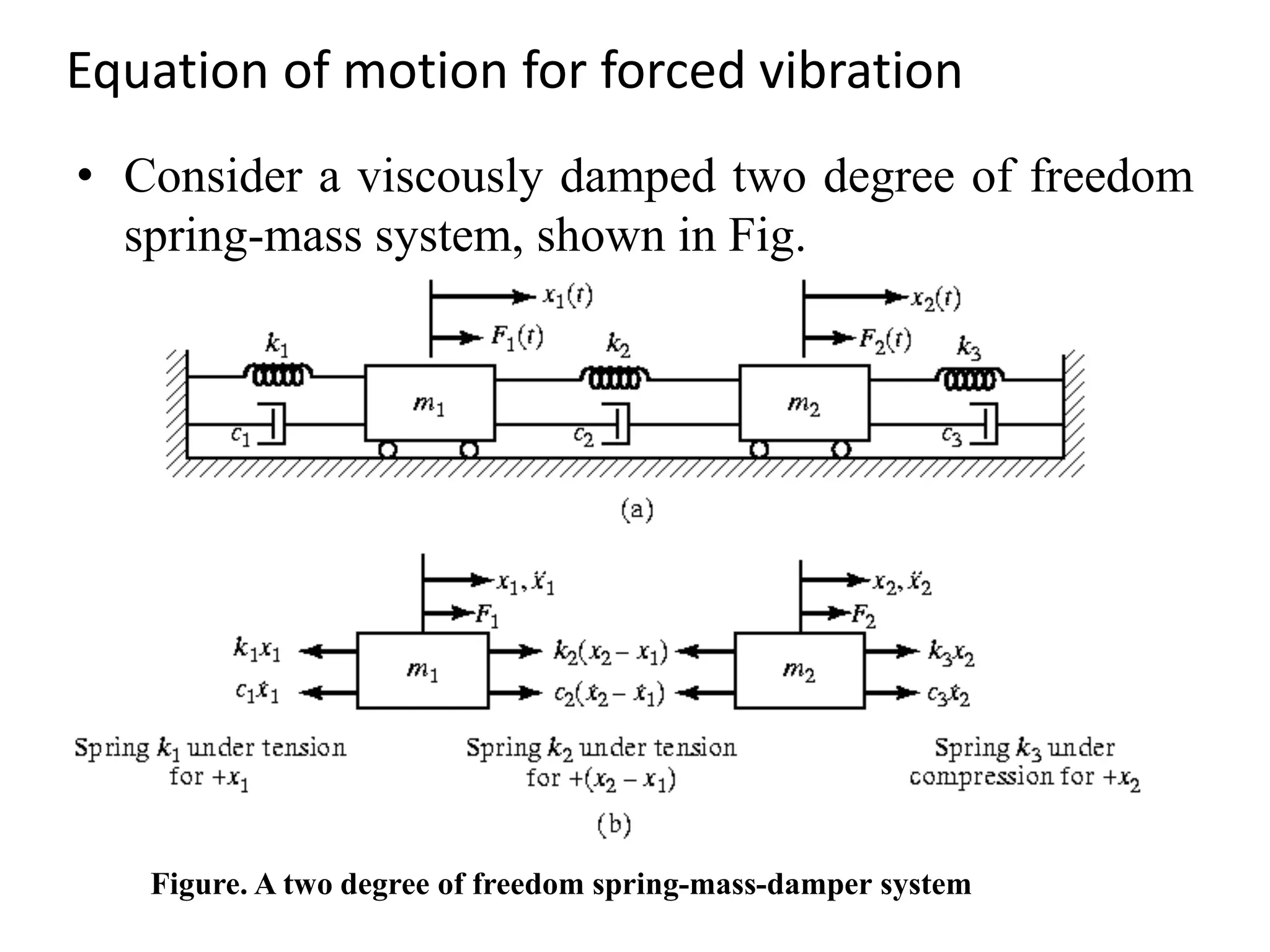
4. Equations of Motion for Forced Vibration
)2.5()()(
)1.5()()(
2232122321222
1221212212111
Fxkkxkxccxcxm
Fxkxkkxcxccxm




)3.5()()(][)(][)(][ tFtxktxctxm


Both equations can be written in matrix form as
The application of Newton’s second law of motion to each
of the masses gives the equations of motion:
where [m], [c], and [k] are called the mass, damping,
and stiffness matrices, respectively, and are given by

5. Equations of Motion for Forced Vibration
























322
221
322
221
2
1
][
][
0
0
][
kkk
kkk
k
ccc
ccc
c
m
m
m














)(
)(
)(
)(
)(
)(
2
1
2
1
tF
tF
tF
tx
tx
tx

And the displacement and force vectors are given
respectively:
It can be seen that the matrices [m], [c], and [k] are all 2 x
2 matrices whose elements are known masses, damping
coefficient and stiffnesses of the system, respectively.

6. Equations of Motion for Forced Vibration
][][],[][],[][ kkccmm TTT

6
where the superscript T denotes the transpose of the
matrix.
oThe solution of Eqs.(5.1) and (5.2) involves four
constants of integration (two for each equation). Usually
the initial displacements and velocities of the two masses
are specified as
oFurther, these matrices can be seen to be symmetric,
so that,
x1(t = 0) = x1(0) and 1( t = 0) = 1(0),
x2(t = 0) = x2(0) and 2 (t = 0) = 2(0).
x
x x
x

7. Free Vibration Analysis of an Undamped System
)5.5(0)()()()(
)4.5(0)()()()(
2321222
2212111


txkktxktxm
txktxkktxm


)6.5()cos()(
)cos()(
22
11




tXtx
tXtx
7
Assuming that it is possible to have harmonic motion of
m1 and m2 at the same frequency ω and the same phase
angle Φ, we take the solutions as
By setting F1(t) = F2(t) = 0, and damping disregarded, i.e.,
c1 = c2 = c3 = 0, and the equation of motion is reduced to:

8. Free Vibration Analysis of an Undamped System
  
   )7.5(0)cos()(
0)cos()(
232
2
212
22121
2
1




tXkkmXk
tXkXkkm
 
  )8.5(0)(
0)(
232
2
212
22121
2
1


XkkmXk
XkXkkm


Since Eq.(5.7)must be satisfied for all values of the time t,
the terms between brackets must be zero. Thus,
Substituting into Eqs.(5.4) and (5.5),

9. Free Vibration Analysis of an Undamped System
 
 
0
)(
)(
det
21
2
12
221
2
1











kkmk
kkkm


 
  )9.5(0))((
)()()(
2
23221
132221
4
21


kkkkk
mkkmkkmm 
or
which represent two simultaneous homogenous algebraic
equations in the unknown X1 and X2. For trivial solution,
i.e., X1 = X2 = 0, there is no solution. For a nontrivial
solution, the determinant of the coefficients of X1 and X2
must be zero:

10. )10.5(
))((
4
)()(
2
1
)()(
2
1
,
2/1
21
2
23221
2
21
132221
21
1322212
2
2
1





 










 





 

mm
kkkkk
mm
mkkmkk
mm
mkkmkk


The roots are called natural frequencies of the system.
which is called the frequency or characteristic equation.
Hence the roots are:
FREE VIBRATION ANALYSIS OF AN UNDAMPED SYSTEM

11. Free Vibration Analysis of an Undamped System
)11.5(
)(
)(
)(
)(
32
2
22
2
2
21
2
21
)2(
1
)2(
2
2
32
2
12
2
2
21
2
11
)1(
1
)1(
2
1
kkm
k
k
kkm
X
X
r
kkm
k
k
kkm
X
X
r












)12.5(and )2(
12
)2(
1
)2(
2
)2(
1)2(
)1(
11
)1(
1
)1(
2
)1(
1)1(




































Xr
X
X
X
X
Xr
X
X
X
X

The normal modes of vibration corresponding to ω1
2
and ω2
2 can be expressed, respectively, as
To determine the values of X1 and X2, given ratio
which are known as the modal vectors of the system.

12. Free Vibration Analysis of an Undamped System
(5.17)modesecond
)cos(
)cos(
)(
)(
)(
modefirst
)cos(
)cos(
)(
)(
)(
22
)2(
12
22
)2(
1
)2(
2
)2(
1)2(
11
)1(
11
11
)1(
1
)1(
2
)1(
1)1(














































tXr
tX
tx
tx
tx
tXr
tX
tx
tx
tx


0)0(,)0(
,0)0(constant,some)0(
2
)(
12
1
)(
11


txXrtx
txXtx
i
i
i


Where the constants , , and are determined by
the initial conditions. The initial conditions are
The free vibration solution or the motion in time can be
expressed itself as
)1(
1X )2(
1X 1 2

13. Free Vibration Analysis of an Undamped System
)14.5()()()( 2211 txctxctx


)15.5()cos()cos(
)()()(
)cos()cos()()()(
22
)2(
1211
)1(
11
)2(
2
)1(
22
22
)2(
111
)1(
1
)2(
1
)1(
11





tXrtXr
txtxtx
tXtXtxtxtx
Thus the components of the vector can be expressed as
The resulting motion can be obtained by a linear
superposition of the two normal modes, Eq.(5.13)
where the unknown constants can be determined from
the initial conditions:

14. Free Vibration Analysis of an Undamped System
)16.5()0()0(),0()0(
),0()0(),0()0(
2222
1111
xtxxtx
xtxxtx




)17.5(sinsin)0(
coscos)0(
sinsin)0(
coscos)0(
2
)2(
1221
)1(
1112
2
)2(
121
)1(
112
2
)2(
121
)1(
111
2
)2(
11
)1(
11




XrXrx
XrXrx
XXx
XXx










































)(
)0()0(
sin,
)(
)0()0(
sin
)0()0(
cos,
)0()0(
cos
122
211
2
)2(
1
121
212
1
)1(
1
12
211
2
)2(
1
12
212
1
)1(
1
rr
xxr
X
rr
xxr
X
rr
xxr
X
rr
xxr
X






Substituting into Eq.(5.15) leads to
The solution can be expressed as

15. Free Vibration Analysis of an Undamped System
    
   
    
   
)18.5(
)0()0([
)0()0(
tan
cos
sin
tan
)0()0([
)0()0(
tan
cos
sin
tan
)0()0(
)0()0(
)(
1
sincos
)0()0(
)0()0(
)(
1
sincos
2112
2111
2
)2(
1
2
)2(
11
2
2121
2121
1
)1(
1
1
)1(
11
1
2/1
2
2
2
2112
211
12
2/12
2
)2(
1
2
2
)2(
1
)2(
1
2/1
2
1
2
2122
212
12
2/12
1
)1(
1
2
1
)1(
1
)1(
1





































 









 






xxr
xxr
X
X
xxr
xxr
X
X
xxr
xxr
rr
XXX
xxr
xxr
rr
XXX














from which we obtain the desired solution

16. Example :Free Vibration Response of a Two Degree of
Freedom System
).0()0()0(,1)0( 2211 xxxx  
(E.1)
0
0
55-
53510
0
0
2
1
2
2
2
1
32
2
22
221
2
1














































X
X
X
X
kkmk
kkkm




Solution: For the given data, the eigenvalue
problem, Eq.(5.8), becomes
Find the free vibration response of the system shown in
Fig.5.3(a) with k1 = 30, k2 = 5, k3 = 0, m1 = 10, m2 = 1 and c1
= c2 = c3 = 0 for the initial conditions
or

17. Solution
(E.2)01508510 24
 
E.3)(4495.2,5811.1
0.6,5.2
21
2
2
2
1




E.5)(
5
1
E.4)(
2
1
)2(
1)2(
2
)2(
1)2(
)1(
1)1(
2
)1(
1)1(
X
X
X
X
X
X
X
X



































from which the natural frequencies can be found as
By setting the determinant of the coefficient matrix in
Eq.(E.1) to zero, we obtain the frequency equation,
The normal modes (or eigenvectors) are given by

18. Solution
(E.7))4495.2cos(5)5811.1cos(2)(
(E.6))4495.2cos()5811.1cos()(
2
)2(
11
)1(
12
2
)2(
11
)1(
11




tXtXtx
tXtXtx
(E.11)sin2475.121622.3)0(
(E.10)sin4495.2sin5811.10)0(
(E.9)cos5cos20)0(
(E.8)coscos1)0(
2
)2(
1
)1(
12
2
)2(
11
)1(
11
2
)2(
11
)1(
12
2
)2(
11
)1(
11




XXtx
XXtx
XXtx
XXtx






By using the given initial conditions in Eqs.(E.6) and
(E.7), we obtain
The free vibration responses of the masses m1 and m2
are given by (see Eq.5.15):

19. Solution
(E.12)
7
2
cos;
7
5
cos 2
)2(
11
)1(
1   XX
(E.13)0sin,0sin 2
)2(
11
)1(
1   XX
(E.14)0,0,
7
2
,
7
5
21
)2(
1
)1(
1  XX
while the solution of Eqs.(E.10) and (E.11) leads to
The solution of Eqs.(E.8) and (E.9) yields
Equations (E.12) and (E.13) give

20. Solution
(E.16)4495.2cos
7
10
5811.1cos
7
10
)(
(E.15)4495.2cos
7
2
5811.1cos
7
5
)(
2
1
tttx
tttx


Thus the free vibration responses of m1 and m2 are
given by

21. Torsional System
Figure : Torsional system with discs mounted on a shaft
Consider a torsional system as shown in Fig. The
differential equations of rotational motion for the discs
can be derived as

22. Torsional System
22312222
11221111
)(
)(
ttt
ttt
MkkJ
MkkJ






)19.5()(
)(
22321222
12212111
tttt
tttt
MkkkJ
MkkkJ






which upon rearrangement become
For the free vibration analysis of the system, Eq.(5.19)
reduces to
)20.5(0)(
0)(
2321222
2212111




ttt
ttt
kkkJ
kkkJ



23. Coordinate Coupling and Principal Coordinates
Generalized coordinates are sets of n coordinates used
to describe the configuration of the system.
•Equations of motion Using x(t) and θ(t).

24. Coordinate Coupling and Principal Coordinates
)21.5()()( 2211  lxklxkxm 
)22.5()()( 2221110 llxkllxkJ  
and the moment equation about C.G. can be expressed
as
From the free-body diagram shown in Fig.5.10a, with
the positive values of the motion variables as indicated,
the force equilibrium equation in the vertical direction
can be written as
Eqs.(5.21) and (5.22) can be rearranged and written in
matrix form as

25. Coordinate Coupling and Principal Coordinates
)23.5(
0
0
)()(
)()(
0
0
2
2
2
12211
221121
0 21 




































x
lklklklk
lklkkkx
J
m


  melyklykym  )()( 2211
The lathe rotates in the vertical plane and has vertical
motion as well, unless k1l1 = k2l2. This is known as
elastic or static coupling.
From Fig.5.10b, the equations of motion for translation
and rotation can be written as
•Equations of motion Using y(t) and θ(t).

26. Coordinate Coupling and Principal Coordinates
)24.5()()( 222111 ymellykllykJP
  
)25.5(
0
0
)()(
)()(
2
2
2
112211
112221
2 




































y
lklklklk
lklkkky
Jme
mem
P


2211 lklk 
These equations can be rearranged and written in
matrix form as
If , the system will have dynamic or inertia
coupling only.
Note the following characteristics of these systems:

27. Coordinate Coupling and Principal Coordinates
)26.5(
0
0
2
1
2221
1211
2
1
2221
1211
2
1
2221
1211













































x
x
kk
kk
x
x
cc
cc
x
x
mm
mm




1. In the most general case, a viscously damped two
degree of freedom system has the equations of
motions in the form:
2. The system vibrates in its own natural way regardless
of the coordinates used. The choice of the coordinates
is a mere convenience.
3. Principal or natural coordinates are defined as system
of coordinates which give equations of motion that are
uncoupled both statically and dynamically.

28. Example :Principal Coordinates of Spring-Mass System
Determine the principal coordinates for the spring-mass
system shown in Fig.

29. Solution
(E.1)
3
coscos)(
3
coscos)(
22112
22111




































t
m
k
Bt
m
k
Btx
t
m
k
Bt
m
k
Btx
We define a new set of coordinates such that
Approach: Define two independent solutions as principal
coordinates and express them in terms of the solutions
x1(t) and x2(t).
The general motion of the system shown is

30. Solution
(E.2)
3
cos)(
cos)(
222
111




















t
m
k
Btq
t
m
k
Btq
(E.3)0
3
0
22
11














q
m
k
q
q
m
k
q


Since the coordinates are harmonic functions, their
corresponding equations of motion can be written as

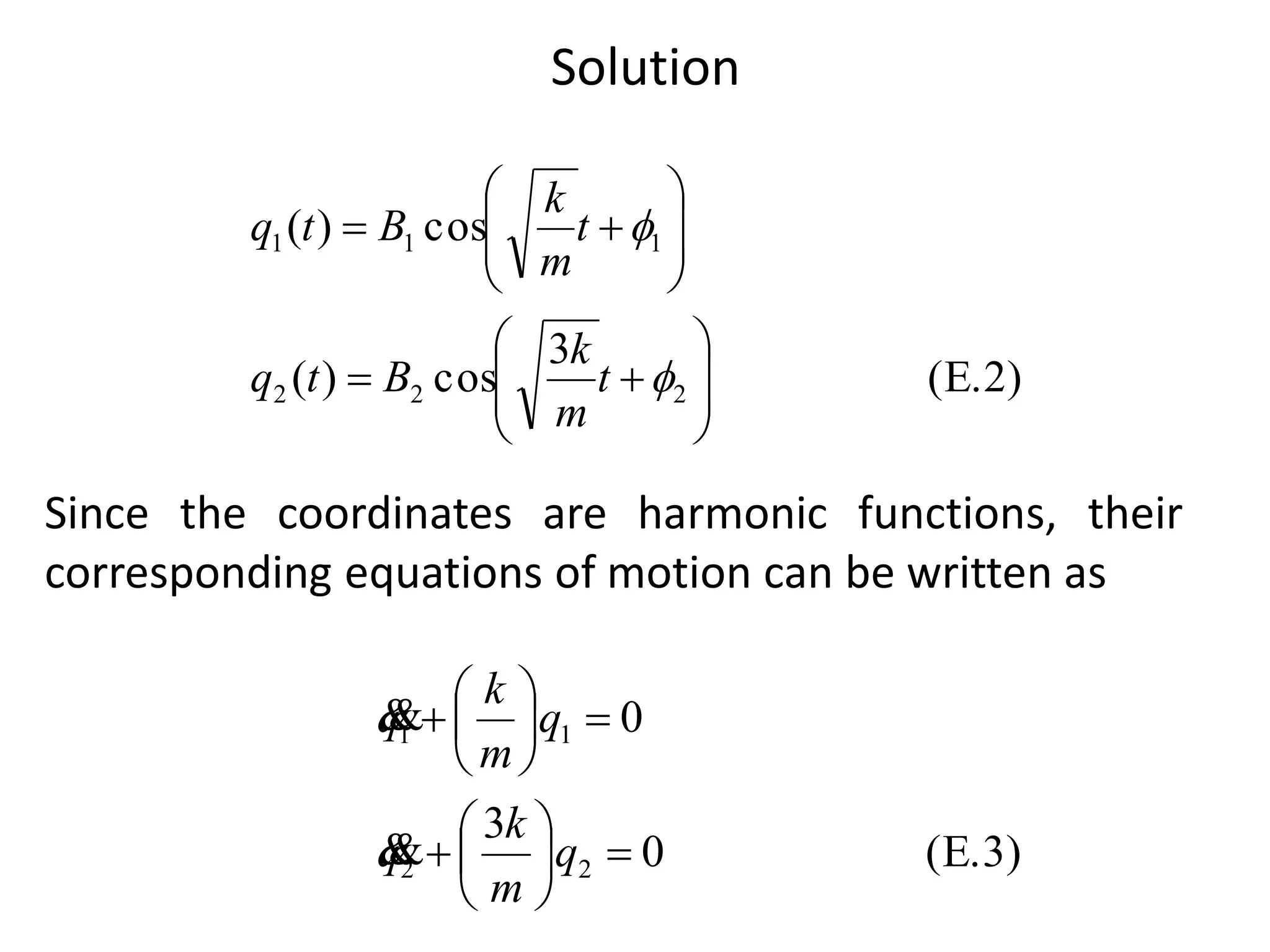
31. Solution
(E.4))()()(
)()()(
212
211
tqtqtx
tqtqtx


(E.5))]()([
2
1
)(
)]()([
2
1
)(
212
211
txtxtq
txtxtq


The solution of Eqs.(E.4) gives the principal coordinates:
From Eqs.(E.1) and (E.2), we can write

32. THANK YOU