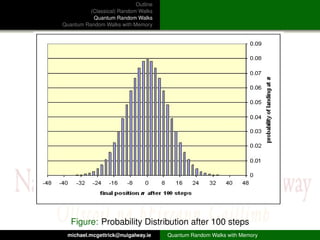
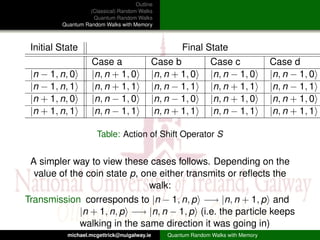
This document outlines and compares classical random walks, quantum random walks, and quantum random walks with memory. It introduces the key concepts of classical random walks on a line involving coin flips to move left or right. Quantum random walks are then described as taking place on a state space involving position and coin states, with transitions defined by unitary operators. Finally, quantum random walks with memory are discussed as generalizing the model to include memory of previous coin states.