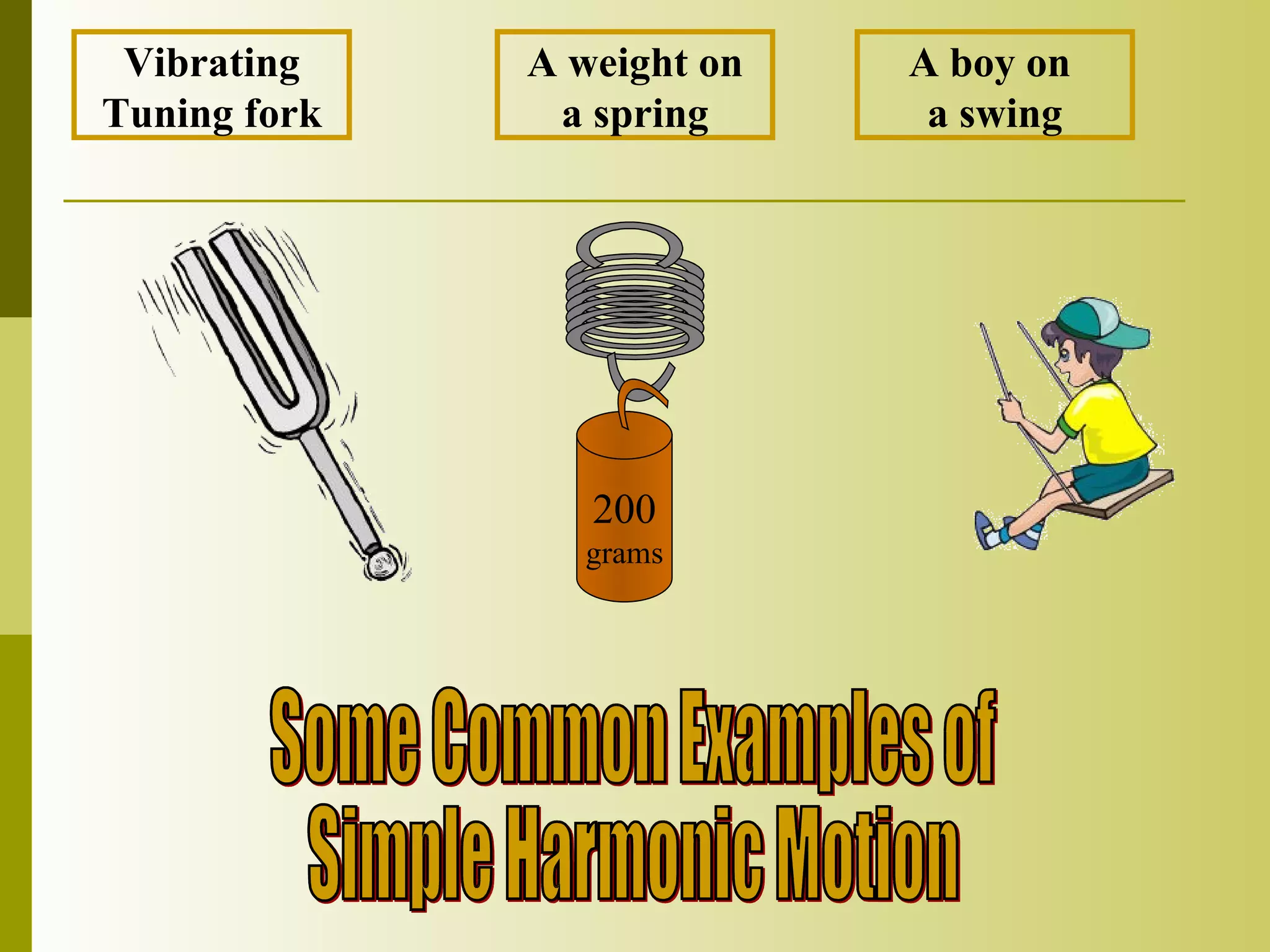
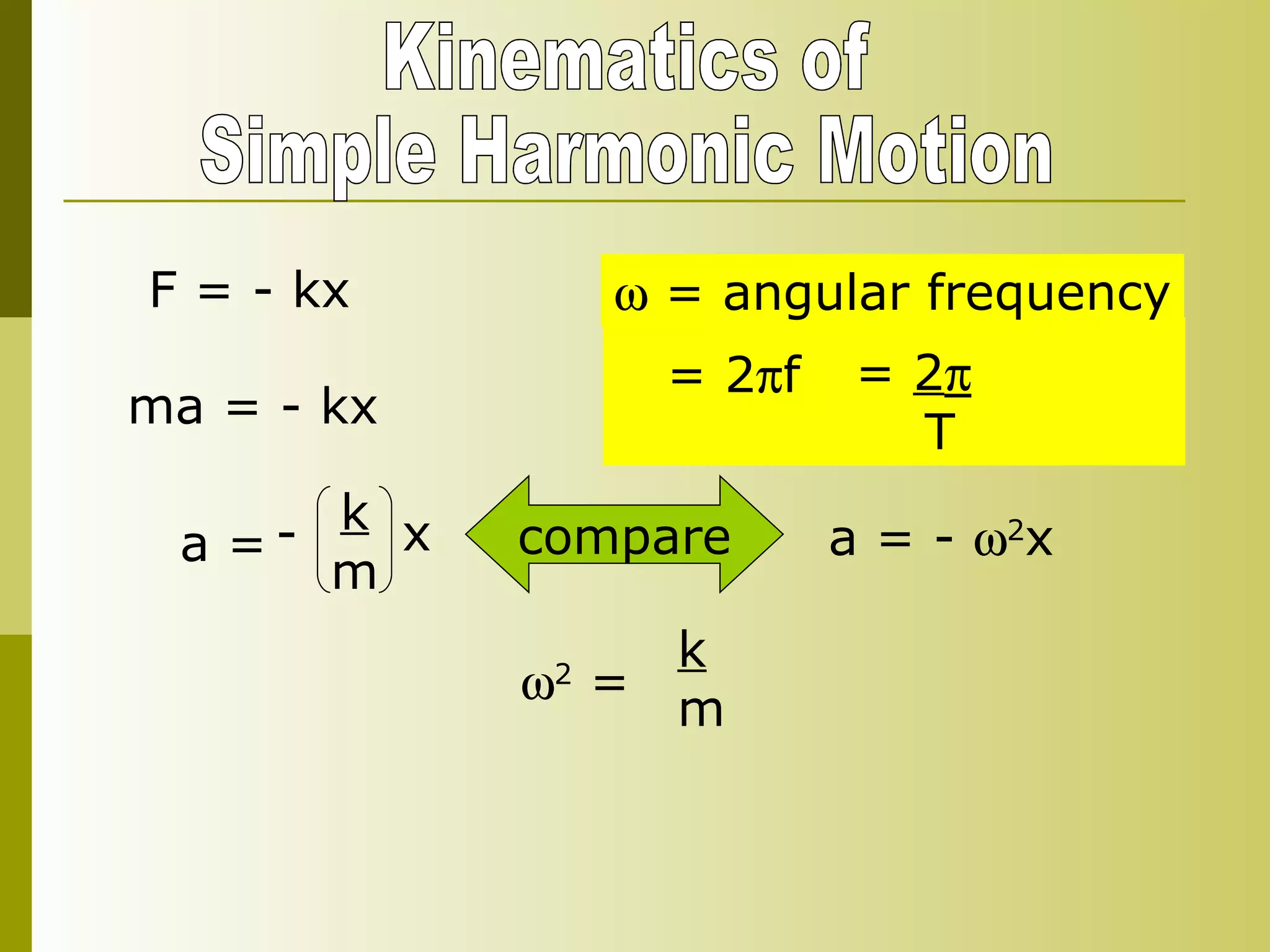
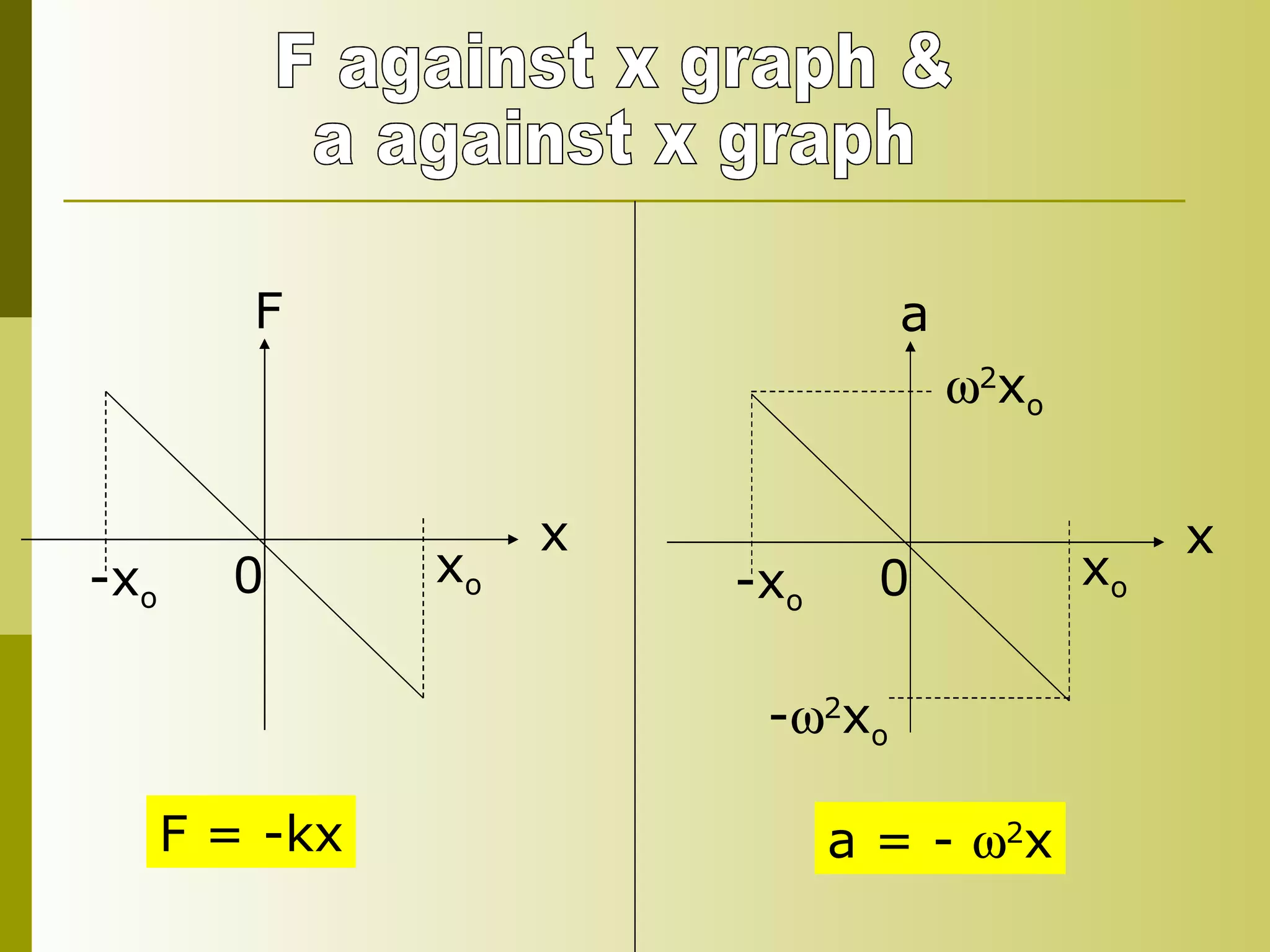
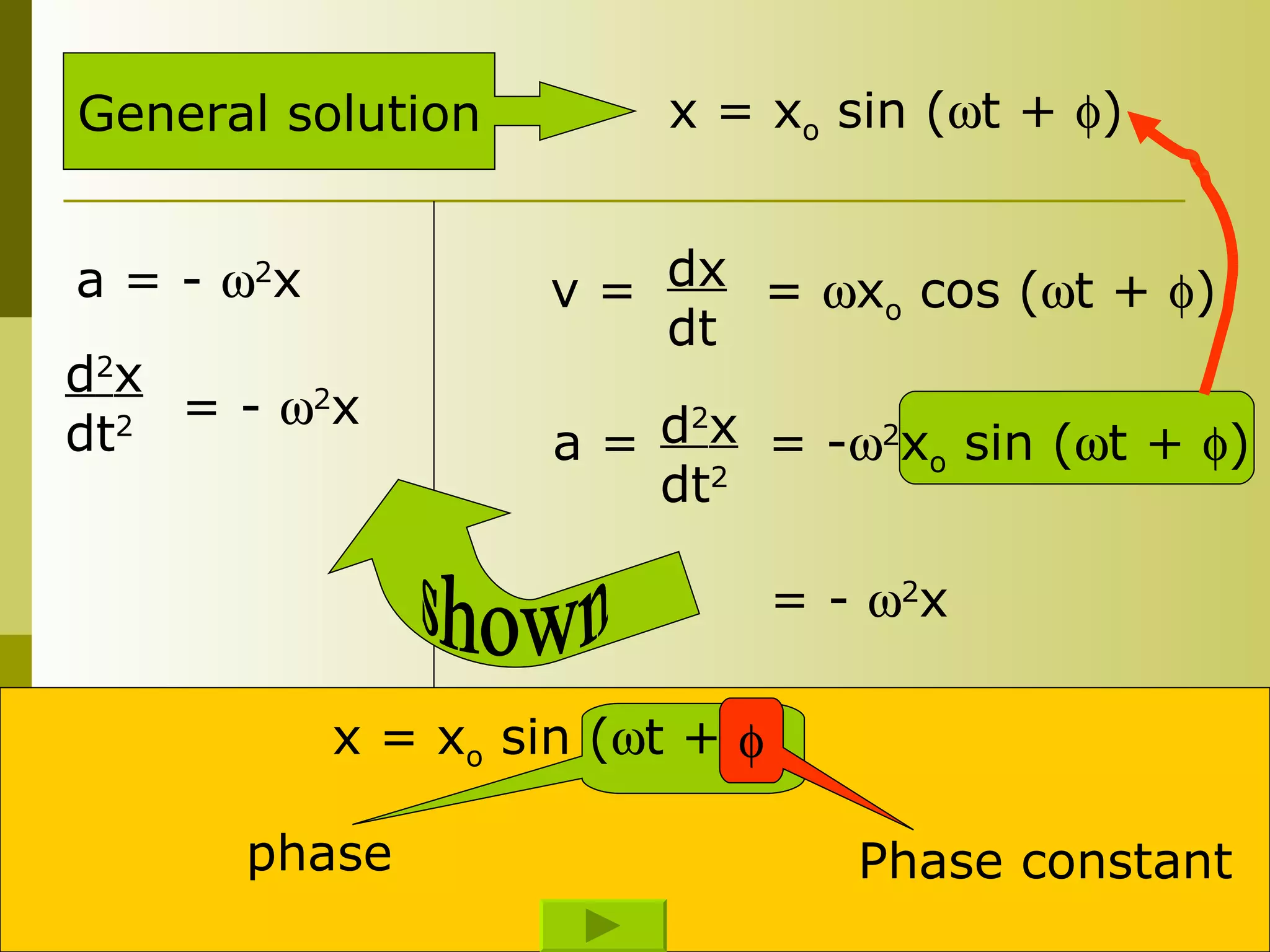
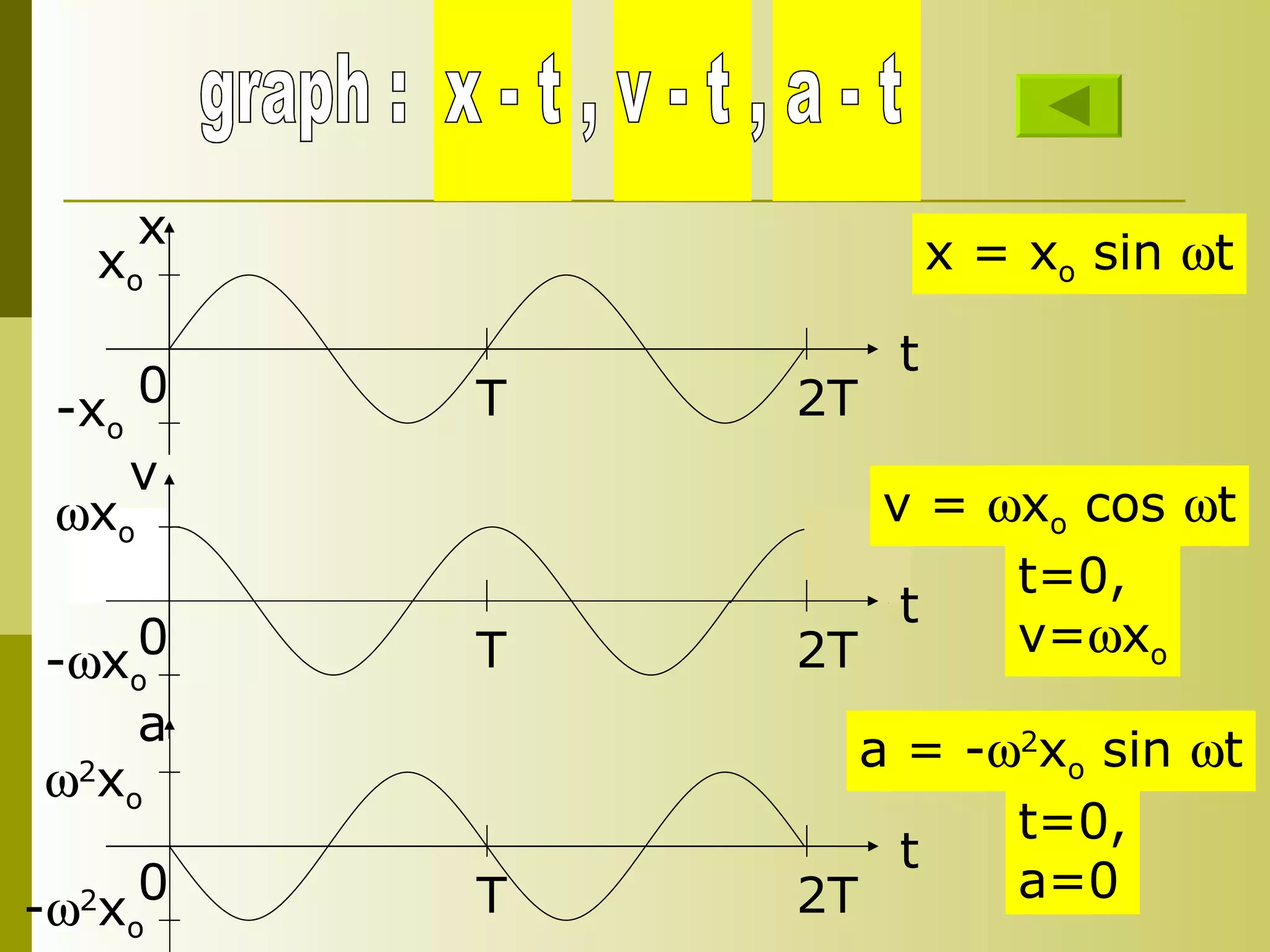
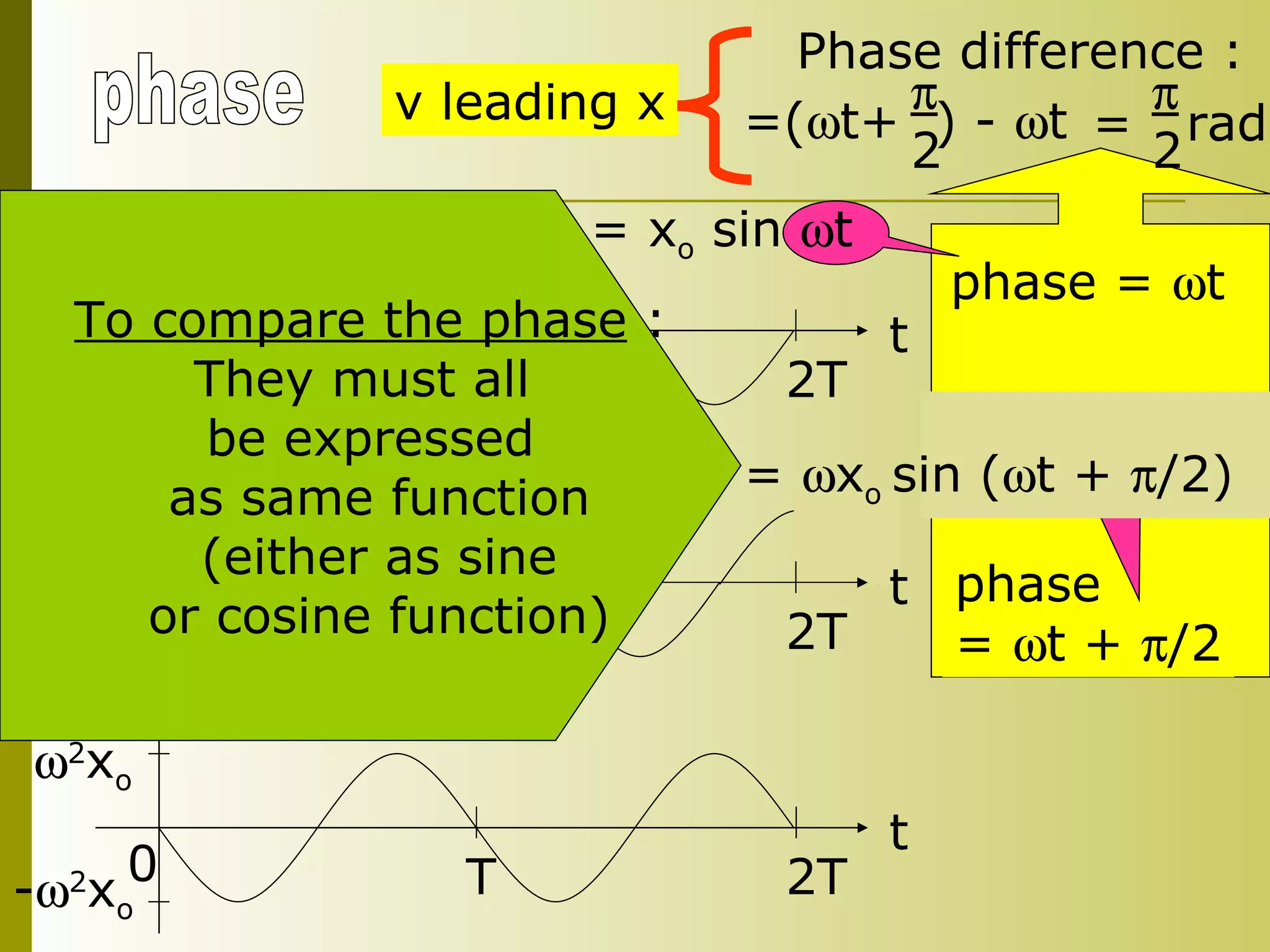
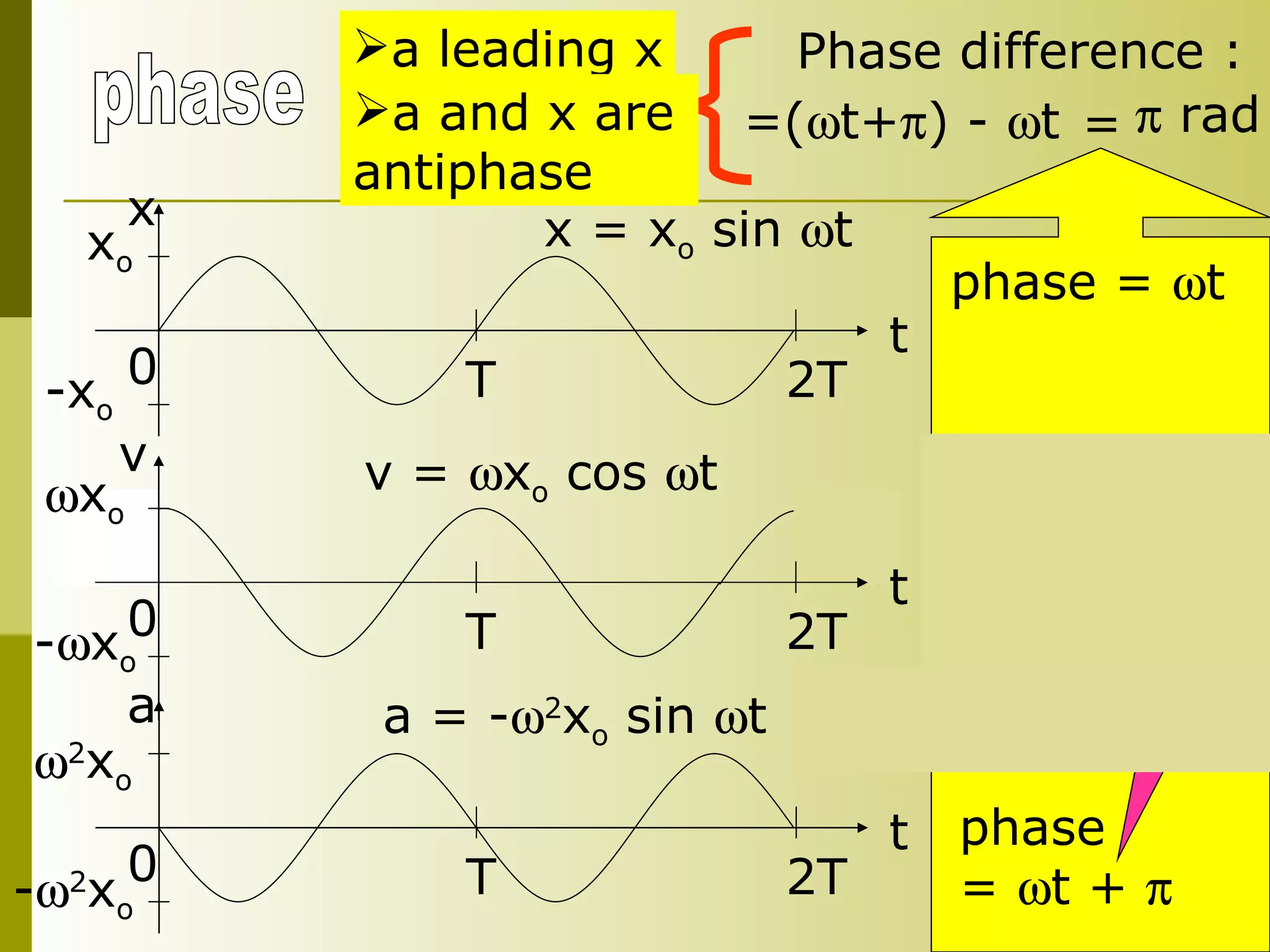
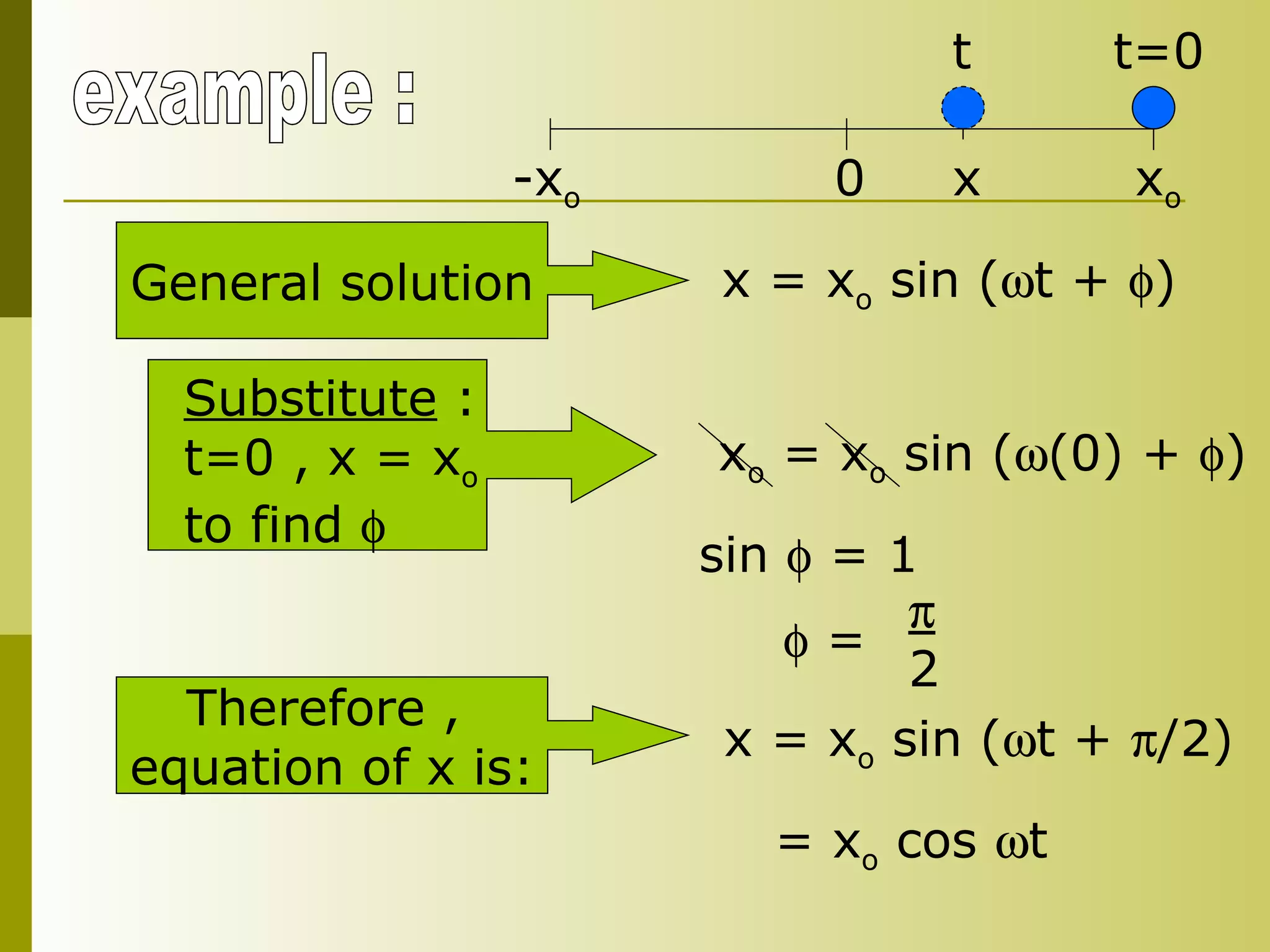
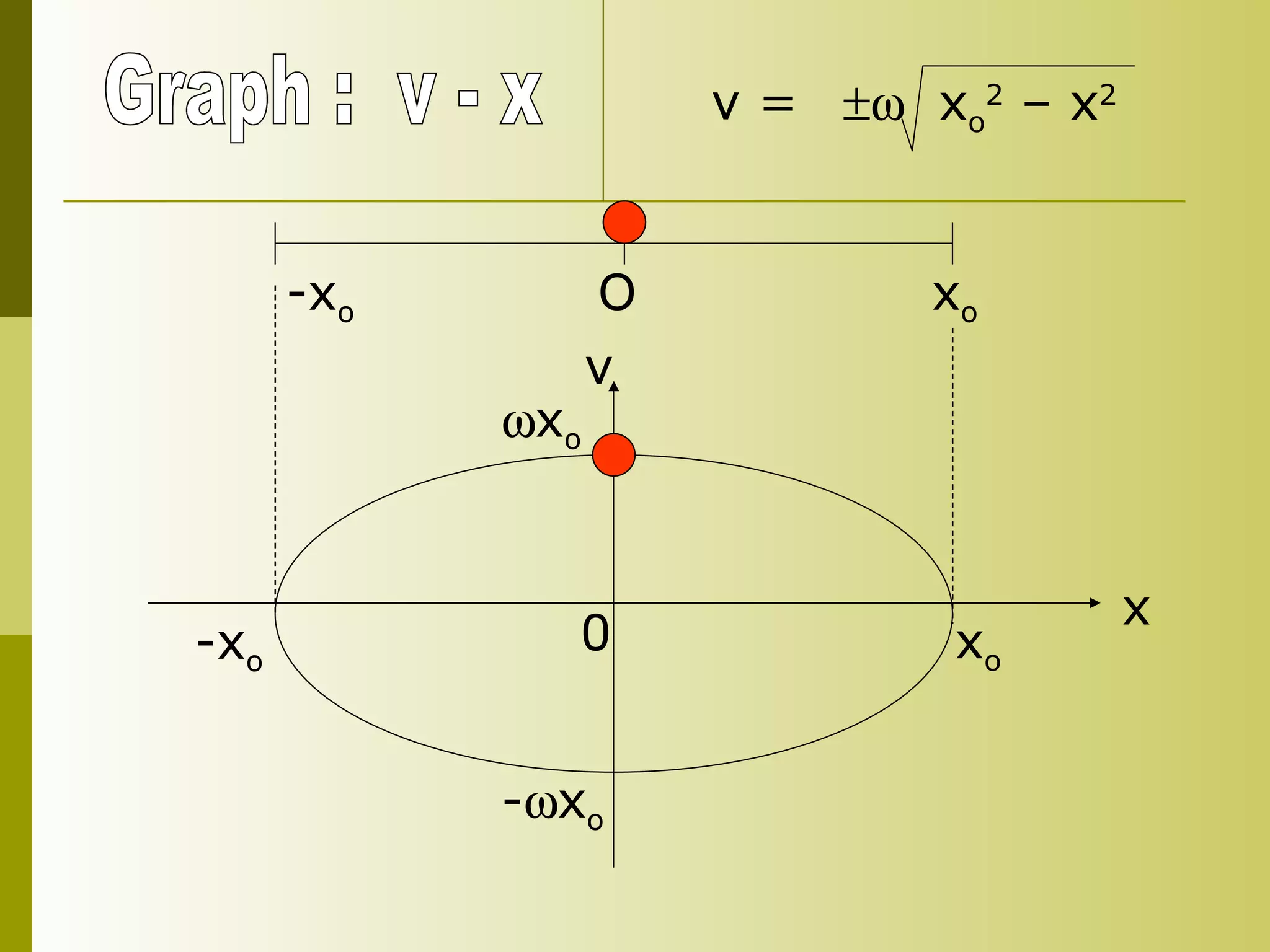
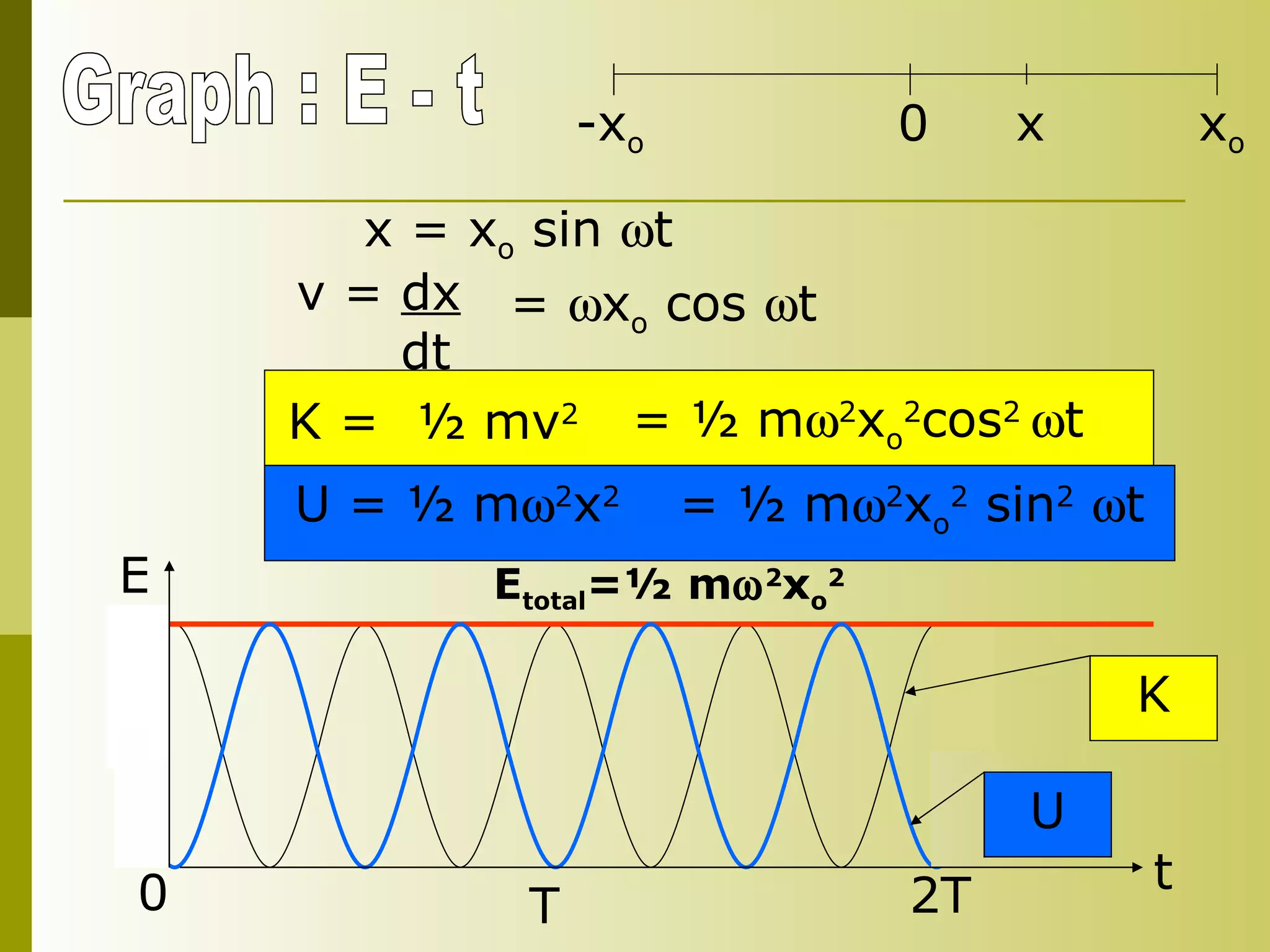
The document describes simple harmonic motion (SHM). Some key points: 1) SHM is motion where the acceleration is proportional to and directed towards the displacement from a fixed point. 2) Common examples include a vibrating tuning fork, weight on a spring, boy on a swing. 3) The motion can be defined by the force equation F = -kx, where k is the spring constant. 4) Kinematics equations for SHM include the position equation x = x0sin(ωt + φ) and related equations for velocity and acceleration.

1. Simple Harmonic Motion

2. Characteristics of Simple Harmonic Motion A body is in simple harmonic motion if its acceleration is proportional to its displacement from a fix point O, and is always directed towards that fixed point. a  – x a = –  2 x Negative sign : Direction of a is opposite to x O -x o x o a a

3. Some Common Examples of Simple Harmonic Motion Vibrating Tuning fork A weight on a spring A boy on a swing 200 grams

4. Definition : SHM may be defined as the motion of a body which is subjected to a resultant force which is directly proportional to the displacement of the body from a fixed point and always directed towards that fixed point F  – x F = – kx

5. O -x o x o Point of equilibrium : a = 0 F = 0 a x Measured from the point of equilibrium Amplitude : = x o =Maximum distance

6. Tutorial 24 Quick check 8.1 page 177

7. Kinematics of Simple Harmonic Motion F = - kx ma = - kx a = k m - x a = -  2 x compare  2 = k m  = angular frequency = 2  f = 2  T

8. F against x graph & a against x graph F x 0 x o -x o a x 0 x o -x o  2 x o -  2 x o F = -kx a = -  2 x

9. a = -  2 x d 2 x dt 2 = -  2 x x = x o sin (  t +  ) General solution dx dt =  x o cos (  t +  ) v = d 2 x dt 2 = -  2 x o sin (  t +  ) a = = -  2 x shown x = x o sin (  t +  ) phase  Phase constant

11. graph : x - t , v - t , a - t x t 0 x = x o sin  t x o -x o T 2T v T 0 -  x o  x o v =  x o cos  t t 2T a t 0 a = -  2 x o sin  t  2 x o -  2 x o T 2T t=0, v=  x o t=0, a=0

12. phase =  t +  /2 phase =  t phase x = x o sin  t v =  x o cos  t To compare the phase : They must all be expressed as same function (either as sine or cosine function) Phase difference : =(  t+ ) -  t  2 =  2 rad =  x o sin (  t +  /2) v leading x x t 0 x o -x o T 2T v T 0 -  x o  x o t 2T a t 0  2 x o -  2 x o T 2T

14. compare the motion x t 0 x o -x o T 2T v T 0 -  x o  x o t 2T a t 0  2 x o -  2 x o T 2T

15. example : -x o x o 0 t=0 x x = x o sin (  t +  ) General solution Substitute : t=0 , x = x o to find  x o = x o sin (  (0) +  ) sin  = 1  =  2 Therefore , equation of x is: x = x o sin (  t +  /2) t = x o cos  t

17. solution : x = 4.0 cos ( 2  t + )  3 a) i) Displacement = ? t = 2.0 s ; x = 4.0 cos ( 2  (2) + )  3 = 2.0 m ii) velocity = ? v = dx dt = -2  (4.0) sin ( 2  t + )  3 v = -8.0  sin (4  + ) t = 2.0 s ;  3 = -21.8 ms -1

18. solution : iii) acceleration = ? a = dv dt = -16.0  2 cos ( 2  t + )  3 t = 2.0 s ; a = -16.0  2 cos ( 2  (2) + )  3 = -79.0 ms -2 iv) Phase = ? x = 4.0 cos ( 2  t + )  3 Phase = 2  t +  3 t = 2.0 s ; Phase = 2  (2) +  3 = 13.6 rad

20. solution : x = 4.0 cos ( 2  t + )  3 b) i) frequency = ? x = x o cos (  t +  ) General solution : compare  = 2  2  f = 2  f = 1.0 Hz ii) Period = ? T = 1 f = 1.0 s

21. example : Figures (1) and (2) are the displacement-time graph and acceleration-time graph respectively of a body in simple harmonic motion. x,m 3 -3 t,s T 0 (1) a,ms -2 12 -12 t,s T 0 (2) What is the frequency of the motion? Write an expression to represent the variation of displacement x with time t.

22. solution : frequency = ? x o = 3  2 x o = 12  2 (3) = 12 substitute  = 2 rad s -1 2  f = 2 f = 0.318 Hz x,m 3 -3 t,s T 0 (1) a,ms -2 12 -12 t,s T 0 (2)

23. solution : expression = ? x = x o sin (  t +  ) General solution x o = 3 ,  = 2 ; x = 3 sin (2t +  ) At t = 0, x = 3 3 = 3 sin (2(0) +  ) sin  = 1  =  2 rad Therefore, the expression is x = 3 sin (2t + )  2 x = 3 cos 2t

24. variation of v with x a = dv = -  2 x dt dv x dx = -  2 x dx dt v dv = -  2 x dx   v 2 2 = -  2 x 2 2 + C When x = x o , v = 0 0 = -  2 x o 2 2 + C C =  2 x o 2 2 Hence ; v 2 2 = -  2 x 2 2  2 x o 2 2 + v 2 = -  2 x 2 +  2 x o 2 v =  x o 2 – x 2 v dv dx = -  2 x

25. Graph : v - x  x o -  x o x o -x o v x 0 -x o O x o v =  x o 2 – x 2

28. Tutorial 24 Quick check 8.1 and 8.2 page 177 and 183

29. energy in simple harmonic motion Total energy = E = K + U At point, x = 0 : K = ½ mv 2 = ½ m  2 (x o 2 – x 2 ) K = ½ m  2 (x o 2 – 0) = ½ m  2 x o 2 At point, x = 0 : U = 0 = maximum = ½ m  2 x o 2 + 0 = ½ m  2 x o 2 constant At point, x = x o : K = ½ m  2 (x o 2 –x o 2 ) = 0 = minimum -x o x o 0 x

30. energy in simple harmonic motion At any displacement,x E = K + U ½ m  2 x o 2 = ½ m  2 (x o 2 – x 2 ) + U = ½ m  2 x o 2 – ½ m  2 x 2 + U U = ½ m  2 x 2 -x o x o 0 x

31. Graph : E - x K max = ½ m  2 x o 2 U = ½ m  2 x 2 K min = 0 ; ; E total =½ m  2 x o 2 K=½ m  2 (x o 2 – x 2 ) U = ½ m  2 x 2 0 E x -x o x o -x o x o 0 x

32. Graph : F - x U = ½ m  2 x 2 F = – dU dx = – ½ (2) m  2 x = – m  2 x constant Therefore : F  x -x o x o m  x o -m  x o -x o x o 0 x 0 F x

33. Graph : E - t x = x o sin (  t +  ) General solution 0 = x o sin (  (0) +  ) At t = 0 , x = 0 0 = sin   = 0 x = x o sin  t Therefore : The equation is -x o x o 0 x

34. Graph : E - t x = x o sin  t v = dx dt =  x o cos  t K = ½ mv 2 = ½ m  2 x o 2 cos 2  t U = ½ m  2 x 2 = ½ m  2 x o 2 sin 2  t E total =½ m  2 x o 2 T 2T K U -x o x o 0 x 0 E t

35. Tutorial 25 Quick check 8.3 page 186