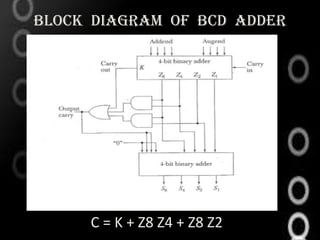
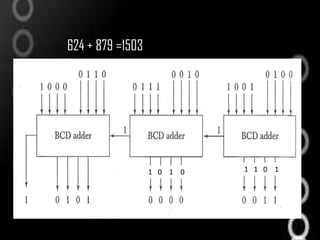
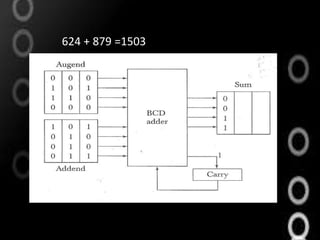
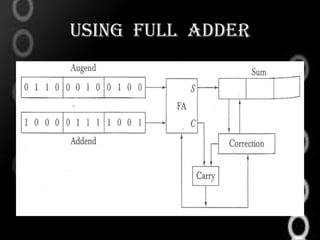
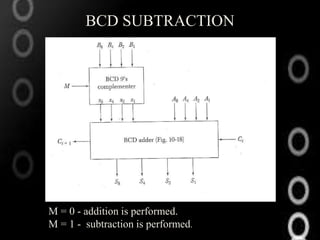
This document discusses decimal arithmetic operations using binary coded decimal (BCD) numbers. It describes how decimal numbers are represented in BCD format and processed using microoperations in the arithmetic logic unit (ALU). Addition and subtraction of decimal numbers are performed by converting the numbers to BCD, performing binary addition or subtraction on the digits, and converting the output back to decimal if needed. Block diagrams of BCD adders and examples of decimal addition and subtraction are provided.

1. DECIMAL ARITHEMATIC
OPERATIONS
PRESENTED BY :
PADMAPRIYA.G

2. INTRO
• Decimal numbers
INPUT
• Decimal numbers are placed in the registers in coded
form - Binary coded decimal (BCD )
ALU • Micro operations are performed
• Decimal numbers
output

3. DECIMAL ARITHEMATIC
MICROOPERATION SYMBOLS
 A A+B
Add contents of registers A and B, and
transfer the sum into A.
 B’
9’s complement of B.
 A A + B’ +1
content of A plus 10’s complement of B into A

4.  B B+ 1
Increment BCD number in B
 dshr A
Decimal shift right register A
 dshl A
Decimal shift left register A

5. ADDITION
BCD DIGITS
4 BIT BINARY ADDER
SUM : BINARY RANGING
FROM 0 TO 19

6. DERIVATION OF BCD ADDER
C = K + Z8 Z4 + Z8 Z2

7.  Output of binary adder : Binary form .
Conversion to BCD
Binary sum ≤ 1001 : no conversion
Binary sum ≥ 1001 : non valid BCD
add binary 6 (0110)
 3 different ways to add.

8. BLOCK DIAGRAM OF BCD ADDER
C = K + Z8 Z4 + Z8 Z2

9. Parallel decimal
addition
 BCD adders = digits in the number.
 Sum is formed in parallel.
 requires only 1 micro operations.

10. 624 + 879 =1503
1 0 1 0 1 1 0 1

11. DIGIT SERIAL, BIT PARALLEL
ADDITION
 Digits are applied to single BCD adder
serially.
Bits of each coded digit are transferred in
parallel.
For k digits – k micro operations.

12. 624 + 879 =1503

13. USING FULL ADDER

14. Example - ADDITION
6796 0110 0111 1001 0110
• 5368 + 0101 0011 0110 1000 +
• -----------------------------------------
1011 1010 1111 1110

15. 6796 0110 0111 1001 0110
5368 + 0101 0011 0110 1000 +
--------------------------------
1011 1010 1111 1110
0110 0110 0110 0110 +
-----------------------------------
10001 10000 10101 10100

16. 6796 0110 0111 1001 0110
5368 + 0101 0011 0110 1000 +
-------------------------------------------
1011 1010 1111 1110
0110 0110 0110 0110 +
-------------------------------------------
10001 10000 10101 10100
+
1 1 1 1
------------------------------------------------------
0001 0010 0001 0110 0100
------------------------------------------------------
1 2 1 6 4

17. SUBTRACTION
Using 9’s complement :
- Find 9’s complement of the –ve
number.
- Add the 2 numbers.
- IF result ≥ 10,add 6(0110).
- If the carry is generated add it with the
result, else find the 9’s complement of it.

18. Example
87 - 39
9’s complement of 39 = 99-39 = 60
87 1000 0111
60 0110 0000 +
--------------------
invalid 1110 0111

19. 87 1000 0111
60 0110 0000 +
------------------
•
1110 0111
0110
------- +
10100 0111
1+
--------------------
0100 1000
--------------------
4 8

20. 18 – 72
9’s complement of 72 = 99-72 =27
18 0001 1000
27 0010 0111
-----------------
0011 1111 invalid

21. 18 0001 1000
27 0010 0111
-----------------
0011 1111
0001 0110
------- -------
0100 (1)0101
------- --------
4 5
9’s complement of 45 = 54

22. USING 10’S COMPLEMENT
• Using 10’s complement :
- Find the 10’s complement of the number.
- Add the 2 numbers.
- If the result ≥ 10, add 6(0110).
- If the carry is not generated , then find
the 10’s complement of the result.

23. 34 – 56
10’s complement of 56 = (99-56)+1 = 44
34 0011 0100
44 0100 0100 +
---------------
0111 1000
7 8
10’s complement of 78 = 22

24. BCD SUBTRACTION
M = 0 - addition is performed.
M = 1 - subtraction is performed.