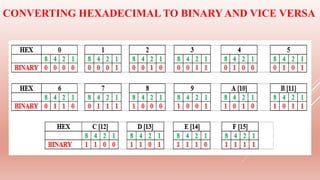
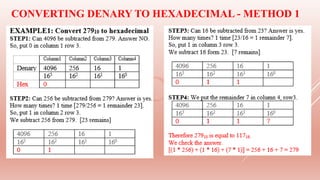
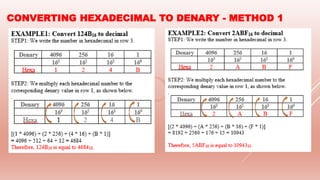
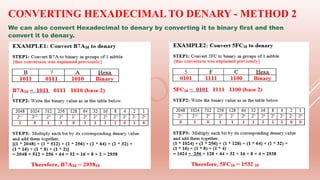
The document provides an overview of hexadecimal notation, explaining its advantages in representing positive numbers and facilitating conversions between hexadecimal, binary, and denary systems. It discusses practical applications in computing, such as color representation in HTML and MAC address formats. The document also elaborates on character encoding methods like ASCII and Unicode, emphasizing the efficiency of hexadecimal in programming and debugging.

1. UNIT 1.1.2- HEXADECIMAL
• represent positive numbers in hexadecimal notation
• show understanding of the reasons for choosing hexadecimal notation to
represent numbers
• convert positive hexadecimal integers to and from denary (a maximum of four
hexadecimal digits will be required)
• convert positive hexadecimal integers to and from binary (a maximum of 16-bit
binary numbers will be required)
• represent numbers stored in registers and main memory as hexadecimal
• identify current uses of hexadecimal numbers in computing, such as defining
colours in Hypertext Markup Language (HTML), Media Access Control (MAC)
addresses, assembly languages and machine code, debugging

2.  The word “Hexadecimal” means sixteen because this type of digital numbering
system uses 16 different digits from 0-to-9, and A-to-F. Hexadecimal numerals are
widely used as they are more human-friendlier. Each hexadecimal digit represents
four binary digits, also known as a nibble, which is half a byte.
 In a computer, each character is represented using a unique binary code. There
are different methods of encoding the characters, the 3 most common are: ASCII,
EBCDIC and UNICODE.
Binary value Hexadecimal value Denary value
0 0 0 0 0 0
0 0 0 1 1 1
0 0 1 0 2 2
0 0 1 1 3 3
0 1 0 0 4 4
0 1 0 1 5 5
0 1 1 0 6 6
0 1 1 1 7 7
1 0 0 0 8 8
1 0 0 1 9 9
1 0 1 0 A 10
1 0 1 1 B 11
1 1 0 0 C 12
1 1 0 1 D 13
1 1 1 0 E 14

3.  Using hexadecimal notation, digital numbers can be written using fewer digits
and with a much less likelihood of an error occurring.

 One of the most common Character sets is ASCII - American Standard Code for
Information Interchange.
Each character on the keyboard is represented by a binary number, this means
that when, for example the "H" key is pressed, the binary number 01001000 is
sent to the CPU. The CPU will then check the ASCII table to see which character
this is before outputting it in the desired location.
Number of bits
 Originally ASCII used only 7 bits to represent each character, this allowed for 128
different characters to be represented, this quickly became too little so an extra
bit was added. ASCII now uses 8 bits to represent each character, called the
extended ASCII.

4.  UNICODE
 To store English language, 256 characters is fine, however when it comes to other
languages in the world like Chinese, Arabic and special characters, there need to
be a character set to allow for these letters and other characters to be represented
and that is what Unicode is used for.
Unicode (16 bits) to represent each character, this allows for up to 65,536 different
characters to be represented, more than enough for every language and some
special characters.


5.  64-bit Unicode DataFlex will enable developers to create both 32-bit and 64-bit applications from the same source code.
Unicode will enable the use of 136,000 characters from 139 different written languages in DataFlex mobile, web and
Windows applications.

 USE OF THE HEXADECIMAL SYSTEM
 To describe locations in computer memory.
 In assembly language instructions.
 For memory readouts, values are also often in hexadecimal.
 Braille is coded in hexadecimal. {Note: Braille is a special character formed by raised dots, helping blind or partially
sighted people to type and read.}

 Why is Hex used?
 An 8-bit binary number can be represented by just two hex digits, with each hex digit representing 4 bits (a nibble).
 It is much simpler to write two digits than the full binary sequence, saving time and effort.

 ADVANTAGES OF USING HEXADECIMAL
 It is quicker for programmer to enter than binary.
 It is easier for programmer to understand and remember.
 It is very easy to convert binary to hexadecimal.

 For example:
1101 0100 in binary would be D 4 in hex
F F F F 3 in hex would be 1111 1111 1111 1111 0011 in binary

6. CONVERTING HEXADECIMAL TO BINARYAND VICE VERSA

7.  EXAMPLE1: Convert 1111100101010102
to hexadecimal.
 STEP1: Group the series of bits in
groups of 4 bits (1 nibble), starting from
right.
 111 1100 1010 1010

 STEP2: Add zero(s) to the first group of
bits to the extreme left to make it 4 bits
if necessary.
 0111 1100 1010 1010

 STEP3: Covert the nibble to
Hexadecimal.
 Answer: 7CAA
CONVERTING BINARY TO HEXADECIMAL
 EXAMPLE2: Convert
111111001010102 to hexadecimal.
 STEP1: Group the series of bits in
groups of 4 bits (1 nibble), starting from
right.
 11 1111 0010 1010
 STEP2: Add zero(s) to the extreme left
group of bits to make it 4 bits.
 0011 1111 0010 1010

 STEP3: Covert the nibble to
Hexadecimal.
 Answer: 3F2A

8.  EXAMPLE1: Convert BF9C16 to binary (see the conversion table above to
perform the conversion)

 BF9C16 = 1011 1111 1001 11002

 EXAMPLE2: Convert 5BA716 to binary

 FBA716 = 0101 1011 1010 01112

 EXAMPLE3: Convert DABE16 to binary

 DABE16 = 1101 1010 1011 11102
CONVERTING HEXADECIMAL TO BINARY

9.  Convert the following from
binary to hexadecimal.
 1111100010100001
 001101111011110
 110001010010111
 1001001110011100
 1110 01110011101
 Convert the following from
hexadecimal to denary.
 BFA9
 CB8A
 9ABC
 EBDC
 CABF
ACTIVITY 1

10. CONVERTING DENARY TO HEXADECIMAL - METHOD 1

11. EXAMPLE2: Convert 747010 to hexadecimal

12. CONVERTING DENARY TO HEXADECIMAL - METHOD 2
We can also convert denary to hexadecimal by converting it to binary first and then convert it to denary

13. 4562
589
9586
25639
19857
 987
 14589
 1293
 1024
 2512
ACTIVITY 2 - Convert the following from
denary to hexadecimal.

14. CONVERTING HEXADECIMAL TO DENARY - METHOD 1

15. CONVERTING HEXADECIMAL TO DENARY - METHOD 2
We can also convert Hexadecimal to denary by converting it to binary first and then
convert it to denary.

16. ACTIVITY 3 - Convert the following hexadecimal numbers
to denary.
i. 5DEF i. 2AFD i. 3EFB i. ABCF
i. 1BEC i. 4CB9 i. 3F7E viii. 2B5E

17. COLOURS IN HTML
All internet browsers use HTML and convert this into the webpage that you see in front of
you.
Colours are defined in html using the hex format.
Each of the three primary colors (i.e., red, green and blue) is represented by two
hexadecimal digits to create 255 possible values, thus resulting in more than 16 million
possible colors.
HTML code is often used to represent colours of text on the computer screen. The
different intensity of the three primary colours (red, green and blue) is determined by its
hexadecimal value. For example:

18. 
ACTIVITY 4:
Type any code above in notepad and save it as .html to
see how the code works.
EXAMPLE:
<font color="#FF0000"> RED </font> (RED)
Save it as test1.html

19. 
MEDIA ACCESS CONTROL (MAC)
It is a unique identifier assigned to network interfaces for
communication on the network. Hexadecimal numbers are used in
MAC address as it gives an unlimited number of possible
combinations to computer manufacturer. Each P.C in the world has
a unique identifier.
The MAC address is rarely changed so that a particular device can
always be identified no matter where it is. These numbers
(sometimes called "hardware addresses") are physically burned
into the network hardware during the manufacturing process, or
stored in firmware, and designed not to be modified.

20. 
FORMAT OF A MAC ADDRESS
MAC addresses are 12-digit (48-bits) hexadecimal numbers. Each hexadecimal number is 4
bits equivalent, so 4x12=48 bits. They are usually written in one of the following formats:
Each vendor registers and obtains MAC prefixes as assigned by the IEEE in charge of the international standards.
Vendors often possess many prefix numbers associated with their different products.
For example, the prefixes 00:13:10, 00:25:9C and 68:7F:74 (plus many others) all belong to Linksys (Cisco
Systems).
Note that hardware from different vendors may happen to share the same device portion of the address.
• 00 – 14 – 22 which identifies devices made by Dell
• 00 – 40 – 96 which identifies devices made by Cisco
• 00 – A0 – C9 which identifies devices made by Intel, and so on.

21. Types of MAC address
There are two types of MAC address: the UNIVERSALLY ADMINISTERED MAC
ADDRESS (UAA) and the LOCALLY ADMINISTERED MAC ADDRESS (LAA).
The UAA is the most common type of MAC address and this is the one set by the
manufacturer at the factory. It is rare for a user to want to change this MAC
address.
There are a few reasons why the MAC address needs to be changed using LAA:
• Certain software used on mainframe systems needs all the MAC addresses of
devices to fall into a strict format; because of this, it may be necessary to
change the MAC address of some devices to ensure they follow the correct
format.
• It may be necessary to bypass a MAC address filter on a router or a firewall;
only MAC addresses with a certain format are allowed through, otherwise the
devices will be blocked.
• To get past certain types of network restrictions it may be necessary to
emulate unrestricted MAC addresses; hence it may require the MAC address to be
changed on certain devices connected to the network.

22. ASSEMBLY CODE & MACHINE CODE
Computer memory can be referred to directly using machine code or assembly code. This can
have many advantages to
program developers or when carrying out troubleshooting. Machine code and assembly code
will be covered later but we are
simply interested in how hexadecimal fits in assembly and binary.
Using hexadecimal makes it much easier, faster and less error prone to write code compared
to binary. Example:
STO FFA4 (assembly code)
A5E4 FFA4 (machine code using hexadecimal values)
1010 0101 1110 0100 1111 1111 1010 0100 (machine code using binary)
Machine code and assembly code are examples of low-level languages.

25. THIS IS THE END OF UNIT 1.13
DATA STORAGE
YOU CAN GET MORE EXERCISES
FROM PAST EXAM PAPERS