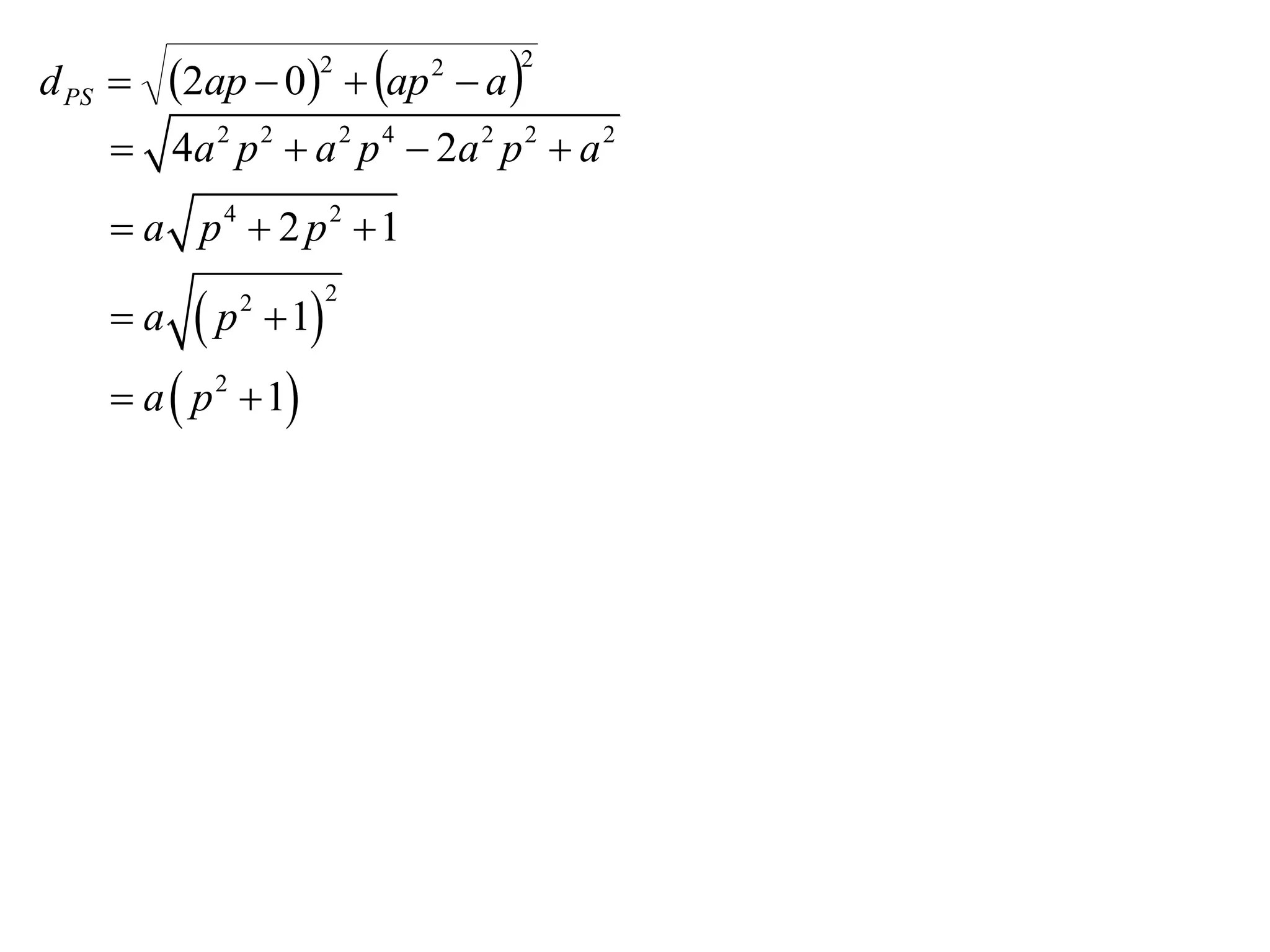The document discusses geometrical theorems about parabolas, including two main topics:
1) Focal chords - It proves that the tangents drawn from the extremities of a focal chord intersect at right angles on the directrix.
2) Reflection property - It discusses how any line parallel to the axis of the parabola is reflected towards the focus, and proves that the angle of incidence equals the angle of reflection.