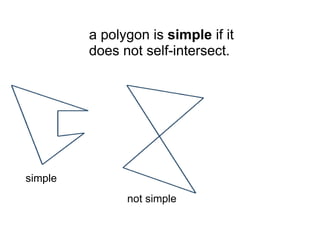
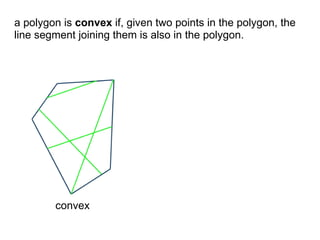
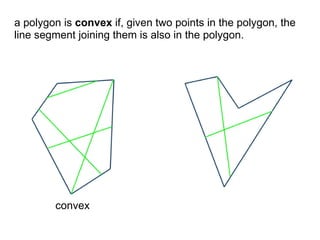
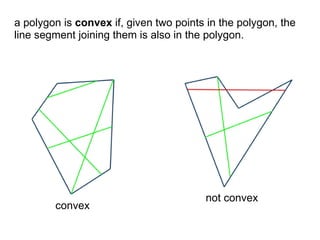
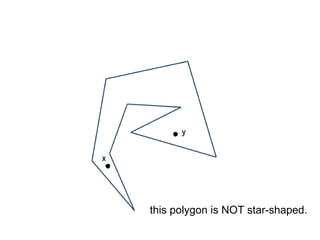
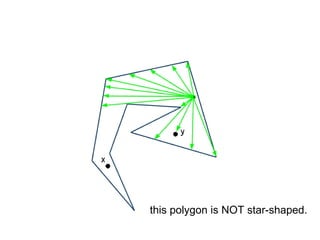
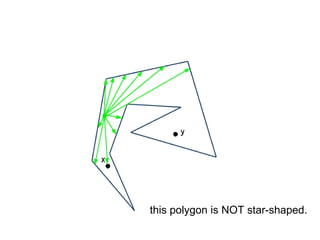
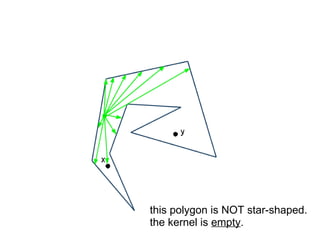
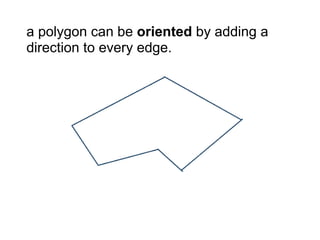
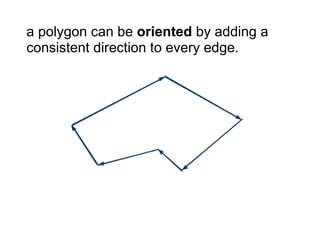
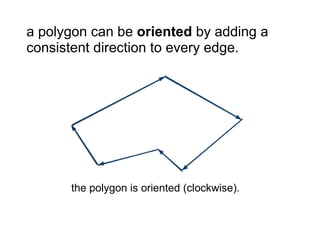
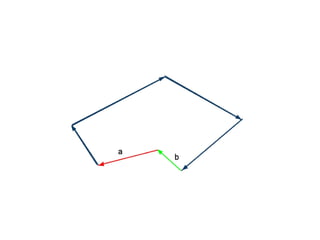
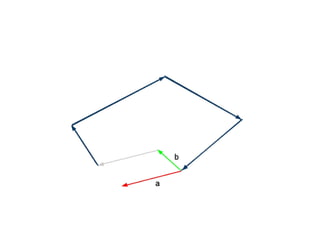
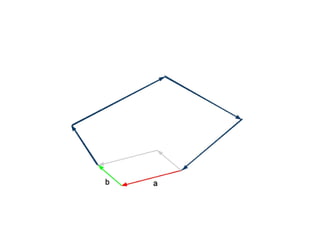
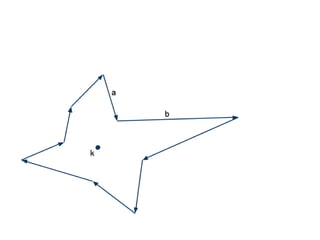
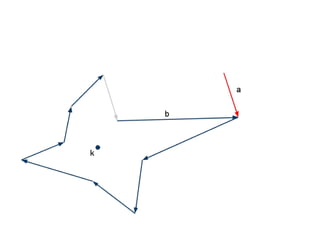
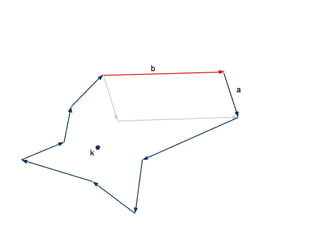
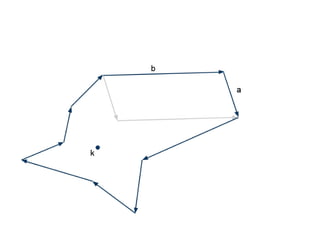
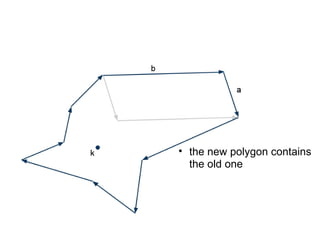
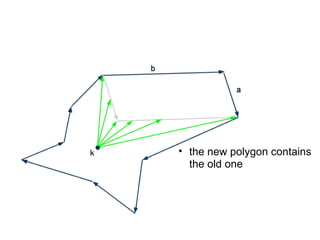
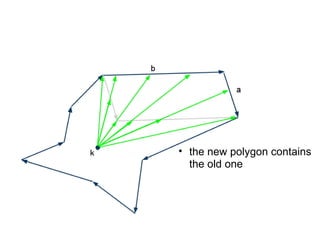
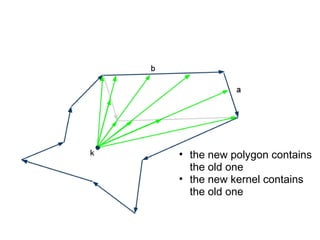
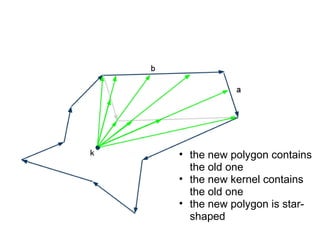
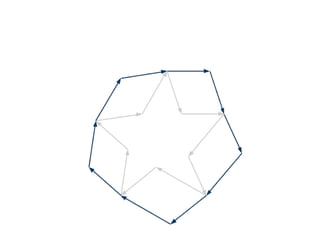
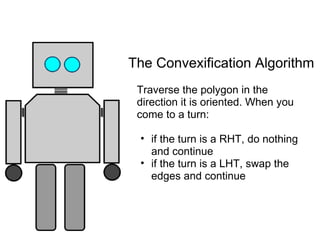
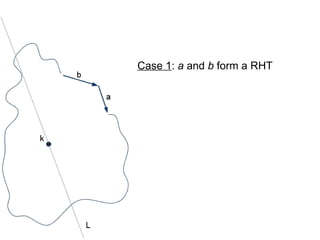
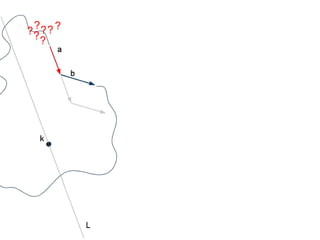
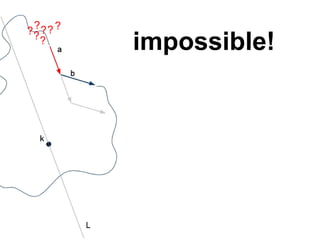
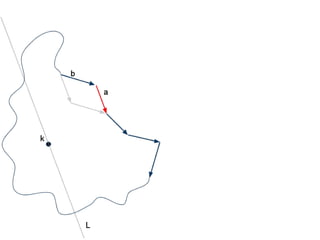
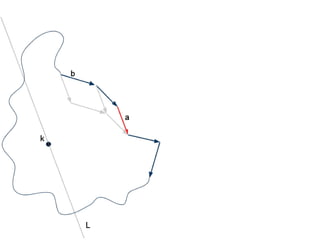
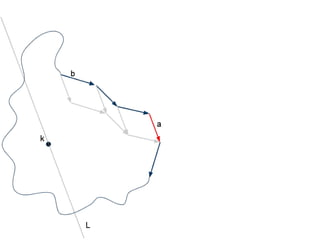
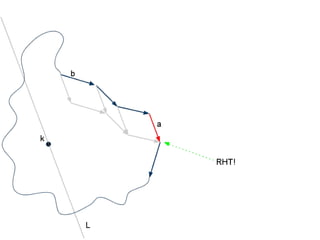
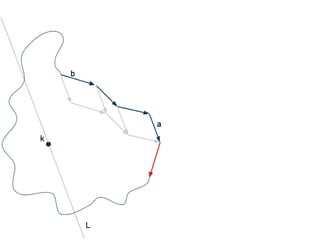
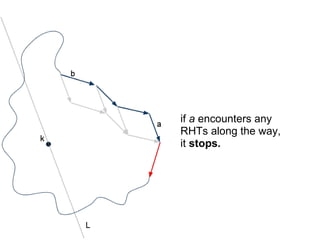
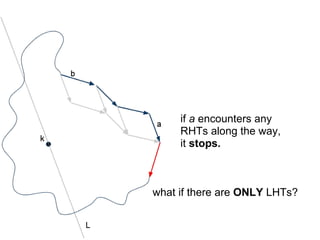
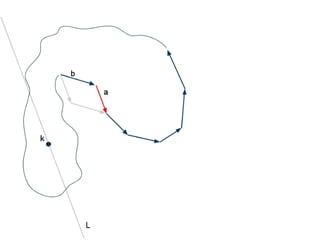
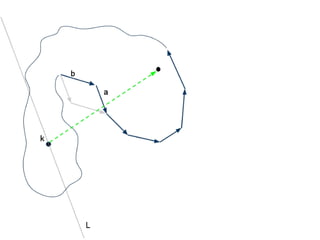
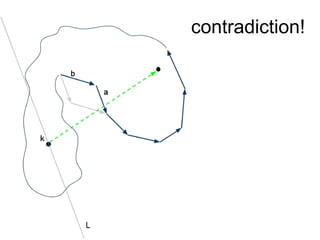
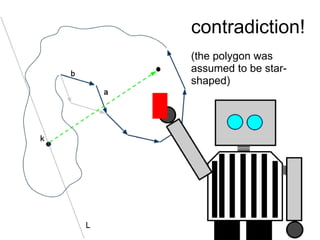
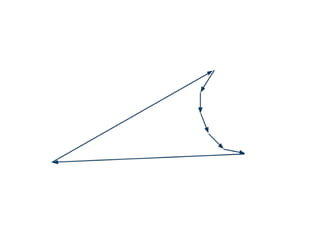
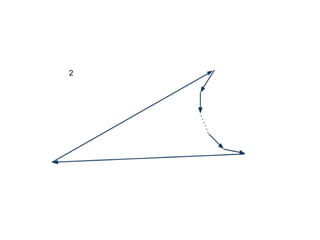
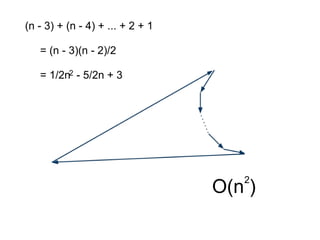
The document discusses different types of polygons including simple, convex, and star-shaped polygons. It then presents the convexification algorithm, which takes a star-shaped polygon and transforms it into a convex polygon through a series of edge swaps. The algorithm works by traversing the polygon and swapping any edges that form a left-hand turn. A proof is provided that this algorithm will always terminate with a convex polygon after at most n(n-1)/2 swaps, where n is the number of sides in the original polygon.

1. Permuting Polygons
Thomas Henderson
Under the direction of
Dr. Paul Latiolais
Second reader
Dr. Bin Jiang

2. types of
polygons

3. a polygon is simple if it
does not self-intersect.
simple

4. a polygon is simple if it
does not self-intersect.
simple
not simple

5. a polygon is simple if it
does not self-intersect.
simple really not
simple
not simple

6. a polygon is convex if, given two points in the polygon, the
line segment joining them is also in the polygon.

7. a polygon is convex if, given two points in the polygon, the
line segment joining them is also in the polygon.
convex

8. a polygon is convex if, given two points in the polygon, the
line segment joining them is also in the polygon.
convex

9. a polygon is convex if, given two points in the polygon, the
line segment joining them is also in the polygon.
convex

10. a polygon is convex if, given two points in the polygon, the
line segment joining them is also in the polygon.
not convex
convex

11. a polygon is star-shaped if all points in the
polygon can be seen from some point in the
polygon's interior.

12. a polygon is star-shaped if all points in the
polygon can be seen from some point in the
polygon's interior.
k

13. a polygon is star-shaped if all points in the
polygon can be seen from some point in the
polygon's interior.
k

14. a polygon is star-shaped if all points in the
polygon can be seen from some point in the
polygon's interior.
k k is in the
kernel of the
polygon.

15. this polygon is NOT star-shaped.

16. this polygon is NOT star-shaped.

17. this polygon is NOT star-shaped.

18. this polygon is NOT star-shaped.
the kernel is empty.

19. a polygon can be oriented by adding a
direction to every edge.

20. a polygon can be oriented by adding a
consistent direction to every edge.

21. a polygon can be oriented by adding a
consistent direction to every edge.
the polygon is oriented (clockwise).

22. edge swaps

26. let P be a clockwise-oriented,
star-shaped polygon.
let a and b be edges of P which
are adjacent, and which form a
left-hand turn.
let k be a point in the kernel of P.

31. • the new polygon contains
the old one

32. • the new polygon contains
the old one

33. • the new polygon contains
the old one

34. • the new polygon contains
the old one

35. • the new polygon contains
the old one
• the new kernel contains
the old one

36. • the new polygon contains
the old one
• the new kernel contains
the old one
• the new polygon is star-
shaped

37. convexification

38. Problem: Given a star-
shaped polygon, can you
make it a
convex polygon by
swapping edges?

39. Problem: Given a star-
shaped polygon, can you
make it a
convex polygon by
swapping edges?
no, seriously: can you?

40. Instructions:
• Make a star-shaped polygon.
• Turn it into a convex polygon.
You may ONLY swap adjacent
edges!

41. Instructions:
• Make a star-shaped polygon.
• Turn it into a convex polygon.
You may ONLY swap adjacent
edges!
go!

44. The Convexification Algorithm

45. The Convexification Algorithm
Traverse the polygon in the
direction it is oriented. When you
come to a turn:
• if the turn is a RHT, do nothing
and continue
• if the turn is a LHT, swap the
edges and continue

46. Theorem: The Convexification
Algorithm will convexify any
star-shaped polygon.

47. The Idea of the Proof:
Show that any two edges
of any star-shaped
polygon will be swapped
at most once.

48. let P be a clockwise-oriented, star-shaped
polygon.
let a and b be edges of P which are adjacent.
let k be a point in the kernel of P.
let L be a line through k, and parallel to a.

49. Case 1: a and b form a RHT

50. Case 1: a and b form a RHT

51. Case 1: a and b form a RHT
ZERO
SWAPS

52. Case 2: a and b form a LHT

53. Case 2: a and b form a LHT

54. Case 2: a and b form a LHT

55. ONE SWAP

56. ?
?? ? ? ?
?

57. ?
?? ? ? ?
?
impossible!

63. if a encounters any
RHTs along the way,
it stops.

64. if a encounters any
RHTs along the way,
it stops.
what if there are ONLY LHTs?

67. contradiction!

68. contradiction!
(the polygon was
assumed to be star-
shaped)

69. analysis of
algorithms

70. What is the worst possible
behavior of the Convexification
Algorithm?

72. What is the worst possible
behavior of the Convexification
Algorithm?

73. Suppose P has n sides. If the
algorithm must swap every side
with every other side, the number
of swaps is
(n - 1) + (n - 2) + ... + 2 + 1
= n(n - 1)/2
= n2 /2 - n/2

74. Suppose P has n sides. If the
algorithm must swap every side
with every other side, the number
of swaps is
(n - 1) + (n - 2) + ... + 2 + 1
= n(n - 1)/2 2
= n2 /2 - n/2
O(n )

76. 2

77. (n - 3) + (n - 4) + ... + 2 + 1
= (n - 3)(n - 2)/2
= 1/2n2 - 5/2n + 3
2
O(n )