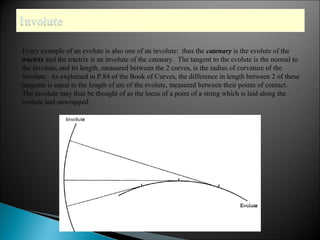
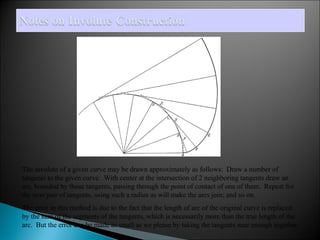
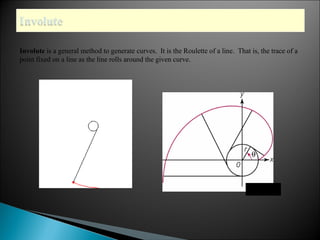
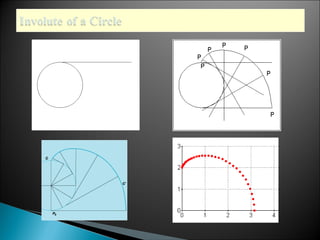
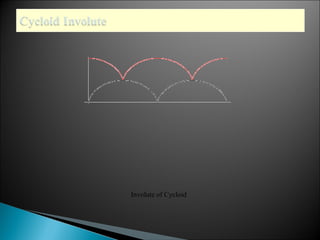
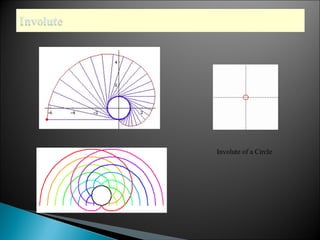
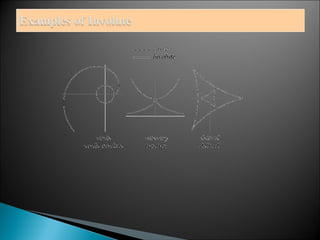
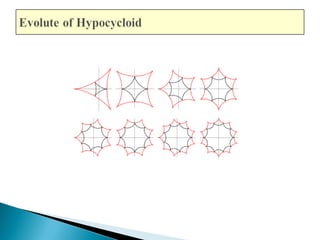
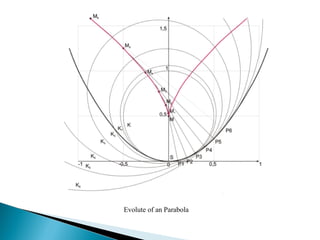
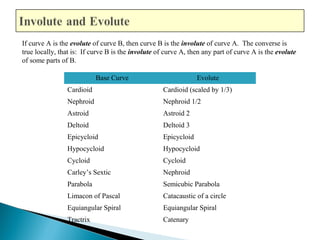
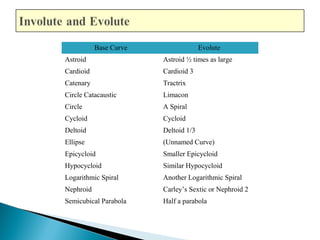
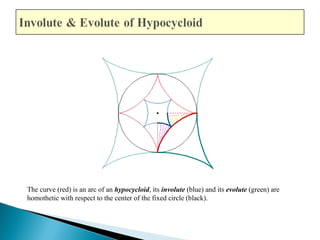
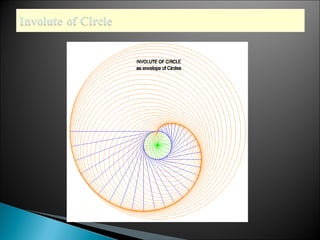
The document discusses evolutes and involutes of curves. It defines an evolute as the locus of the centers of curvature of a curve, and an involute as a curve that is traced by a point on a taut string unwinding from the evolute. Specifically: - The evolute of a curve is the envelope of its normals, and the original curve is the involute of its evolute. - Examples of evolutes include the semi-cubic parabola as the evolute of a parabola, and an equal spiral as the evolute of an equiangular spiral. 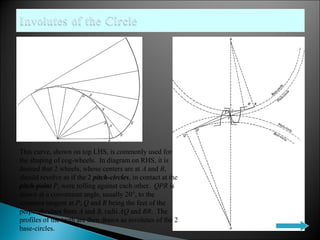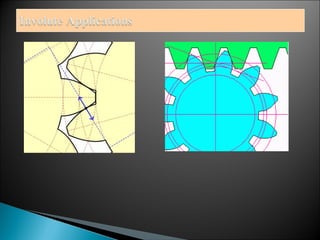- Involutes can be used to generate gear teeth profiles, with the teeth profiles drawn as invol

1. Tanuj Parikh

3.  Introduction
 Involutes
 Evolutes
 Involute vs. Evolute

5. If the normals at points Q and q of a curve meet at C, then the limiting position of C, as q
approaches Q, is called the center of curvature of the curve at Q.
The locus of the center of curvature, as Q varies on the curve, is called the evolute of the curve.
The original curve is called an involute of the new one.
The evolute may alternatively be defined as the envelope of the normal to the curve; for C lies on
2 tangents to this envelop and, as they approach coincidence, the limiting position of C is a point
on the envelope.
Evolute Examples
Many examples have already been given, such as the evolute of the parabola and that of the
cycloid. It has been shown that the evolute of an equiangular spiral is an equal spiral; and the
evolute of any hypocycloid or epicycloid is a curve similar to the original.

6. In the drawing of evolutes it is a help to know that the evolute passes through any ordinary cusp-point
of the original curve; that points of inflexion on the original curve correspond to points at
infinity on the evolute; and that points of maximum or minimum curvature correspond to cusps of
the evolute.
To draw an evolute it is necessary to have some means of drawing accurately a number of normals
to the original curve. Sometimes this can be done by a knowledge of the geometry of the curve as,
for example, for the parabola, and the cycloidal curves.
The evolutes of roulettes and glissettes can usually be drawn, because the position of the
instantaneous center is known and the normal can therefore be drawn. This applies to such curves
as the right strophoid and all conchoids and negative pedals.

7. The following curves are suggested among those whose evolutes can be drawn:
 The ellipse. With any point on the minor axis as center draw a circle passing through the loci,
cutting the curve at P and the further part of the minor axis at G. Then PG is a normal to the
ellipse at P.
 The limacon. With the notation of P.45 of Book of Curves the instantaneous center of PP’,
regarded as a moving rod, is on the base-circle, at the point I opposite to Q. Hence IP and IP’
are normals.
 The lemniscate. If the curve is drawn by the method of P.115 of Book of Curves, the
instantaneous center of MM’ is at the intersection of CM and C’M’. The line drawn from this
point to P is a normal to the curve
 The right strophoid. The following method is suggested: Let OA and AD be 2 lines at right
angles, O being a fixed point about 2 inches from A. With center at any point W on OA
produced, and radius WO, draw an arc cutting AD at Q. With the same radius, and centers at
O and Q, draw arcs intersecting at T (so that OWQT is a rhombus). Join WQ and mark off WP
on it equal to WA. Join PT. Then the locus of T is a parabola; that of P is a strophoid; and PT
is a normal to the strophoid. (Note: The position of W should be moved towards A and past A,
until it is half-way between A and O; but, after it has passed A, WP must be marked off along
QW produced.) (Hint for proof: In Figure 66, P.93 of the Book of Curves, T is the
instantaneous center of the moving set square.

8. Every example of an evolute is also one of an involute: thus the catenary is the evolute of the
tractrix and the tractrix is an involute of the catenary. The tangent to the evolute is the normal to
the involute, and its length, measured between the 2 curves, is the radius of curvature of the
involute. As explained in P.84 of the Book of Curves, the difference in length between 2 of these
tangents is equal to the length of arc of the evolute, measured between their points of contact.
The involute may thus be thought of as the locus of a point of a string which is laid along the
evolute and unwrapped.

9. The involute of a given curve may be drawn approximately as follows: Draw a number of
tangents to the given curve. With center at the intersection of 2 neighboring tangents draw an
arc, bounded by those tangents, passing through the point of contact of one of them. Repeat for
the next pair of tangents, using such a radius as will make the arcs join; and so on.
The error in this method is due to the fact that the length of arc of the original curve is replaced
by the sum of the segments of the tangents, which is necessarily more than the true length of the
arc. But the error can be made as small as we please by taking the tangents near enough together.

10. This curve, shown on top LHS, is commonly used for
the shaping of cog-wheels. In diagram on RHS, it is
desired that 2 wheels, whose centers are at A and B,
should revolve as if the 2 pitch-circles, in contact at the
pitch-point P, were rolling against each other. QPR is
drawn at a convenient angle, usually 20°, to the
common tangent at P; Q and R being the feet of the
perpendiculars from A and B, radii AQ and BR. The
profiles of the teeth are then drawn as involutes of the 2
base-circles.

11. Proof:
To see the reasoning in last foil, with the teeth
in contact, the wheels will in fact revolve as if
the pitch-circles were rolling against each
other, consider 2 points Q’ and R’ which will
move to the positions Q and R in the same
interval of time. If the tangents to the base-circles
at Q’ and R’ are Q’Y and R’Z,
Q’Y + ZR’ = QP + PR.
But O’Y = arc Q’Q + QP and
ZR’ = PR – arc R’R (construction).
Therefore arc Q’Q = arc R’R, and it follows
that Q and R move with equal velocities. As
the radii are in proportion, points fixed on the
pitch-circles will also move with equal
velocities.

12. While every curve has but one evolute, it has many involutes; for the initial point, where the
involute cuts the original curve, may be chosen arbitrarily. The various curves so obtained are
called parallel curves. Any 2 of them are a constant distance apart, the distance being measured
along the common normal. The involutes of a circle are all identical, but in other cases varying
shapes are produced. To draw curves parallel to a given curve it is only necessary to draw a
number of normals and to mark off equal distances along each of them.

13. It may be noted, in drawing involutes, a cusp may occur either at the initial point (i.e. the point
where the involute meets the original curve) or at a point corresponding to a point of inflexion of
the original curve. In drawing a curve parallel to a given curve, a cusp may be found at a point
where the radius of curvature of the original curve is equal to the constant distances between the
curves.
The following are suggested for drawing:
1. An involute of the circle.
2. Involutes of the nephroid (i) with the initial point mid-way between 2 cusps, (ii) with the
initial point at a cusp-point.
3. An involute of the lemniscate, with the initial point at one end of the transverse axis.
4. Curves parallel to the parabola, with the constant distance measured along the inward
normal and (i) equal to 2a (a being the distance from the focus to the vertex), (ii) greater
than 2a.
5. Curves parallel to the ellipse, with the constant distance measured along the inward normal
and (i) between b2 / a and a2 / b, (ii) great than a2 / b.
6. Curves parallel to the astroid, at varying distances.

14. Base Curve Evolute
Parabola Semi-cubic Parabola
Ellipse or Hyperbola Lame Curve
Cycloid An equal Cycloid
Epicycloid
A similar Epicycloid
Hypocycloid A similar Hypocycloid
Cayley’s Sextic Nephroid
Equiangular Spiral An equal spiral
Tractrix Catenary
2
1 3
2
3
y
ö çè
= ÷ø
x
ö çè
æ + ÷ø
æ
B
A

16. Involute is a general method to generate curves. It is the Roulette of a line. That is, the trace of a
point fixed on a line as the line rolls around the given curve.

18. Involute of Cycloid

19. Involute of a Circle

22. Involute of a Sine Curve

26. Evolute is a method of deriving a new curve based on a given curve. It is the locus of the
centers of tangent circles of the given circle. Evolute of a curve can also be defined as the
envelope of its normal.
Evolute of an Ellipse

28. Evolute of an Parabola

29. Evolute of a Hypotrochoid

31. If curve A is the evolute of curve B, then curve B is the involute of curve A. The converse is
true locally, that is: If curve B is the involute of curve A, then any part of curve A is the evolute
of some parts of B.
Base Curve Evolute
Cardioid Cardioid (scaled by 1/3)
Nephroid Nephroid 1/2
Astroid Astroid 2
Deltoid Deltoid 3
Epicycloid Epicycloid
Hypocycloid Hypocycloid
Cycloid Cycloid
Carley’s Sextic Nephroid
Parabola Semicubic Parabola
Limacon of Pascal Catacaustic of a circle
Equiangular Spiral Equiangular Spiral
Tractrix Catenary

32. Base Curve Evolute
Astroid Astroid ½ times as large
Cardioid Cardioid 3
Catenary Tractrix
Circle Catacaustic Limacon
Circle A Spiral
Cycloid Cycloid
Deltoid Deltoid 1/3
Ellipse (Unnamed Curve)
Epicycloid Smaller Epicycloid
Hypocycloid Similar Hypocycloid
Logarithmic Spiral Another Logarithmic Spiral
Nephroid Carley’s Sextic or Nephroid 2
Semicubical Parabola Half a parabola

33. The curve (red) is an arc of an epicycloid, its involute (blue) and its evolute (green) are
homothetic with respect to the center of the fixed circle (black).

34. The curve (red) is an arc of an hypocycloid, its involute (blue) and its evolute (green) are
homothetic with respect to the center of the fixed circle (black).