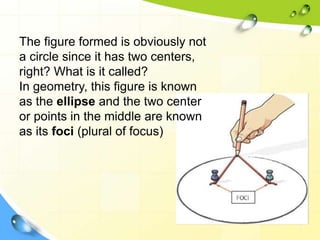
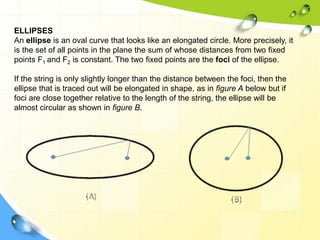
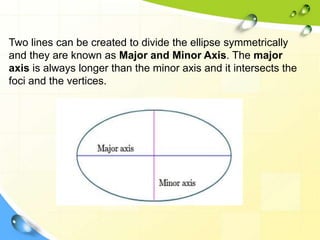
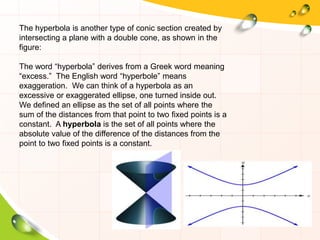
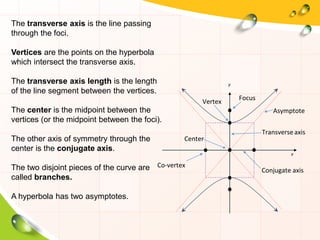
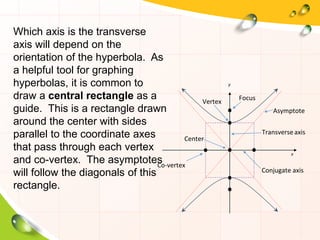
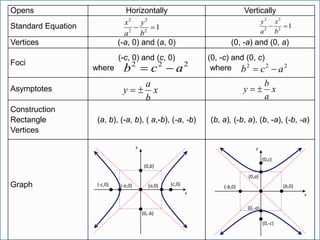
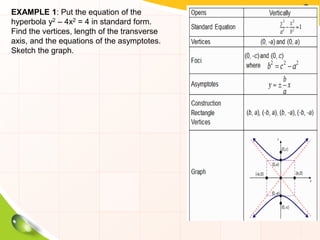
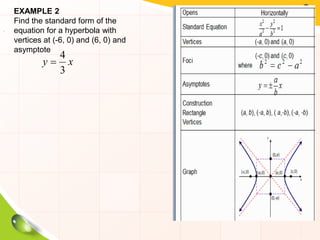
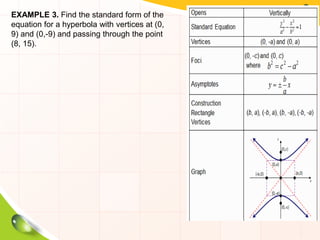
This document provides information about ellipses and hyperbolas. It defines ellipses as sets of points where the sum of the distances to two fixed foci is a constant. Hyperbolas are defined as sets of points where the difference of distances to two foci is a constant. The document gives equations and properties of ellipses and hyperbolas like foci, vertices, axes, asymptotes. It includes examples of finding standard forms of equations and graphing ellipses and hyperbolas given properties.

1. L/O/G/O
y
x
L1
L2
(x1,
y1)
x
1
y
1
𝜋
𝒌=𝟎
𝟐
𝟏
𝑥 =
−𝑏 ± 𝑏2 − 4𝑎𝑐
2𝑎
0
5

2. 2nd 4th
3rd
1st
Pre- Calculus
Week 3-4
Tchr. James Luck M. Valenzuela

3. The figure formed is obviously not
a circle since it has two centers,
right? What is it called?
In geometry, this figure is known
as the ellipse and the two center
or points in the middle are known
as its foci (plural of focus)

4. ELLIPSES
An ellipse is an oval curve that looks like an elongated circle. More precisely, it
is the set of all points in the plane the sum of whose distances from two fixed
points F1 and F2 is constant. The two fixed points are the foci of the ellipse.
If the string is only slightly longer than the distance between the foci, then the
ellipse that is traced out will be elongated in shape, as in figure A below but if
foci are close together relative to the length of the string, the ellipse will be
almost circular as shown in figure B.

5. Two lines can be created to divide the ellipse symmetrically
and they are known as Major and Minor Axis. The major
axis is always longer than the minor axis and it intersects the
foci and the vertices.

6. The equation for an ellipse with a
horizontal major axis is given by
𝒙𝟐
𝒂𝟐
+
𝒚𝟐
𝒃𝟐
= 𝟏
where a is the length from the center
of the ellipse to the end the major
axis, and b is the length from the
center to the end of the minor axis.
The foci of the ellipse (with horizontal
major axis) are at (-c,0) and (c,0),
where c is given by:
c= 𝑎2 − 𝑏2
The vertices of an ellipse are at (−a,
0) and (a, 0).

7. ELLIPSE WITH CENTER AT THE ORIGIN
Equation
𝒙𝟐
𝒂𝟐 +
𝒚𝟐
𝒃𝟐 = 𝟏
𝒙𝟐
𝒃𝟐 +
𝒚𝟐
𝒂𝟐 = 𝟏
a > b > 0 a > b > 0
Vertices (±a, 0) (0, ±a)
Major Axis Horizontal, length 2a Vertical, length 2a
Minor Axis Vertical, length 2b Horizontal, length 2b
Foci (±c, 0), c2 = a2 – b2 (0, ±c), c2 = a2 – b2

8. ELLIPSE WITH CENTER AT THE ORIGIN
Equation
𝒙𝟐
𝒂𝟐 +
𝒚𝟐
𝒃𝟐 = 𝟏
𝒙𝟐
𝒃𝟐 +
𝒚𝟐
𝒂𝟐 = 𝟏
a > b > 0 a > b > 0
Vertices (±a, 0) (0, ±a)
Major Axis Horizontal, length 2a Vertical, length 2a
Minor Axis Vertical, length 2b Horizontal, length 2b
Foci (±c, 0), c2 = a2 – b2 (0, ±c), c2 = a2 – b2
EXAMPLE 1
An ellipse has the equation
𝒙𝟐
𝟗
+
𝒚𝟐
𝟒
= 𝟏
Find the foci, the vertices, and the
lengths of the major and minor axes
and sketch the graph.

9. EXAMPLE 2
Find the foci of the
ellipse 16x2 + 9y2 = 144,
and sketch its graph.
ELLIPSE WITH CENTER AT THE ORIGIN
Equation
𝒙𝟐
𝒂𝟐 +
𝒚𝟐
𝒃𝟐 = 𝟏
𝒙𝟐
𝒃𝟐 +
𝒚𝟐
𝒂𝟐 = 𝟏
a > b > 0 a > b > 0
Vertices (±a, 0) (0, ±a)
Major Axis Horizontal, length 2a Vertical, length 2a
Minor Axis Vertical, length 2b Horizontal, length 2b
Foci (±c, 0), c2 = a2 – b2 (0, ±c), c2 = a2 – b2

10. EXAMPLE 3
The vertices of an ellipse
are (±4, 0) and the foci are
(± 2,0). Find its equation
and sketch the graph
ELLIPSE WITH CENTER AT THE ORIGIN
Equation
𝒙𝟐
𝒂𝟐 +
𝒚𝟐
𝒃𝟐 = 𝟏
𝒙𝟐
𝒃𝟐 +
𝒚𝟐
𝒂𝟐 = 𝟏
a > b > 0 a > b > 0
Vertices (±a, 0) (0, ±a)
Major Axis Horizontal, length 2a Vertical, length 2a
Minor Axis Vertical, length 2b Horizontal, length 2b
Foci (±c, 0), c2 = a2 – b2 (0, ±c), c2 = a2 – b2

11. EXAMPLE 4
Find the equation of an Ellipse from its
Eccentricity and Foci.
Find the equation of the ellipse with
foci (0, ±8) and eccentricity𝑒 =
4
5
, and
sketch its graph.
ELLIPSE WITH CENTER AT THE ORIGIN
Equation
𝒙𝟐
𝒂𝟐 +
𝒚𝟐
𝒃𝟐 = 𝟏
𝒙𝟐
𝒃𝟐 +
𝒚𝟐
𝒂𝟐 = 𝟏
a > b > 0 a > b > 0
Vertices (±a, 0) (0, ±a)
Major Axis Horizontal, length 2a Vertical, length 2a
Minor Axis Vertical, length 2b Horizontal, length 2b
Foci (±c, 0), c2 = a2 – b2 (0, ±c), c2 = a2 – b2

13. The hyperbola is another type of conic section created by
intersecting a plane with a double cone, as shown in the
figure:
The word “hyperbola” derives from a Greek word meaning
“excess.” The English word “hyperbole” means
exaggeration. We can think of a hyperbola as an
excessive or exaggerated ellipse, one turned inside out.
We defined an ellipse as the set of all points where the
sum of the distances from that point to two fixed points is a
constant. A hyperbola is the set of all points where the
absolute value of the difference of the distances from the
point to two fixed points is a constant.

14. The transverse axis is the line passing
through the foci.
Vertices are the points on the hyperbola
which intersect the transverse axis.
The transverse axis length is the length
of the line segment between the vertices.
The center is the midpoint between the
vertices (or the midpoint between the foci).
The other axis of symmetry through the
center is the conjugate axis.
The two disjoint pieces of the curve are
called branches.
A hyperbola has two asymptotes.
x
y
Vertex
Focus
Asymptote
Center
Co-vertex
Transverse axis
Conjugate axis

15. x
y
Vertex
Focus
Asymptote
Center
Co-vertex
Transverse axis
Conjugate axis
Which axis is the transverse
axis will depend on the
orientation of the hyperbola. As
a helpful tool for graphing
hyperbolas, it is common to
draw a central rectangle as a
guide. This is a rectangle drawn
around the center with sides
parallel to the coordinate axes
that pass through each vertex
and co-vertex. The asymptotes
will follow the diagonals of this
rectangle.

16. Opens Horizontally Vertically
Standard Equation
Vertices (-a, 0) and (a, 0) (0, -a) and (0, a)
Foci
(-c, 0) and (c, 0)
where
(0, -c) and (0, c)
where
Asymptotes
Construction
Rectangle
Vertices
(a, b), (-a, b), ( a,-b), (-a, -b) (b, a), (-b, a), (b, -a), (-b, -a)
Graph
1
2
2
2
2


b
y
a
x 1
2
2
2
2


b
x
a
y
2
2
2
a
c
b 

x
a
b
y 

x
b
a
y 

x
y
(0,b)
(-c,0)
(0,-b)
(c,0)
(a,0)
(-a,0)
x
y
(0,a)
(0,c)
(-b,0)
(0,-a)
(0,-c)
(b,0)
2
2
2
a
c
b 


17. EXAMPLE 1: Put the equation of the
hyperbola y2 – 4x2 = 4 in standard form.
Find the vertices, length of the transverse
axis, and the equations of the asymptotes.
Sketch the graph.

18. EXAMPLE 2
Find the standard form of the
equation for a hyperbola with
vertices at (-6, 0) and (6, 0) and
asymptote
x
y
3
4

.

19. EXAMPLE 3. Find the standard form of the
equation for a hyperbola with vertices at (0,
9) and (0,-9) and passing through the point
(8, 15).