This document discusses different numeral systems including binary, decimal, and hexadecimal. 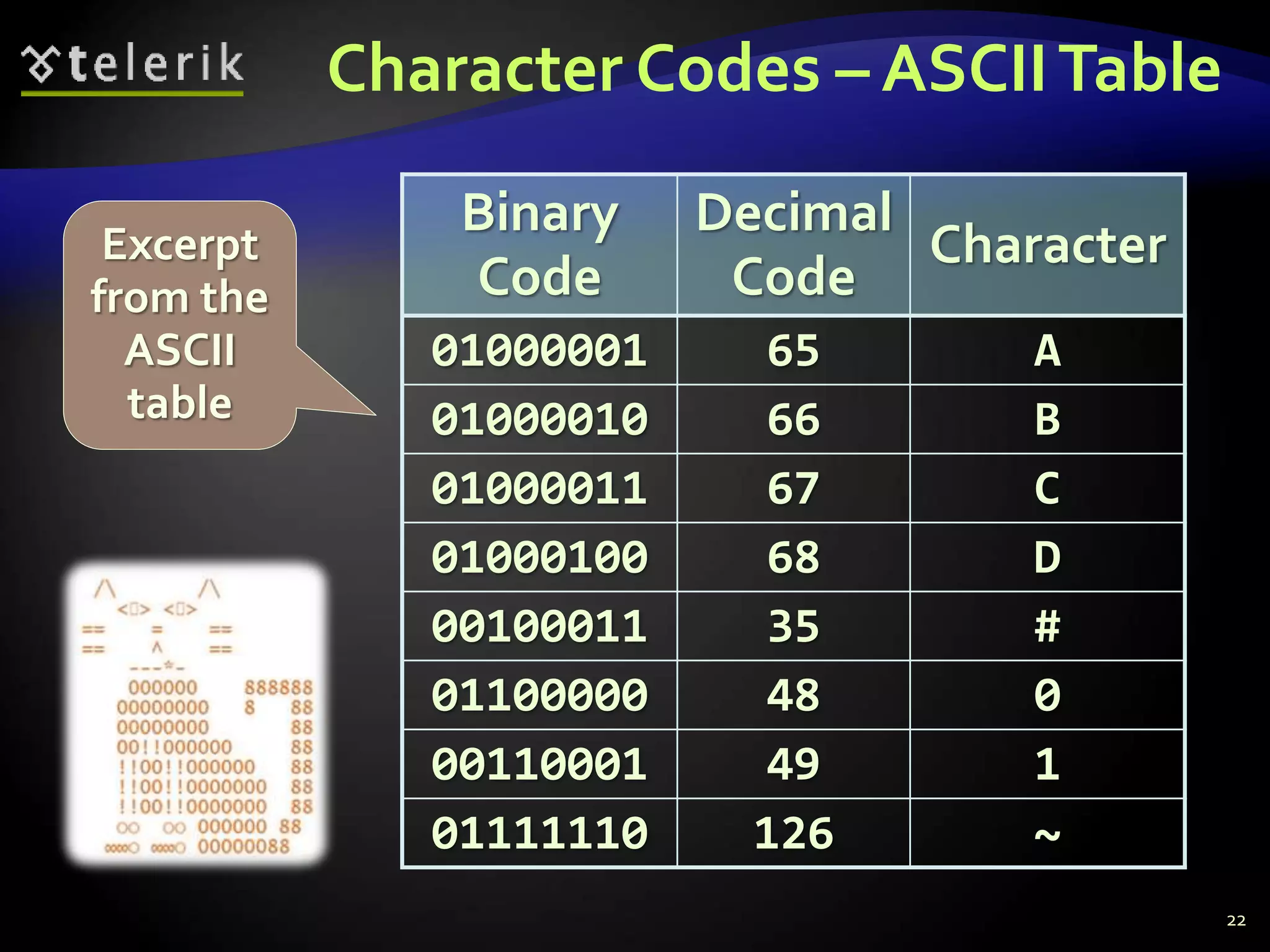It provides details on: - How each system represents numbers using different bases and numerals - Converting between the numeral systems by multiplying digits by their place value or dividing and taking remainders - How computers internally represent integer and floating-point numbers, including sign representation and IEEE 754 standard - How text is encoded using character codes like ASCII and stored as strings with null terminators

1. Numeral Systems
Binary, Decimal and Hexadecimal Numbers
Svetlin Nakov
Telerik Corporation
www.telerik.com

2. Table of Contents
1. Numerals Systems
Binary and Decimal Numbers
Hexadecimal Numbers
Conversion between Numeral Systems
3. Representation of Numbers
Positive and Negative Integer Numbers
Floating-Point Numbers
4. Text Representation
2

3. Numeral Systems
Conversion between Numeral Systems

4. Decimal numbers (base 10)
Represented using 10 numerals:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Each position represents a power of 10:
401 = 4*102 + 0*101 + 1*100 = 400 + 1
130 = 1*102 + 3*101 + 0*100 = 100 + 30
9786 = 9*103 + 7*102 + 8*101 + 6*100 =
= 9*1000 + 7*100 + 8*10 + 6*1
Decimal Numbers
4

5. Binary Numeral System
5
1 0 1 1 0 0 1 01 0 0 1 0 0 1 01 0 0 1 0 0 1 11 1 1 1 1 1 1 1
Binary numbers are represented by sequence
of bits (smallest unit of information – 0 or 1)
 Bits are easy to represent in electronics

6. Binary numbers (base 2)
Represented by 2 numerals: 0 and 1
Each position represents a power of 2:
 101b = 1*22 + 0*21 + 1*20 = 100b + 1b = 4 + 1 =
= 5
 110b = 1*22 + 1*21 + 0*20 = 100b + 10b = 4 + 2 =
= 6
 110101b = 1*25 + 1*24 + 0*23 + 1*22 + 0*21 + 1*20 =
= 32 + 16 + 4 + 1 =
= 53
Binary Numbers
6

7. Binary to Decimal Conversion
Multiply each numeral by its exponent:
 1001b = 1*23 + 1*20 = 1*8 + 1*1 =
= 9
 0111b = 0*23 + 1*22 + 1*21 + 1*20 =
= 100b + 10b + 1b = 4 + 2 + 1 =
= 7
 110110b = 1*25 + 1*24 + 0*23 + 1*22 + 1*21 =
= 100000b + 10000b + 100b + 10b =
= 32 + 16 + 4 + 2 =
= 54
7

8. Decimal to Binary Conversion
Divide by 2 and append the reminders in
reversed order:
500/2 = 250 (0)
250/2 = 125 (0)
125/2 = 62 (1)
62/2 = 31 (0) 500d = 111110100b
31/2 = 15 (1)
15/2 = 7 (1)
7/2 = 3 (1)
3/2 = 1 (1)
1/2 = 0 (1)
8

9. Hexadecimal Numbers
Hexadecimal numbers (base 16)
 Represented using 16 numerals:
0, 1, 2, ... 9, A, B, C, D, E and F
Usually prefixed with 0x
0  0x0 8  0x8
1  0x1 9  0x9
2  0x2 10  0xA
3  0x3 11  0xB
4  0x4 12  0xC
5  0x5 13  0xD
6  0x6 14  0xE
7  0x7 15  0xF
9

10. Hexadecimal Numbers (2)
Each position represents a power of 16:
 9786hex = 9*163 + 7*162 + 8*161 + 6*160 =
= 9*4096 + 7*256 + 8*16 + 6*1 =
= 38790
 0xABCDEFhex = 10*165 + 11*164 + 12*163 +
13*162 + 14*161 + 15*160 =
= 11259375
10

11. Hexadecimal to Decimal
Conversion
Multiply each digit by its exponent
 1F4hex = 1*162 + 15*161 + 4*160 =
= 1*256 + 15*16 + 4*1 =
= 500d
 FFhex = 15*161 + 15*160 =
= 240 + 15 =
= 255d
11

12. Decimal to Hexadecimal
Conversion
Divide by 16 and append the reminders in
reversed order
500/16 = 31 (4)
31/16 = 1 (F) 500d = 1F4hex
1/16 = 0 (1)
12

13. Binary to Hexadecimal
(and Back) Conversion
The conversion from binary to hexadecimal
(and back) is straightforward: each hex digit
corresponds to a sequence of 4 binary digits:
0x0 = 0000 0x8 = 1000
0x1 = 0001 0x9 = 1001
0x2 = 0010 0xA = 1010
0x3 = 0011 0xB = 1011
0x4 = 0100 0xC = 1100
0x5 = 0101 0xD = 1101
0x6 = 0110 0xE = 1110
0x7 = 0111 0xF = 1111
13

14. Numbers Representation
Positive and Negative Integers and
Floating-Point Numbers

15. Representation of Integers
A short is represented by 16 bits
100 = 26 + 25 + 22 =
= 00000000 01100100
An int is represented by 32 bits
65545 = 216 + 23 + 20 =
= 00000000 00000001 00000000 00001001
A char is represented by 16 bits
‘0’ = 48 = 25 + 24 =
= 00000000 00110000
15

16. Positive and Negative Numbers
A number's sign is determined by the
Most Significant Bit (MSB)
Only in signed integers: sbyte, short, int, long
Leading 0 means positive number
 Leading 1 means negative number
Example: (8 bit numbers)
0XXXXXXXb > 0 e.g. 00010010b = 18
00000000b = 0
1XXXXXXXb < 0 e.g. 10010010b = -110
16

17. Positive and Negative Numbers (2)
The largest positive 8-bit sbyte number is:
127 (27 - 1) = 01111111b
The smallest negative 8-bit number is:
-128 (-27) = 10000000b
The largest positive 32-bit int number is:
2 147 483 647 (231 - 1) = 01111…11111b
The smallest negative 32-bit number is:
-2 147 483 648 (-231) = 10000…00000b
17

18. Representation of 8-bit Numbers
+127 = 01111111
...
+3 = 00000011
+2 = 00000010
+1 = 00000001
+0 = 00000000
-1 = 11111111
-2 = 11111110
-3 = 11111101
...
-127 = 10000001
-128 = 10000000
Positive 8-bit numbers have the
format 0XXXXXXX
Their value is the decimal of
their last 7 bits (XXXXXXX)
Negative 8-bit numbers have
the format 1YYYYYYY
Their value is 128 (27) minus (-)
the decimal of YYYYYYY
10010010b = 27 – 10010b =
= 128 - 18 = -110
18

19. Floating-Point Numbers
Floating-point numbers representation
(according to the IEEE 754 standard*):
Example:
19
2k-1 20 2-1 2-2 2-n
S P0 ... Pk-1 M0 M1 ... Mn-1
Sign Exponent Mantissa
1 10000011 01010010100000000000000
Mantissa = 1,322265625Exponent = 4Sign = -1
Bits [22…0]Bits [30…23]Bit 31
* See http://en.wikipedia.org/wiki/Floating_point

20. Text Representation in
Computer Systems

21. How Computers Represent
Text Data?
A text encoding is a system that uses binary
numbers (1 and 0) to represent characters
 Letters, numerals, etc.
In the ASCII encoding each character consists
of 8 bits (one byte) of data
ASCII is used in nearly all personal computers
In the Unicode encoding each character
consists of 16 bits (two bytes) of data
Can represent many alphabets
21

22. Character Codes – ASCIITable
Excerpt
from the
ASCII
table
Binary
Code
Decimal
Code
Character
01000001 65 A
01000010 66 B
01000011 67 C
01000100 68 D
00100011 35 #
01100000 48 0
00110001 49 1
01111110 126 ~
22

23. Strings of Characters
Strings are sequences of characters
Null-terminated (like in C)
Represented by array
Characters in the strings can be:
8 bit (ASCII / windows-1251 / …)
16 bit (UTF-16)
… … … … … … … … 0
4 bytes
length … … … … … …
23

24. Questions?
Numeral Systems
http://academy.telerik.com

25. Exercises
1. Write a program to convert decimal numbers to their
binary representation.
2. Write a program to convert binary numbers to their
decimal representation.
3. Write a program to convert decimal numbers to their
hexadecimal representation.
4. Write a program to convert hexadecimal numbers to
their decimal representation.
5. Write a program to convert hexadecimal numbers to
binary numbers (directly).
6. Write a program to convert binary numbers to
hexadecimal numbers (directly).
25

26. Exercises (2)
7. Write a program to convert from any numeral system
of given base s to any other numeral system of base
d (2 ≤ s, d ≤ 16).
8. Write a program that shows the binary
representation of given 16-bit signed integer number
(the C# type short).
9. * Write a program that shows the internal binary
representation of given 32-bit signed floating-point
number in IEEE 754 format (the C# type float).
Example: -27,25  sign = 1, exponent = 10000011,
mantissa = 10110100000000000000000.
26