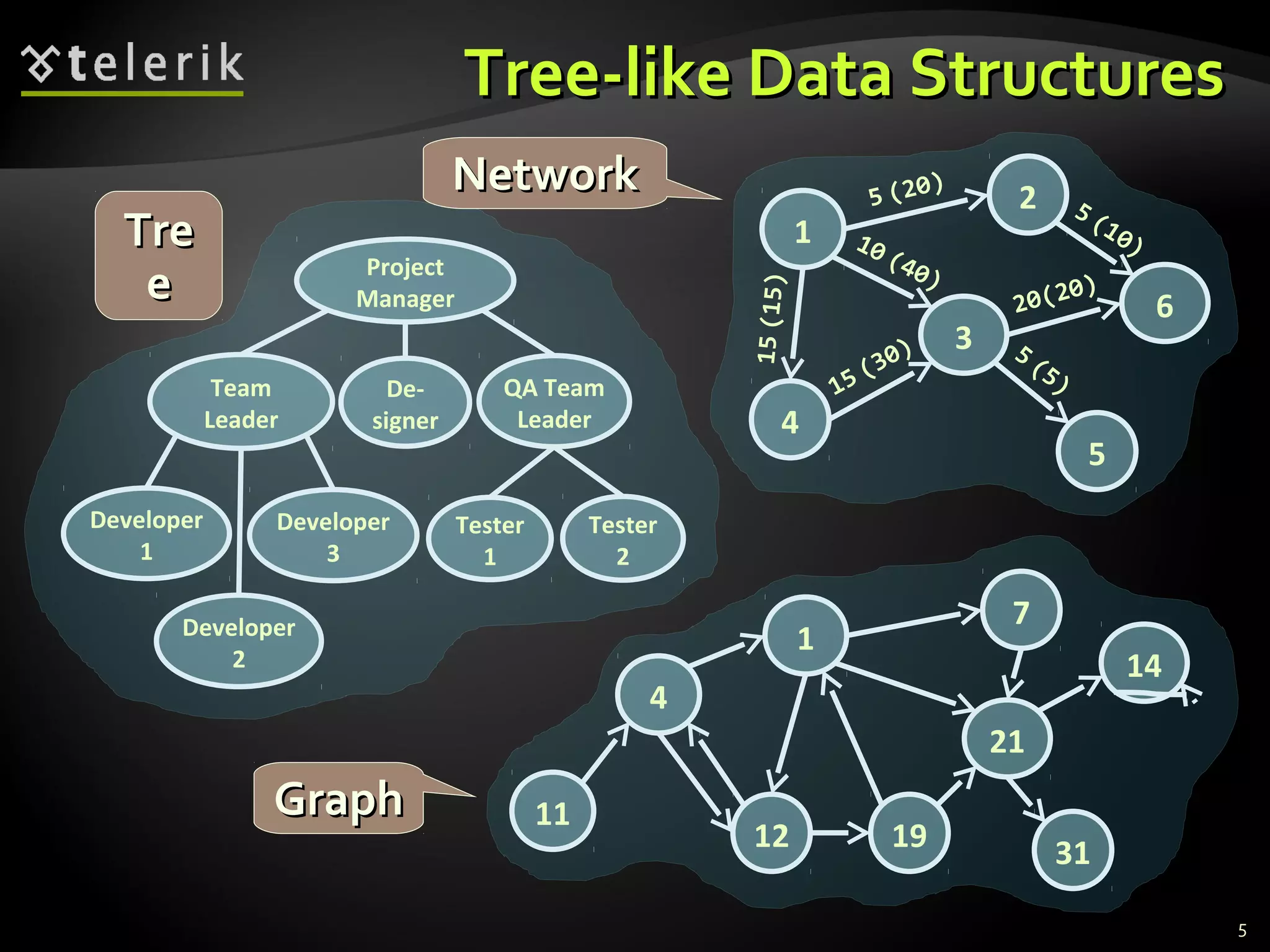
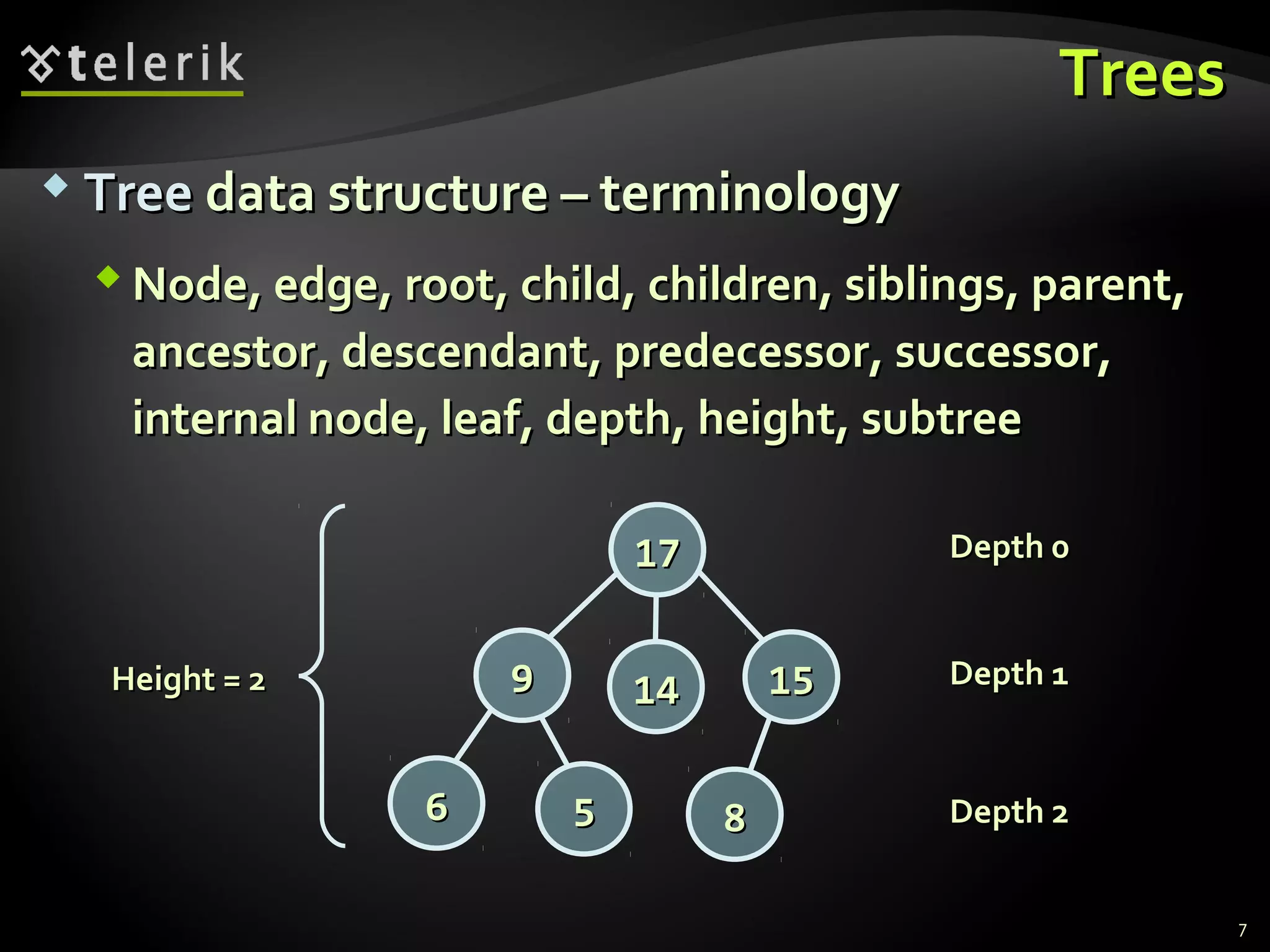
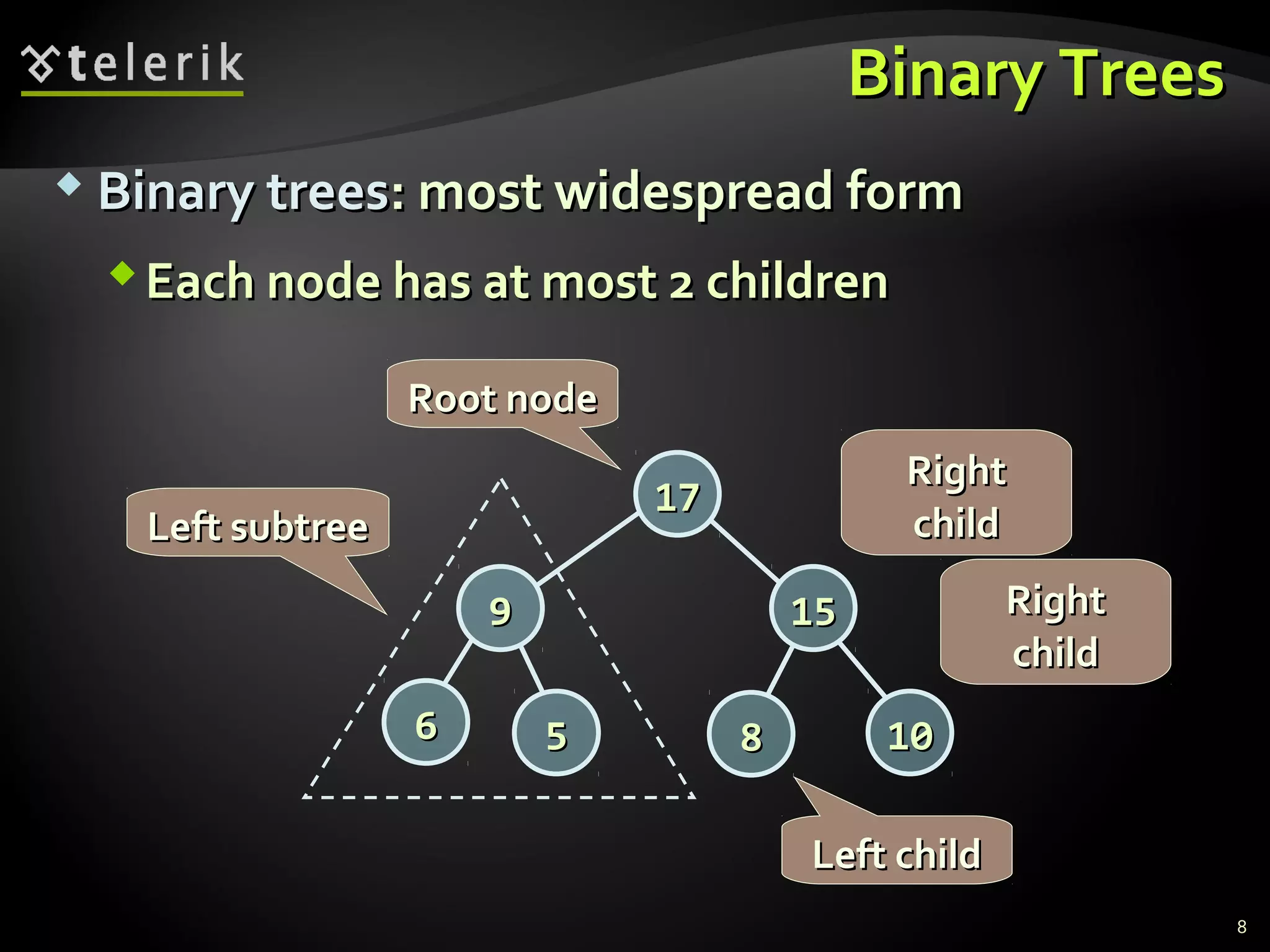
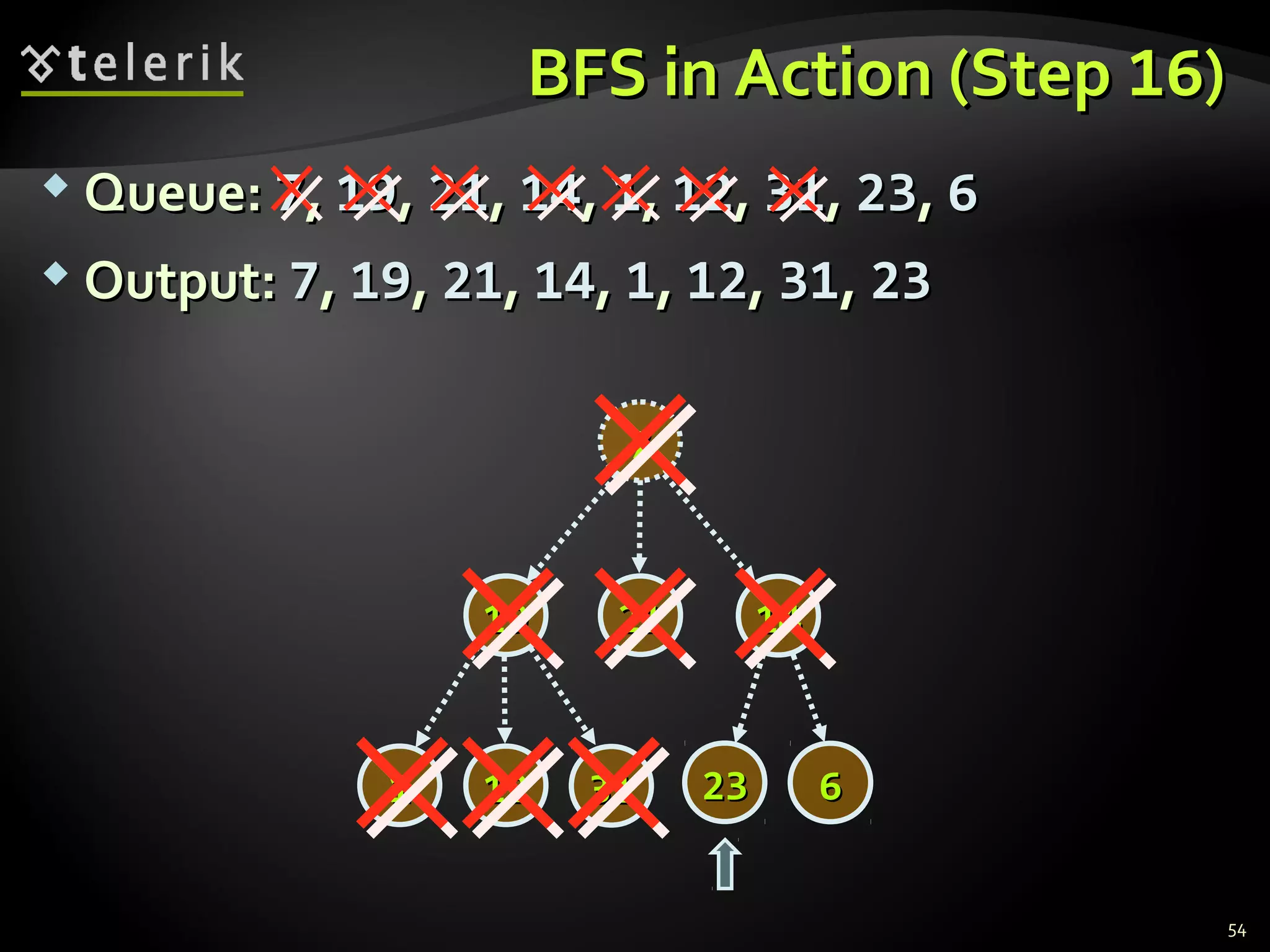
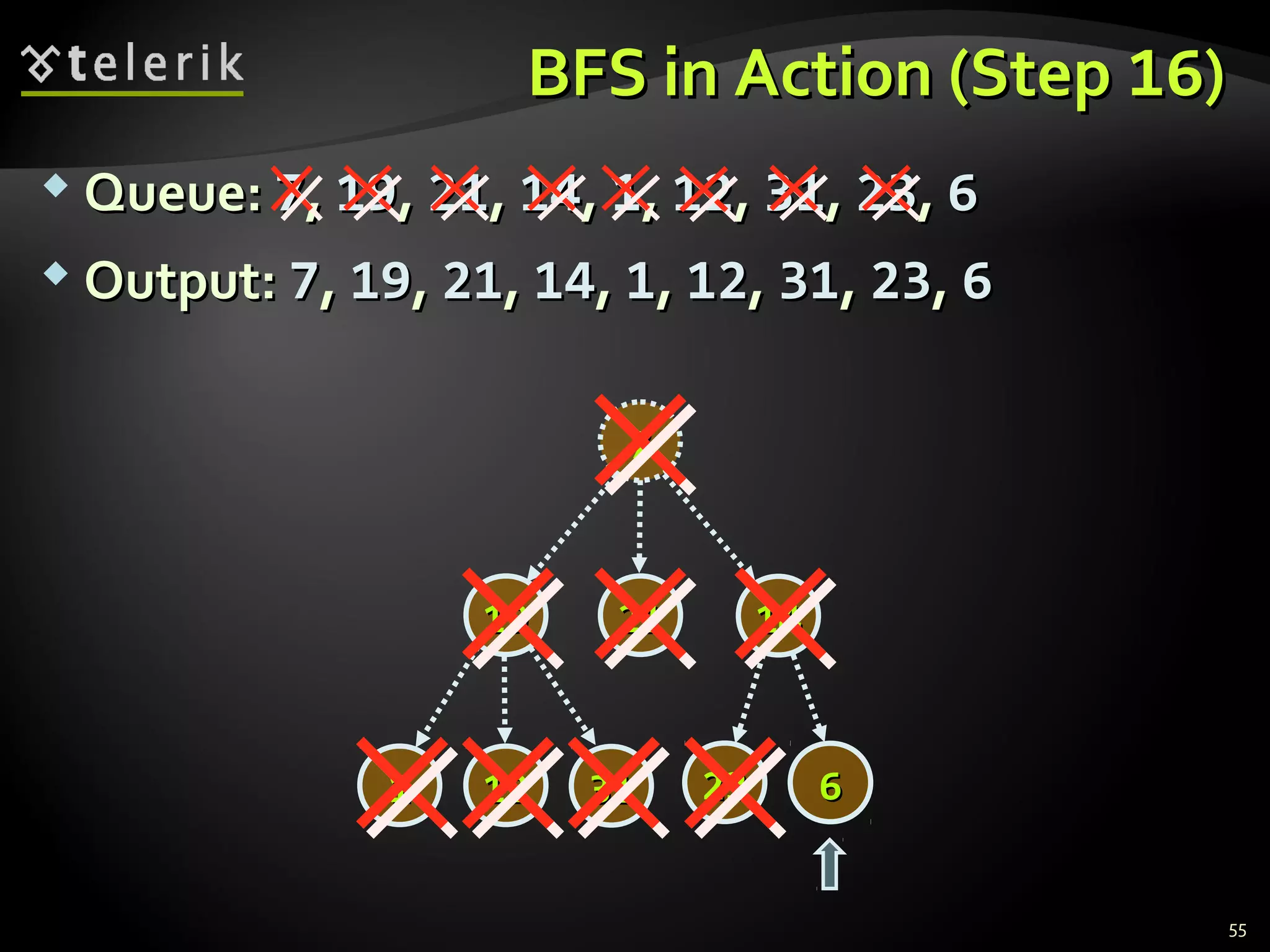
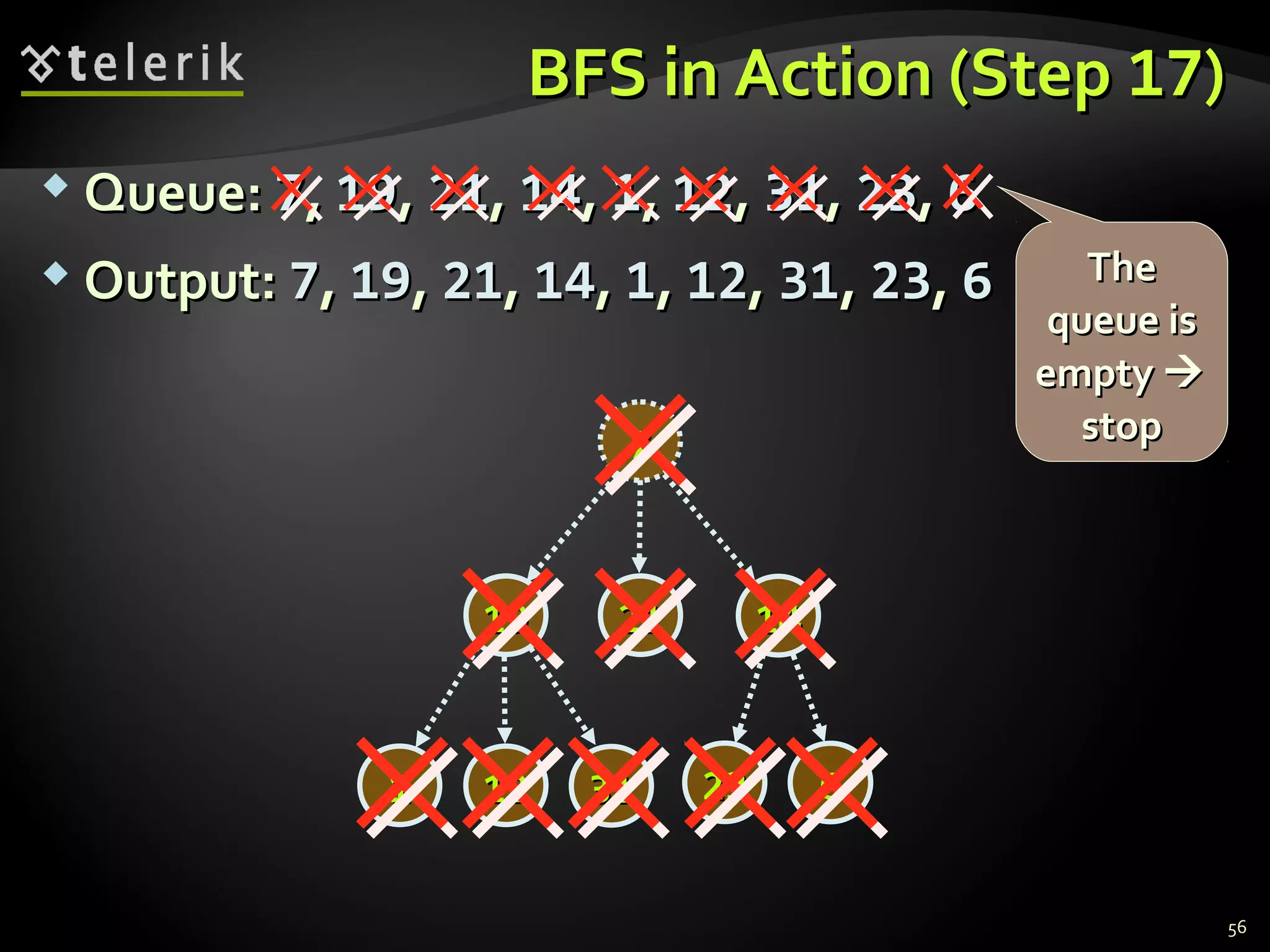
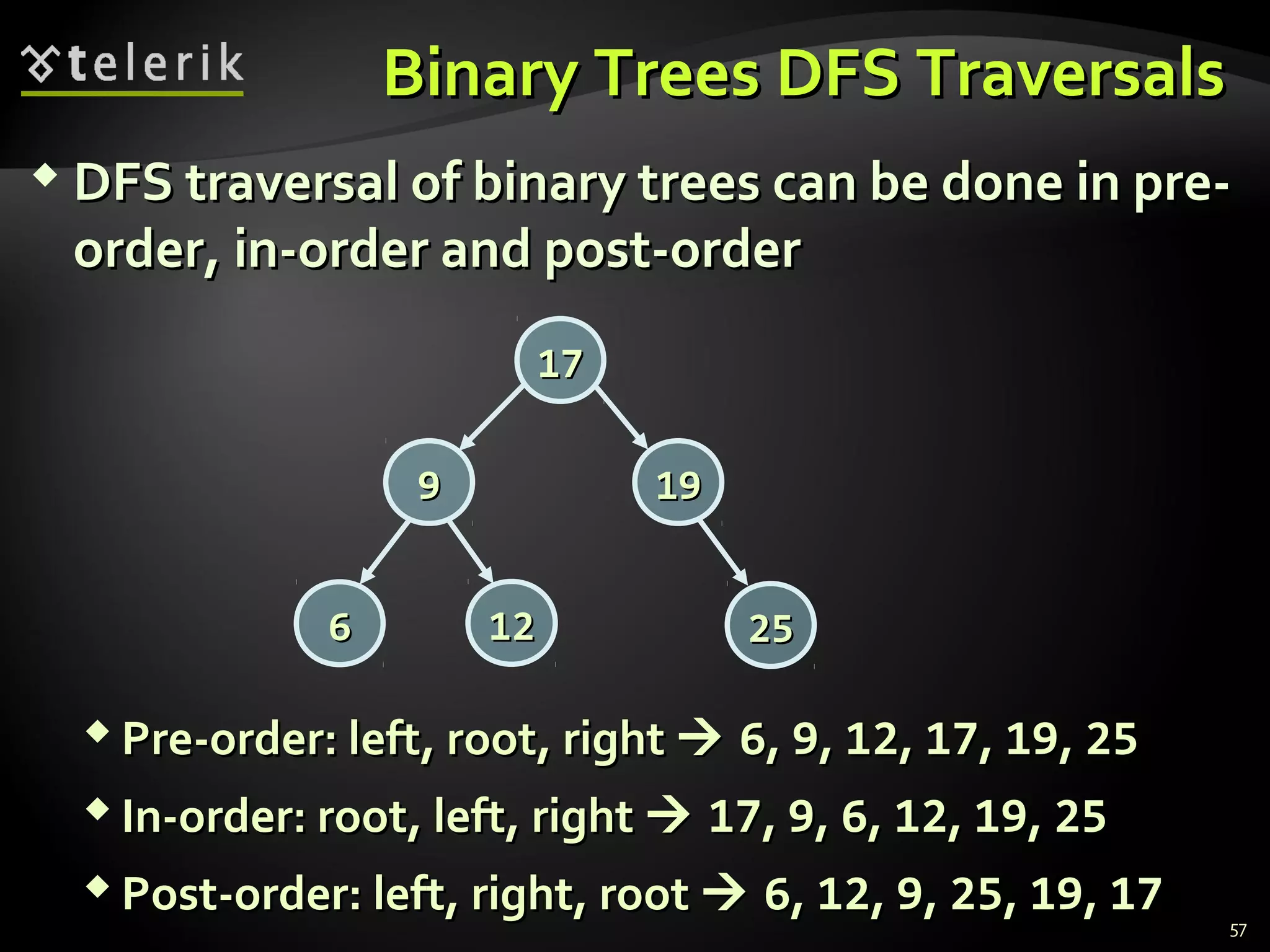
This document discusses trees and graphs as tree-like data structures. It defines key terminology used for trees like nodes, edges, roots, and leaves. It also describes different types of trees like binary search trees and balanced trees. The document provides examples of implementing tree data structures recursively using class definitions. It explains algorithms for traversing trees, specifically depth-first search (DFS) and breadth-first search (BFS). DFS is demonstrated step-by-step on a sample tree. The document also briefly mentions graphs as another tree-like structure.

1. Trees and GraphsTrees and Graphs
Trees, Binary SearchTrees, BalancedTrees, GraphsTrees, Binary SearchTrees, BalancedTrees, Graphs
Svetlin NakovSvetlin Nakov
Telerik CorporationTelerik Corporation
www.telerik.comwww.telerik.com

2. Table of ContentsTable of Contents
1.1. Tree-like Data StructuresTree-like Data Structures
2.2. Trees and Related TerminologyTrees and Related Terminology
3.3. Implementing TreesImplementing Trees
4.4. Traversing TreesTraversing Trees
5.5. Balanced TreesBalanced Trees
6.6. GraphsGraphs
2

3. Tree-like Data StructuresTree-like Data Structures
Trees, BalancedTrees, Graphs, NetworksTrees, BalancedTrees, Graphs, Networks

4. Tree-like Data StructuresTree-like Data Structures
 Tree-like data structures areTree-like data structures are
Branched recursive data structuresBranched recursive data structures
 Consisting of nodesConsisting of nodes
 Each node can be connected to other nodesEach node can be connected to other nodes
 Examples of tree-like structuresExamples of tree-like structures
Trees: binary / other degree, balanced, etc.Trees: binary / other degree, balanced, etc.
Graphs: directed / undirected, weighted, etc.Graphs: directed / undirected, weighted, etc.
NetworksNetworks
4

5. Tree-like Data StructuresTree-like Data Structures
5
Project
Manager
Team
Leader
De-
signer
QA Team
Leader
Developer
1
Developer
2
Tester
1
Developer
3
Tester
2
TreTre
ee
GraphGraph
2
3
6
1
4
5
7
19
21
14
1
12 31
4
11
5 (20)
5 (10)
15(15)
15 (30) 5 (5)
20(20)
10 (40)
NetworkNetwork

6. Trees and RelatedTrees and Related
TerminologyTerminology
Node, Edge, Root, Children, Parent, Leaf ,Node, Edge, Root, Children, Parent, Leaf ,
Binary SearchTree, BalancedTreeBinary SearchTree, BalancedTree

7. TreesTrees
 TreeTree data structure – terminologydata structure – terminology
 Node, edge, root, child, children, siblings, parent,Node, edge, root, child, children, siblings, parent,
ancestor, descendant, predecessor, successor,ancestor, descendant, predecessor, successor,
internal node, leaf, depth, height, subtreeinternal node, leaf, depth, height, subtree
Height = 2Height = 2
Depth 0Depth 0
Depth 1Depth 1
Depth 2Depth 2
1717
1515141499
66 55 88
7

8. Binary TreesBinary Trees
 Binary treesBinary trees: most widespread form: most widespread form
Each node has at most 2 childrenEach node has at most 2 children
1010
1717
151599
66 55 88
Root nodeRoot node
Left subtreeLeft subtree
RightRight
childchild
RightRight
childchild
Left childLeft child
8

9. Binary Search TreesBinary Search Trees
 Binary search treesBinary search trees areare orderedordered
For each nodeFor each node xx in the treein the tree
 All the elements of the left subtree ofAll the elements of the left subtree of xx areare ≤≤ xx
 All the elements of the right subtree ofAll the elements of the right subtree of xx areare >> xx
 Binary search trees can beBinary search trees can be balancedbalanced
Balanced treesBalanced trees have height ofhave height of ~ log~ log22((xx))
Balanced trees have for each node nearly equalBalanced trees have for each node nearly equal
number of nodes in its subtreesnumber of nodes in its subtrees
9

10. Binary Search Trees (2)Binary Search Trees (2)
 Example of balanced binary search treeExample of balanced binary search tree
 If the tree is balanced, add / search / deleteIf the tree is balanced, add / search / delete
operations take approximatelyoperations take approximately log(log(nn)) stepssteps
1717
191999
66 1212 2525
10

11. ImplementingTreesImplementingTrees
RecursiveTree Data StructureRecursiveTree Data Structure

12. Recursive Tree DefinitionRecursive Tree Definition
 The recursive definition forThe recursive definition for treetree data structure:data structure:
A single node is treeA single node is tree
Tree nodes can have zero or multiple childrenTree nodes can have zero or multiple children
that are also treesthat are also trees
 Tree node definition in C#Tree node definition in C#
12
public class TreeNode<T>public class TreeNode<T>
{{
private T value;private T value;
private List<TreeNode<T>> children;private List<TreeNode<T>> children;
……
}}
The valueThe value
contained in thecontained in the
nodenode
List of child nodes,List of child nodes,
which are of the samewhich are of the same
typetype

13. TreeNode<int>TreeNode<int> StructureStructure
13
77 childrenchildren
1919 childrenchildren 2121 childrenchildren 1414 childrenchildren
TreeNode<int>TreeNode<int>
11 childrenchildren
1212 childrenchildren
3131 childrenchildren 2323 childrenchildren 66 childrenchildren
int valueint value
List<TreeNode<int>>List<TreeNode<int>>
childrenchildren

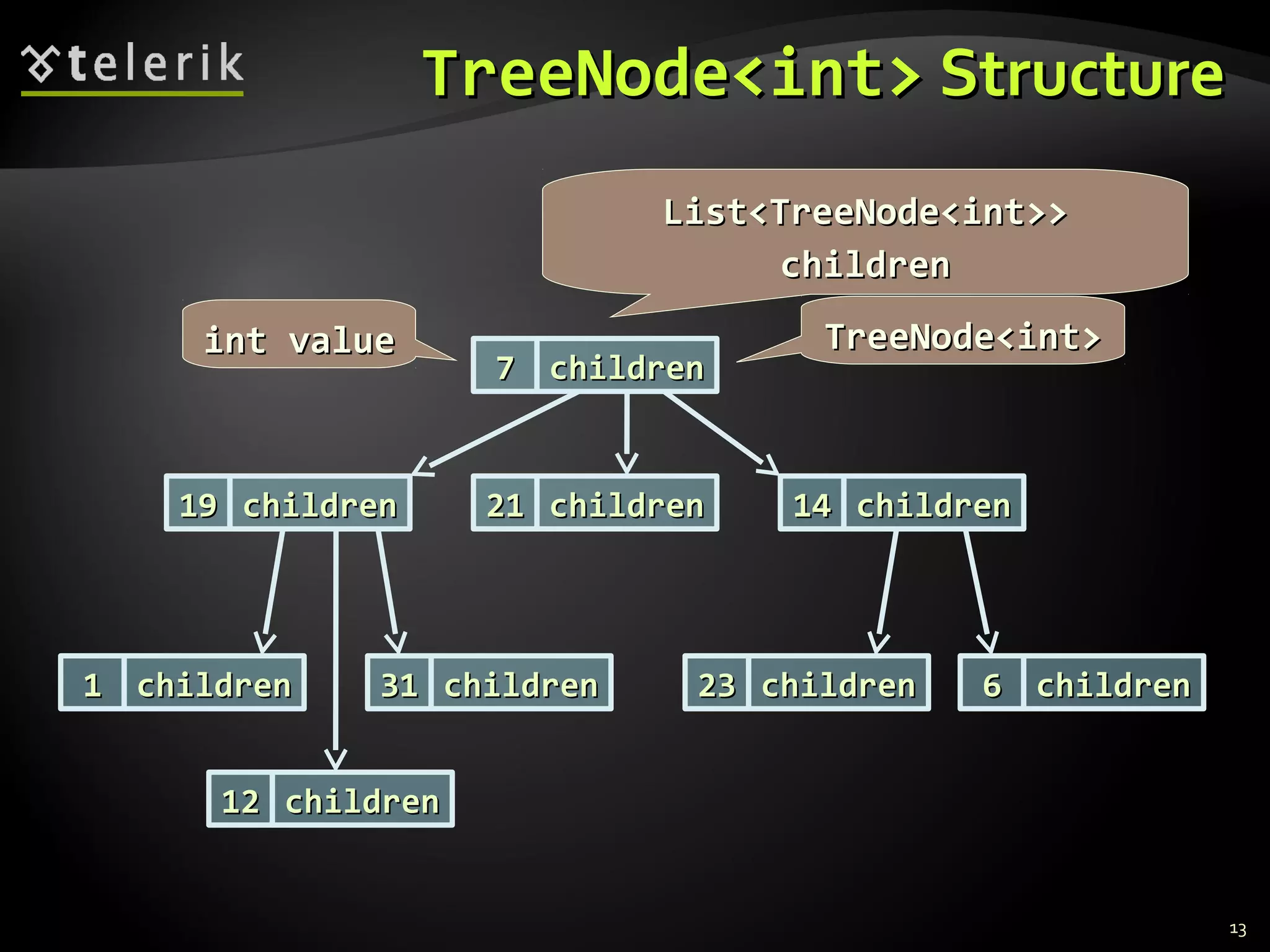
14. ImplementingImplementing TreeNodeTreeNode<T><T>
14
public TreeNode(T value)public TreeNode(T value)
{{
this.value = value;this.value = value;
this.children = new List<TreeNode<T>>();this.children = new List<TreeNode<T>>();
}}
public T Valuepublic T Value
{{
get { return this.value; }get { return this.value; }
set { this.value = value; }set { this.value = value; }
}}
public void AddChild(TreeNode<T> child)public void AddChild(TreeNode<T> child)
{{
child.hasParent = true;child.hasParent = true;
this.children.Add(child);this.children.Add(child);
}}
public TreeNode<T> GetChild(int index)public TreeNode<T> GetChild(int index)
{{
return this.children[index];return this.children[index];
}}

15.  The classThe class Tree<T>Tree<T> keeps tree's root nodekeeps tree's root node
ImplementingImplementing Tree<T>Tree<T>
15
public class Tree<T>public class Tree<T>
{{
private TreeNode<T> root;private TreeNode<T> root;
public Tree(T value, params Tree<T>[] children): this(value)public Tree(T value, params Tree<T>[] children): this(value)
{{
foreach (Tree<T> child in children)foreach (Tree<T> child in children)
{{
this.root.AddChild(child.root);this.root.AddChild(child.root);
}}
}}
public TreeNode<T> Rootpublic TreeNode<T> Root
{{
get { return this.root; }get { return this.root; }
}}
}}
Flexible constructorFlexible constructor
for building treesfor building trees

16. Building a TreeBuilding a Tree
16
Tree<int> tree =Tree<int> tree =
new Tree<int>(7,new Tree<int>(7,
new Tree<int>(19,new Tree<int>(19,
new Tree<int>(1),new Tree<int>(1),
new Tree<int>(12),new Tree<int>(12),
new Tree<int>(31)),new Tree<int>(31)),
new Tree<int>(21),new Tree<int>(21),
new Tree<int>(14,new Tree<int>(14,
new Tree<int>(23),new Tree<int>(23),
new Tree<int>(6))new Tree<int>(6))
););
77
14141919
2323 66
2121
313111 1212
 Constructing tree by nested constructors:Constructing tree by nested constructors:

17. TreeTraversalsTreeTraversals
DFS and BFSTraversalsDFS and BFSTraversals

18. Tree Traversal AlgorithmsTree Traversal Algorithms
 Traversing a treeTraversing a tree means to visit each of itsmeans to visit each of its
nodes exactly one in particular ordernodes exactly one in particular order
Many traversal algorithms are knownMany traversal algorithms are known
Depth-First Search (DFS)Depth-First Search (DFS)
 Visit node's successors firstVisit node's successors first
 Usually implemented by recursionUsually implemented by recursion
Breadth-First Search (BFS)Breadth-First Search (BFS)
 Nearest nodes visited firstNearest nodes visited first
 Implemented by a queueImplemented by a queue
18

19.  Depth-First SearchDepth-First Search first visits all descendantsfirst visits all descendants
of given node recursively, finally visits theof given node recursively, finally visits the
node itselfnode itself
 DFS algorithm pseudo codeDFS algorithm pseudo code
Depth-First Search (DFS)Depth-First Search (DFS)
DFS(node)DFS(node)
{{
for each childfor each child cc of nodeof node
DFS(DFS(cc););
print the current node;print the current node;
}}
77
14141919
2323 66
2121
313111 1212
1 2 3
4 5 8
6 7
9
19

20. DFS in Action (StepDFS in Action (Step 11))
 Stack:Stack: 77
 Output:Output: (empty)(empty)
20
77
14141919
2323 66
2121
313111 1212

21. DFS in Action (StepDFS in Action (Step 22))
 Stack:Stack: 77,, 1919
 Output:Output: (empty)(empty)
21
77
14141919
2323 66
2121
313111 1212

22. DFS in Action (StepDFS in Action (Step 33))
 Stack:Stack: 77,, 1919,, 11
 Output:Output: (empty)(empty)
22
77
14141919
2323 66
2121
313111 1212

23. DFS in Action (StepDFS in Action (Step 44))
 Stack:Stack: 77,, 1919
 Output:Output: 11
23
77
14141919
2323 66
2121
313111 1212

24. DFS in Action (StepDFS in Action (Step 55))
 Stack:Stack: 77,, 1919,, 1212
 Output:Output: 11
24
77
14141919
2323 66
2121
313111 1212

25. DFS in Action (StepDFS in Action (Step 66))
 Stack:Stack: 77,, 1919
 Output:Output: 11,, 1212
25
77
14141919
2323 66
2121
313111 1212

26. DFS in Action (StepDFS in Action (Step 77))
 Stack:Stack: 77,, 1919,, 3131
 Output:Output: 11,, 1212
26
77
14141919
2323 66
2121
313111 1212

27. DFS in Action (StepDFS in Action (Step 88))
 Stack:Stack: 77,, 1919
 Output:Output: 11,, 1212,, 3131
27
77
14141919
2323 66
2121
313111 1212

28. DFS in Action (StepDFS in Action (Step 99))
 Stack:Stack: 77
 Output:Output: 11,, 1212,, 3131,, 1919
28
77
14141919
2323 66
2121
313111 1212

29. DFS in Action (StepDFS in Action (Step 1010))
 Stack:Stack: 77,, 2121
 Output:Output: 11,, 1212,, 3131,, 1919
29
77
14141919
2323 66
2121
313111 1212

30. DFS in Action (StepDFS in Action (Step 1111))
 Stack:Stack: 77
 Output:Output: 11,, 1212,, 3131,, 1919,, 2121
30
77
14141919
2323 66
2121
313111 1212

31. DFS in Action (StepDFS in Action (Step 1212))
 Stack:Stack: 77,, 1414
 Output:Output: 11,, 1212,, 3131,, 1919,, 2121
31
77
14141919
2323 66
2121
313111 1212

32. DFS in Action (StepDFS in Action (Step 1313))
 Stack:Stack: 77,, 1414,, 2323
 Output:Output: 11,, 1212,, 3131,, 1919,, 2121
32
77
14141919
2323 66
2121
313111 1212

33. DFS in Action (StepDFS in Action (Step 1414))
 Stack:Stack: 77,, 1414
 Output:Output: 11,, 1212,, 3131,, 1919,, 2121,, 2323
33
77
14141919
2323 66
2121
313111 1212

34. DFS in Action (StepDFS in Action (Step 1515))
 Stack:Stack: 77,, 1414,, 66
 Output:Output: 11,, 1212,, 3131,, 1919,, 2121,, 2323
34
77
14141919
2323 66
2121
313111 1212

35. DFS in Action (StepDFS in Action (Step 1616))
 Stack:Stack: 77,, 1414
 Output:Output: 11,, 1212,, 3131,, 1919,, 2121,, 2323,, 66
35
77
14141919
2323 66
2121
313111 1212

36. DFS in Action (StepDFS in Action (Step 1717))
 Stack:Stack: 77
 Output:Output: 11,, 1212,, 3131,, 1919,, 2121,, 2323,, 66,, 1414
36
77
14141919
2323 66
2121
313111 1212

37. DFS in Action (StepDFS in Action (Step 1818))
 Stack:Stack: (empty)(empty)
 Output:Output: 11,, 1212,, 3131,, 1919,, 2121,, 2323,, 66,, 1414,, 77
37
77
14141919
2323 66
2121
313111 1212
TraversalTraversal
finishedfinished

38.  Breadth-First SearchBreadth-First Search first visits the neighborfirst visits the neighbor
nodes, later their neighbors, etc.nodes, later their neighbors, etc.
 BFS algorithm pseudo codeBFS algorithm pseudo code
Breadth-First Search (BFS)Breadth-First Search (BFS)
BFS(node)BFS(node)
{{
queuequeue  nodenode
while queue not emptywhile queue not empty
vv  queuequeue
print vprint v
for each childfor each child cc ofof vv
queuequeue  cc
}}
77
14141919
2323 66
2121
313111 1212
5 6 7
2 3 4
8 9
1
38

39. BFS in Action (StepBFS in Action (Step 11))
 Queue:Queue: 77
 Output:Output: 77
39
77
14141919
2323 66
2121
313111 1212

40. BFS in Action (StepBFS in Action (Step 22))
 Queue:Queue: 77,, 1919
 Output:Output: 77
40
77
14141919
2323 66
2121
313111 1212

41. BFS in Action (StepBFS in Action (Step 33))
 Queue:Queue: 77,, 1919,, 2121
 Output:Output: 77
41
77
14141919
2323 66
2121
313111 1212

42. BFS in Action (StepBFS in Action (Step 44))
 Queue:Queue: 77,, 1919,, 2121,, 1414
 Output:Output: 77
42
77
14141919
2323 66
2121
313111 1212

43. BFS in Action (StepBFS in Action (Step 55))
 Queue:Queue: 77,, 1919,, 2121,, 1414
 Output:Output: 77,, 1919
43
77
14141919
2323 66
2121
313111 1212

44. BFS in Action (StepBFS in Action (Step 66))
 Queue:Queue: 77,, 1919,, 2121,, 1414,, 11
 Output:Output: 77,, 1919
44
77
14141919
2323 66
2121
313111 1212

45. BFS in Action (StepBFS in Action (Step 77))
 Queue:Queue: 77,, 1919,, 2121,, 1414,, 11,, 1212
 Output:Output: 77,, 1919
45
77
14141919
2323 66
2121
313111 1212

46. BFS in Action (StepBFS in Action (Step 88))
 Queue:Queue: 77,, 1919,, 2121,, 1414,, 11,, 1212,, 3131
 Output:Output: 77,, 1919
46
77
14141919
2323 66
2121
313111 1212

47. BFS in Action (StepBFS in Action (Step 99))
 Queue:Queue: 77,, 1919,, 2121,, 1414,, 11,, 1212,, 3131
 Output:Output: 77,, 1919,, 2121
47
77
14141919
2323 66
2121
313111 1212

48. BFS in Action (StepBFS in Action (Step 1010))
 Queue:Queue: 77,, 1919,, 2121,, 1414,, 11,, 1212,, 3131
 Output:Output: 77,, 1919,, 2121,, 1414
48
77
14141919
2323 66
2121
313111 1212

49. BFS in Action (StepBFS in Action (Step 1111))
 Queue:Queue: 77,, 1919,, 2121,, 1414,, 11,, 1212,, 3131,, 2323
 Output:Output: 77,, 1919,, 2121,, 1414
49
77
14141919
2323 66
2121
313111 1212

50. BFS in Action (StepBFS in Action (Step 1212))
 Queue:Queue: 77,, 1919,, 2121,, 1414,, 11,, 1212,, 3131,, 2323,, 66
 Output:Output: 77,, 1919,, 2121,, 1414
50
77
14141919
2323 66
2121
313111 1212

51. BFS in Action (StepBFS in Action (Step 1313))
 Queue:Queue: 77,, 1919,, 2121,, 1414,, 11,, 1212,, 3131,, 2323,, 66
 Output:Output: 77,, 1919,, 2121,, 1414,, 11
51
77
14141919
2323 66
2121
313111 1212

52. BFS in Action (StepBFS in Action (Step 1414))
 Queue:Queue: 77,, 1919,, 2121,, 1414,, 11,, 1212,, 3131,, 2323,, 66
 Output:Output: 77,, 1919,, 2121,, 1414,, 11,, 1122
52
77
14141919
2323 66
2121
313111 1212

53. BFS in Action (StepBFS in Action (Step 1515))
 Queue:Queue: 77,, 1919,, 2121,, 1414,, 11,, 1212,, 3131,, 2323,, 66
 Output:Output: 77,, 1919,, 2121,, 1414,, 11,, 1122,, 3131
53
77
14141919
2323 66
2121
313111 1212

54. BFS in Action (StepBFS in Action (Step 1616))
 Queue:Queue: 77,, 1919,, 2121,, 1414,, 11,, 1212,, 3131,, 2323,, 66
 Output:Output: 77,, 1919,, 2121,, 1414,, 11,, 1122,, 3131,, 2323
54
77
14141919
2323 66
2121
313111 1212

55. BFS in Action (StepBFS in Action (Step 1616))
 Queue:Queue: 77,, 1919,, 2121,, 1414,, 11,, 1212,, 3131,, 2323,, 66
 Output:Output: 77,, 1919,, 2121,, 1414,, 11,, 1122,, 3131,, 2323,, 66
55
77
14141919
2323 66
2121
313111 1212

56. BFS in Action (StepBFS in Action (Step 1717))
 Queue:Queue: 77,, 1919,, 2121,, 1414,, 11,, 1212,, 3131,, 2323,, 66
 Output:Output: 77,, 1919,, 2121,, 1414,, 11,, 1122,, 3131,, 2323,, 66
56
77
14141919
2323 66
2121
313111 1212
TheThe
queue isqueue is
emptyempty 
stopstop

57. Binary TreesBinary Trees DFS TraversalsDFS Traversals
 DFS traversal of binary trees can be done in pre-DFS traversal of binary trees can be done in pre-
order, in-order and post-orderorder, in-order and post-order
 Pre-order: left, root, rightPre-order: left, root, right  66,, 99,, 1212,, 1717,, 1919,, 2525
 In-order: root, left, rightIn-order: root, left, right  1717,, 99,, 66,, 1212,, 1919,, 2525
 Post-order: left, right, rootPost-order: left, right, root  66,, 1212,, 99,, 2525,, 1919,, 1717
1717
191999
66 1212 2525
57

58. Iterative DFS and BFSIterative DFS and BFS
 What will happen if in the Breadth-First SearchWhat will happen if in the Breadth-First Search
(BFS) algorithm a stack is used instead of queue?(BFS) algorithm a stack is used instead of queue?
 An iterative Depth-First Search (DFS) – in-orderAn iterative Depth-First Search (DFS) – in-order
58
BFS(node)BFS(node)
{{
queuequeue  nodenode
while queue not emptywhile queue not empty
vv  queuequeue
print vprint v
for each childfor each child cc ofof vv
queuequeue  cc
}}
DFS(node)DFS(node)
{{
stackstack  nodenode
while stack not emptywhile stack not empty
vv  stackstack
print vprint v
for each childfor each child cc ofof vv
stackstack  cc
}}

59. Trees andTraversalsTrees andTraversals
Live DemoLive Demo

60. Balanced SearchTreesBalanced SearchTrees
AVLTrees, B-Trees, Red-BlackTrees, AA-TreesAVLTrees, B-Trees, Red-BlackTrees, AA-Trees

61. Balanced Binary Search TreesBalanced Binary Search Trees
 Ordered Binary Trees (Ordered Binary Trees (Binary Search TreesBinary Search Trees))
For each nodeFor each node xx the left subtree has valuesthe left subtree has values ≤ x≤ x
and the right subtree has valuesand the right subtree has values > x> x
 Balanced TreesBalanced Trees
For each node its subtrees contain nearly equalFor each node its subtrees contain nearly equal
number of nodesnumber of nodes  nearly the same heightnearly the same height
 Balanced Binary Search TreesBalanced Binary Search Trees
Ordered binary search trees that have height ofOrdered binary search trees that have height of
loglog22(n)(n) wherewhere nn is the number of their nodesis the number of their nodes
Searching costs aboutSearching costs about loglog22(n)(n) comparisonscomparisons
61

62. Balanced Binary Search Tree –Balanced Binary Search Tree –
ExampleExample
62
3333
1818
1515 2424
33 1717 2020 2929
5454
4242 6060
3737 4343 5959 8585

63. Balanced Binary Search TreesBalanced Binary Search Trees
 Balanced binary search trees are hard toBalanced binary search trees are hard to
implementimplement
 Rebalancing the tree after insert / delete is complexRebalancing the tree after insert / delete is complex
 Well known implementations of balanced binaryWell known implementations of balanced binary
search treessearch trees
 AVL trees – ideally balanced, very complexAVL trees – ideally balanced, very complex
 Red-black trees – roughly balanced, more simpleRed-black trees – roughly balanced, more simple
 AA-Trees – relatively simple to implementAA-Trees – relatively simple to implement
 Find / insert / delete operations needFind / insert / delete operations need loglog22(n)(n) stepssteps
63

64. B-TreesB-Trees
 B-treesB-trees are generalization of the concept ofare generalization of the concept of
ordered binary search treesordered binary search trees
B-tree of orderB-tree of order dd has betweenhas between dd andand 2*d2*d keys inkeys in
a node and betweena node and between d+1d+1 andand 2*d+12*d+1 child nodeschild nodes
The keys in each node are ordered increasinglyThe keys in each node are ordered increasingly
All keys in a child node have values betweenAll keys in a child node have values between
their left and right parent keystheir left and right parent keys
 If the b-tree is balanced, its search / insert / addIf the b-tree is balanced, its search / insert / add
operations take about log(n) stepsoperations take about log(n) steps
 B-trees can be efficiently stored on the diskB-trees can be efficiently stored on the disk
64

65.  B-Tree of orderB-Tree of order 22,, also known asalso known as 22--33--44-tree:-tree:
B-Tree – ExampleB-Tree – Example
65
1717 2121
77 1111 1818 2020 2626 3131
22 44 55 66 88 99 1212 1616 2222 2323 2525 2727 2929 3030 3232 3535

66. Balanced Trees in .NETBalanced Trees in .NET
 .NET Framework has several built-in.NET Framework has several built-in
implementations of balanced search trees:implementations of balanced search trees:
SortedDictionary<K,V>SortedDictionary<K,V>
 Red-black tree based map of key-value pairsRed-black tree based map of key-value pairs
OrderedSet<T>OrderedSet<T>
 Red-black tree based set of elementsRed-black tree based set of elements
 External libraries like "Wintellect PowerExternal libraries like "Wintellect Power
Collections for .NET" are more flexibleCollections for .NET" are more flexible
http://powercollections.codeplex.comhttp://powercollections.codeplex.com
66

67. GraphsGraphs
Definitions, Representation,Traversal AlgorithmsDefinitions, Representation,Traversal Algorithms

68. Graph Data StructureGraph Data Structure
 Set of nodes with many-to-many relationshipSet of nodes with many-to-many relationship
between them is calledbetween them is called graphgraph
 Each node hasEach node has multiplemultiple predecessorspredecessors
 Each node hasEach node has multiplemultiple successorssuccessors
77
1919
2121
1414
11
1212
3131
44
1111
Node with multipleNode with multiple
predecessorspredecessors
Node withNode with
multiplemultiple
successorssuccessors
68

69. Graph DefinitionsGraph Definitions
 NodeNode ((vertexvertex))
Element of graphElement of graph
Can have name or valueCan have name or value
Keeps a list of adjacent nodesKeeps a list of adjacent nodes
 EdgeEdge
Connection between two nodesConnection between two nodes
Can be directed / undirectedCan be directed / undirected
Can be weighted / unweightedCan be weighted / unweighted
Can have name / valueCan have name / value
AA
NodeNode
AA
EdgeEdge
BB
69

70. Graph Definitions (2)Graph Definitions (2)
 Directed graphDirected graph
 Edges have directionEdges have direction
 Undirected graphUndirected graph
 Undirected edgesUndirected edges
77
1919
2121
11
1212
44
33
2222
22
33
GG
JJ
FF
DD
AA
EE CC HH
70

71. Graph Definitions (3)Graph Definitions (3)
 Weighted graphWeighted graph
Weight (cost) is associated with each edgeWeight (cost) is associated with each edge
GG
JJ
FF
DD
AA
EE CC HH
QQ
KK
NN
10
4
14
6 16
9
8
7
5
22
3
71

72. Graph Definitions (4)Graph Definitions (4)
 PathPath (in undirected graph)(in undirected graph)
Sequence of nodes nSequence of nodes n11, n, n22, …, … nnkk
Edge exists between each pair of nodesEdge exists between each pair of nodes nnii,,nni+1i+1
Examples:Examples:
 A, B, CA, B, C is a pathis a path
 H, K, CH, K, C is not a pathis not a path
GG
CCBB
AA
HH NN
KK
72

73. Graph Definitions (5)Graph Definitions (5)
 PathPath (in directed graph)(in directed graph)
Sequence of nodes nSequence of nodes n11, n, n22, …, … nnkk
Directed edge exists between each pair ofDirected edge exists between each pair of
nodesnodes nnii,,nni+1i+1
Examples:Examples:
 A, B, CA, B, C is a pathis a path
 A, G, KA, G, K is not a pathis not a path GG
CCBB
AA
HH NN
KK
73

74. Graph Definitions (6)Graph Definitions (6)
 CycleCycle
Path that ends back at the starting nodePath that ends back at the starting node
Example:Example:
 A, B, C, G, AA, B, C, G, A
 Simple pathSimple path
 No cycles in pathNo cycles in path
 Acyclic graphAcyclic graph
 Graph with no cyclesGraph with no cycles
 Acyclic undirected graphs are treesAcyclic undirected graphs are trees
GG
CCBB
AA
HH NN
KK
74

75. UnconnectedUnconnected
graph with twograph with two
connectedconnected
componentscomponents
Graph Definitions (8)Graph Definitions (8)
 Two nodes areTwo nodes are reachablereachable ifif
Path exists between themPath exists between them
 Connected graphConnected graph
Every node is reachable from any other nodeEvery node is reachable from any other node
GG
JJ
FF
DD
AA
Connected graphConnected graph
GG
JJ
FF
DD
AA
EE
CC HH
75

76. Graphs and Their ApplicationsGraphs and Their Applications
 Graphs have many real-world applicationsGraphs have many real-world applications
Modeling a computer network like InternetModeling a computer network like Internet
 Routes are simple paths in the networkRoutes are simple paths in the network
Modeling a city mapModeling a city map
 Streets are edges, crossings are verticesStreets are edges, crossings are vertices
Social networksSocial networks
 People are nodes and their connections are edgesPeople are nodes and their connections are edges
State machinesState machines
 States are nodes, transitions are edgesStates are nodes, transitions are edges
76

77. Representing GraphsRepresenting Graphs
 Adjacency listAdjacency list
 Each node holds aEach node holds a
list of its neighborslist of its neighbors
 Adjacency matrixAdjacency matrix
 Each cell keepsEach cell keeps
whether and how twowhether and how two
nodes are connectednodes are connected
 Set of edgesSet of edges
00 11 00 11
00 00 11 00
11 00 00 00
00 11 00 00
1
2
3
4
1 2 3 4
{1,2} {1,4} {2,3} {3,1} {4,2}{1,2} {1,4} {2,3} {3,1} {4,2}
11  {2,{2,
4}4}
22  {3}{3}
33  {1}{1}
44  {2}{2}
22
4411
33
77

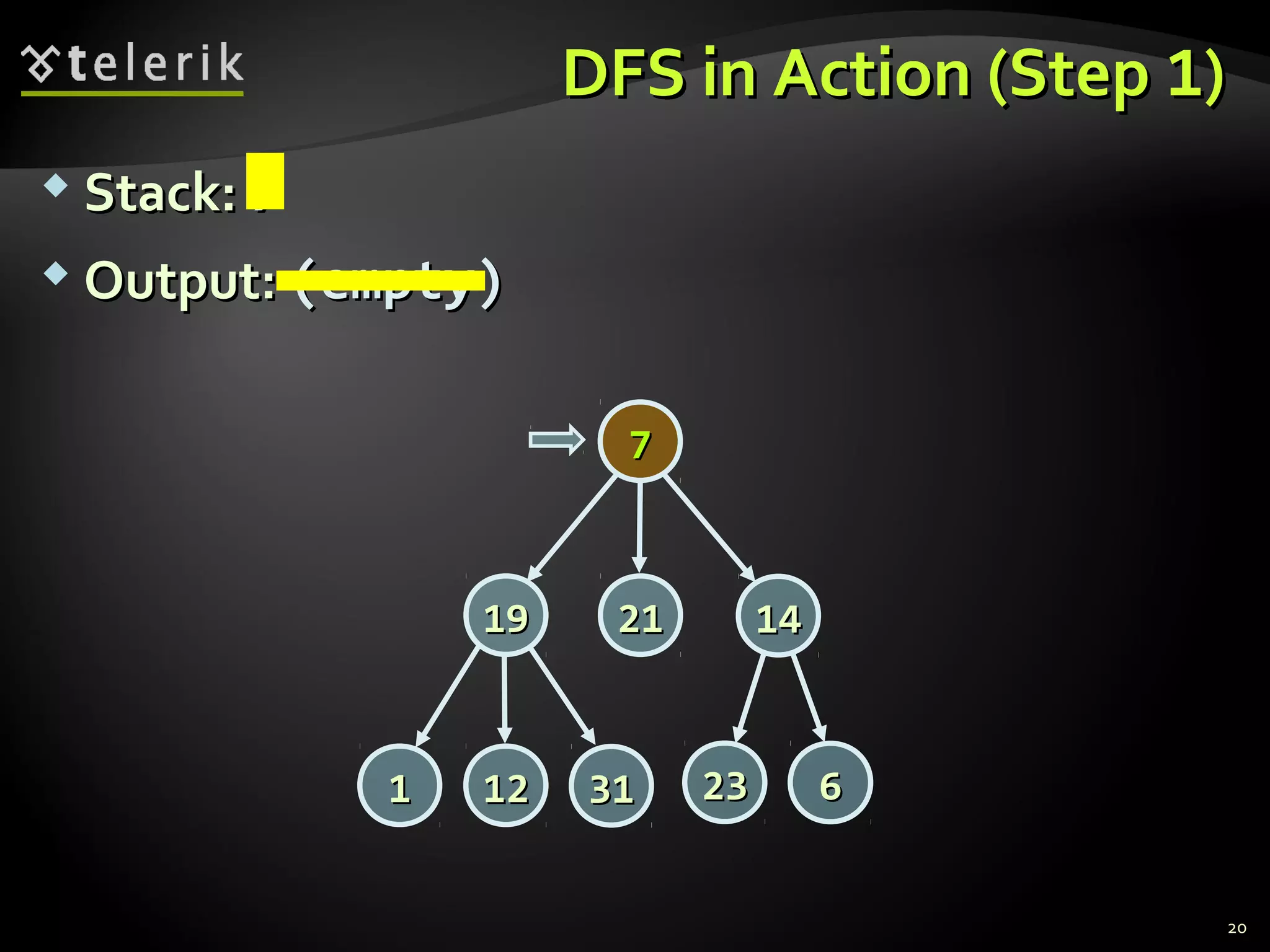
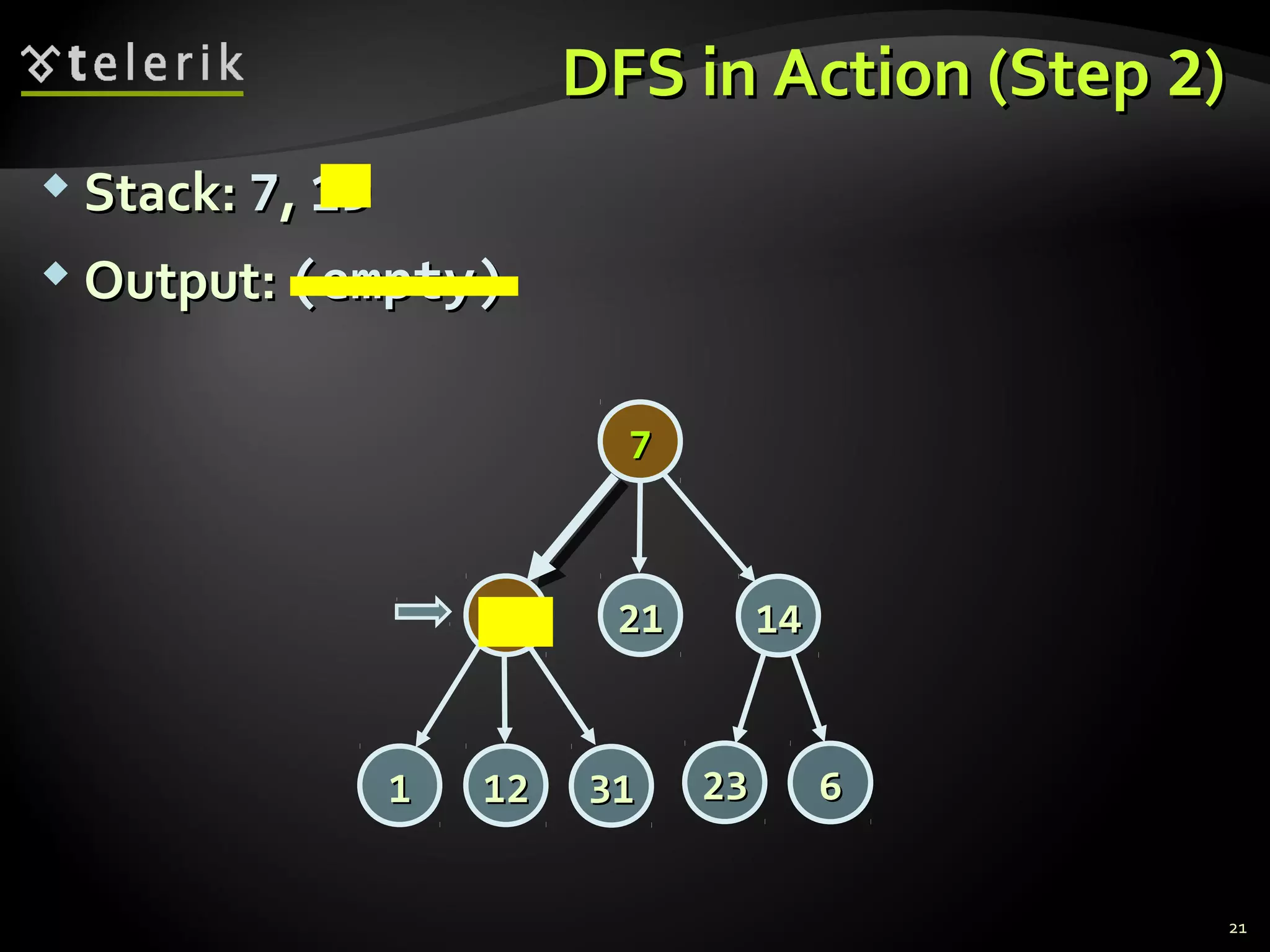
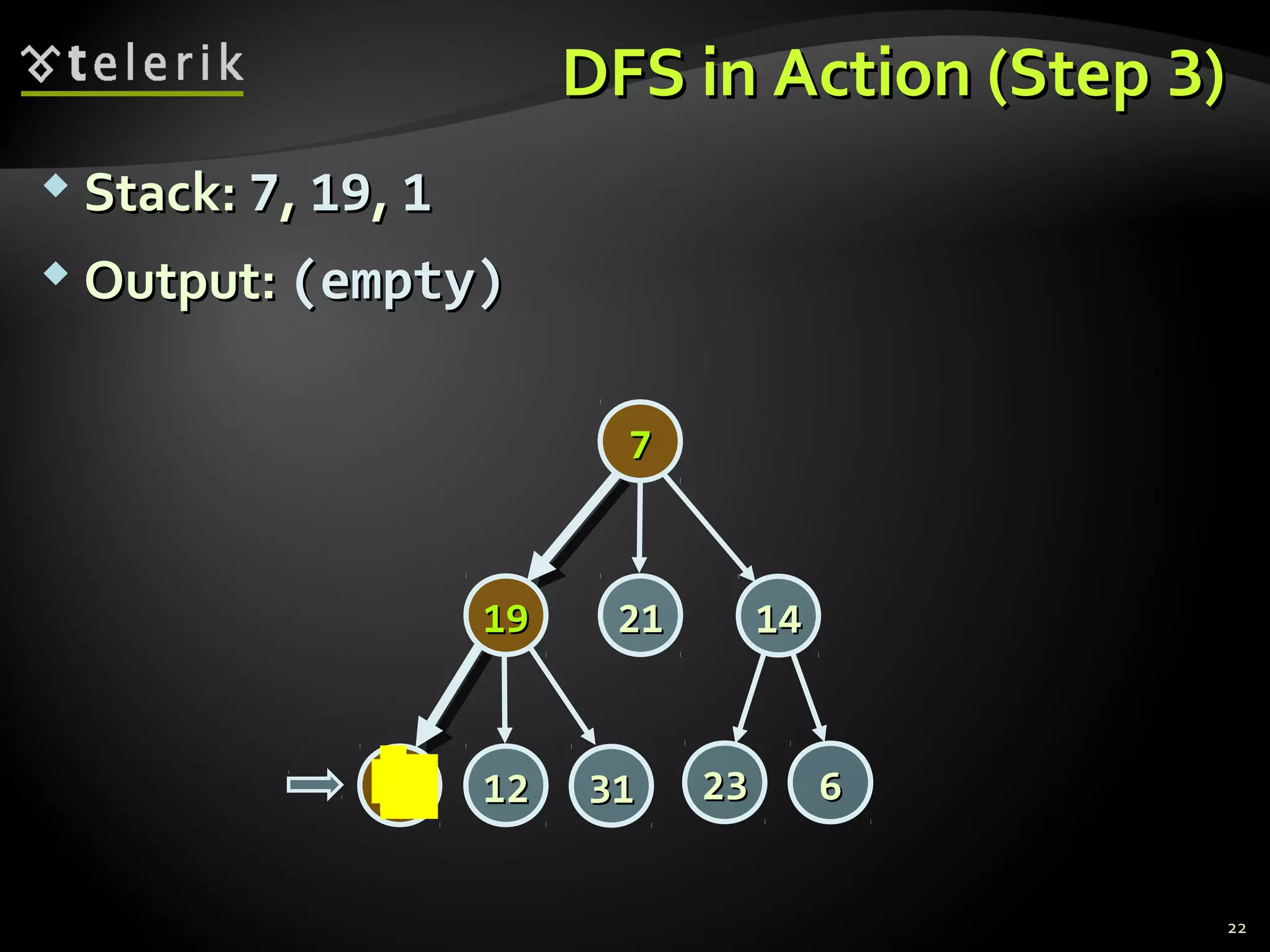
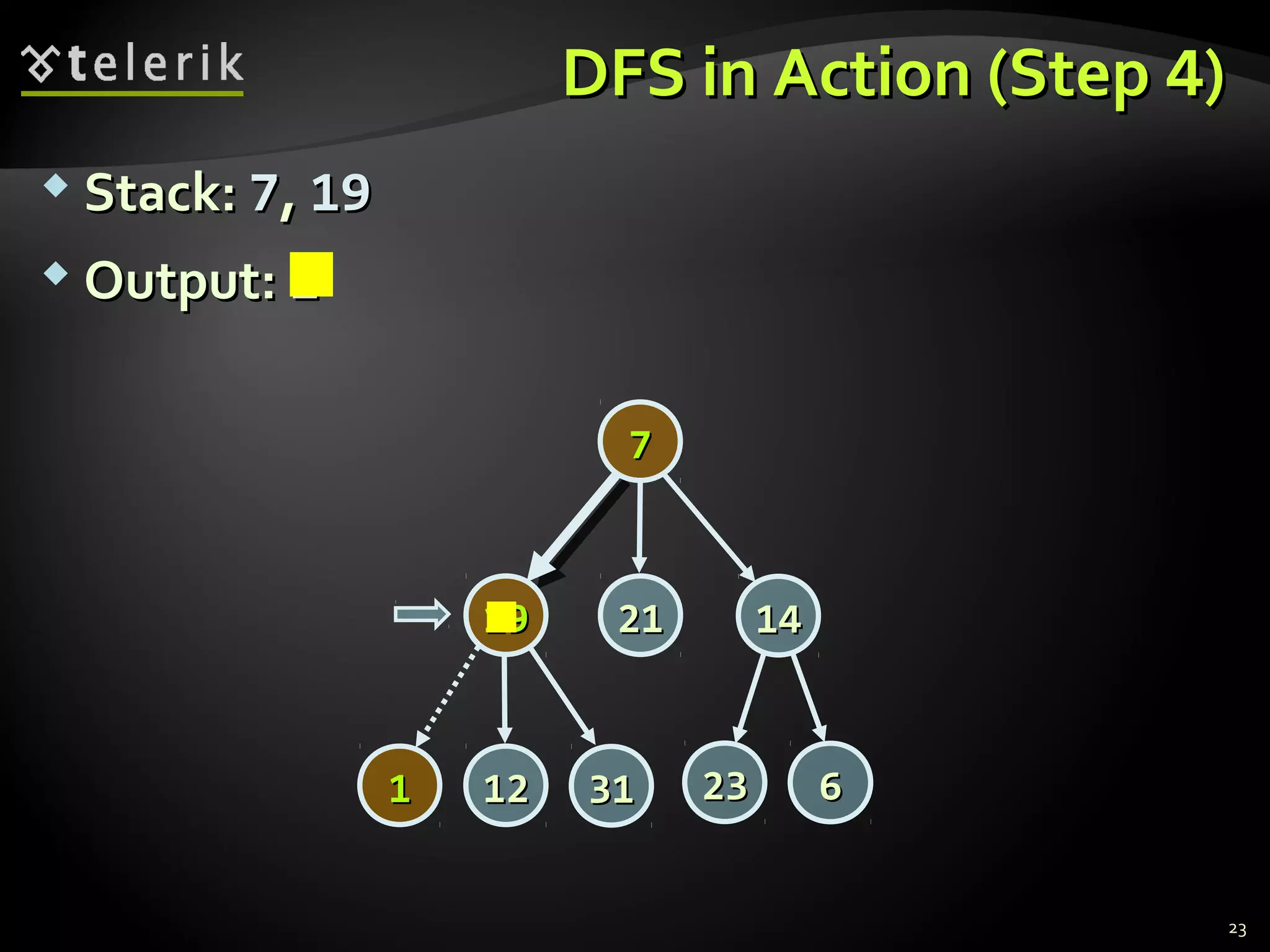
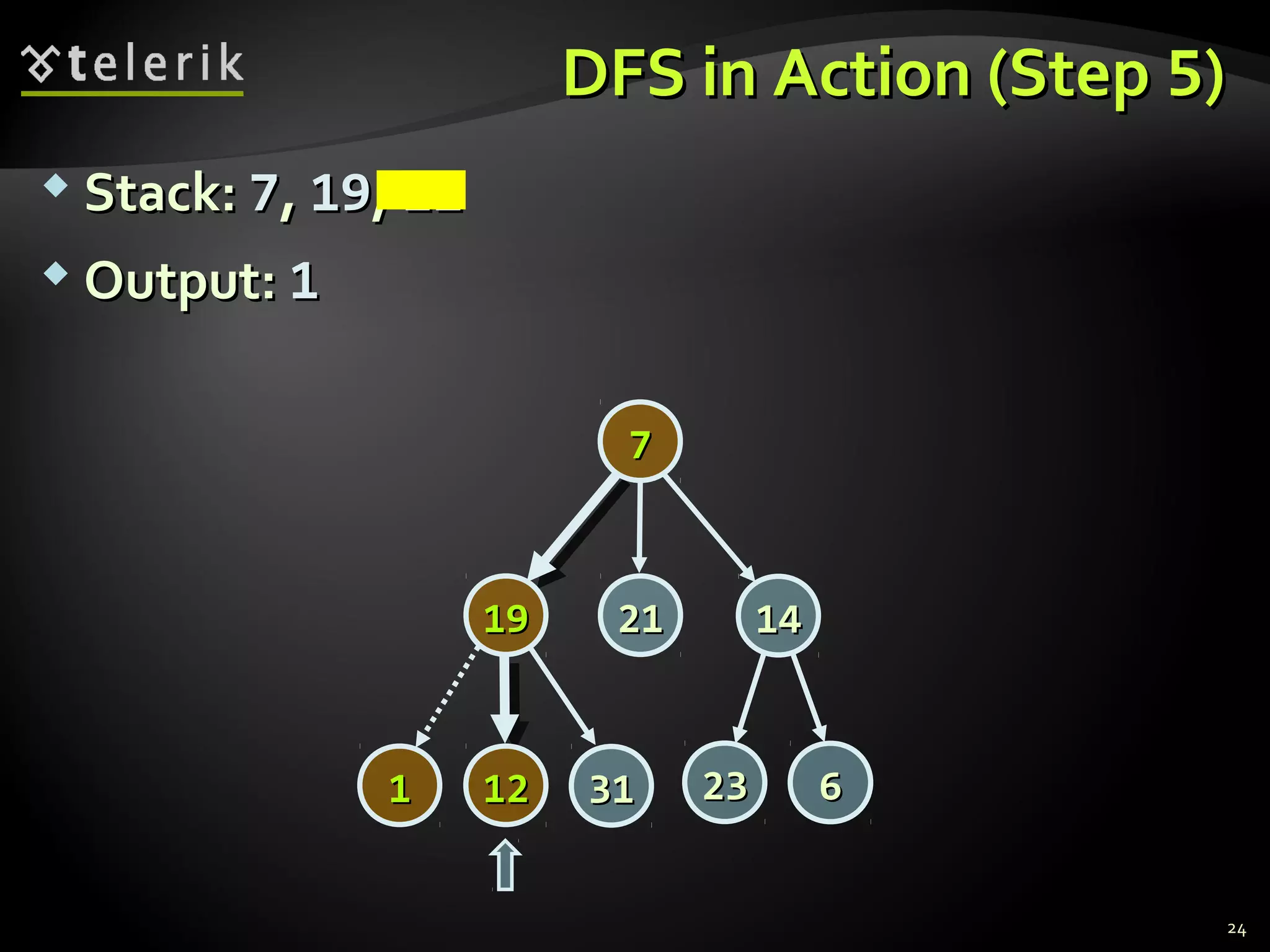
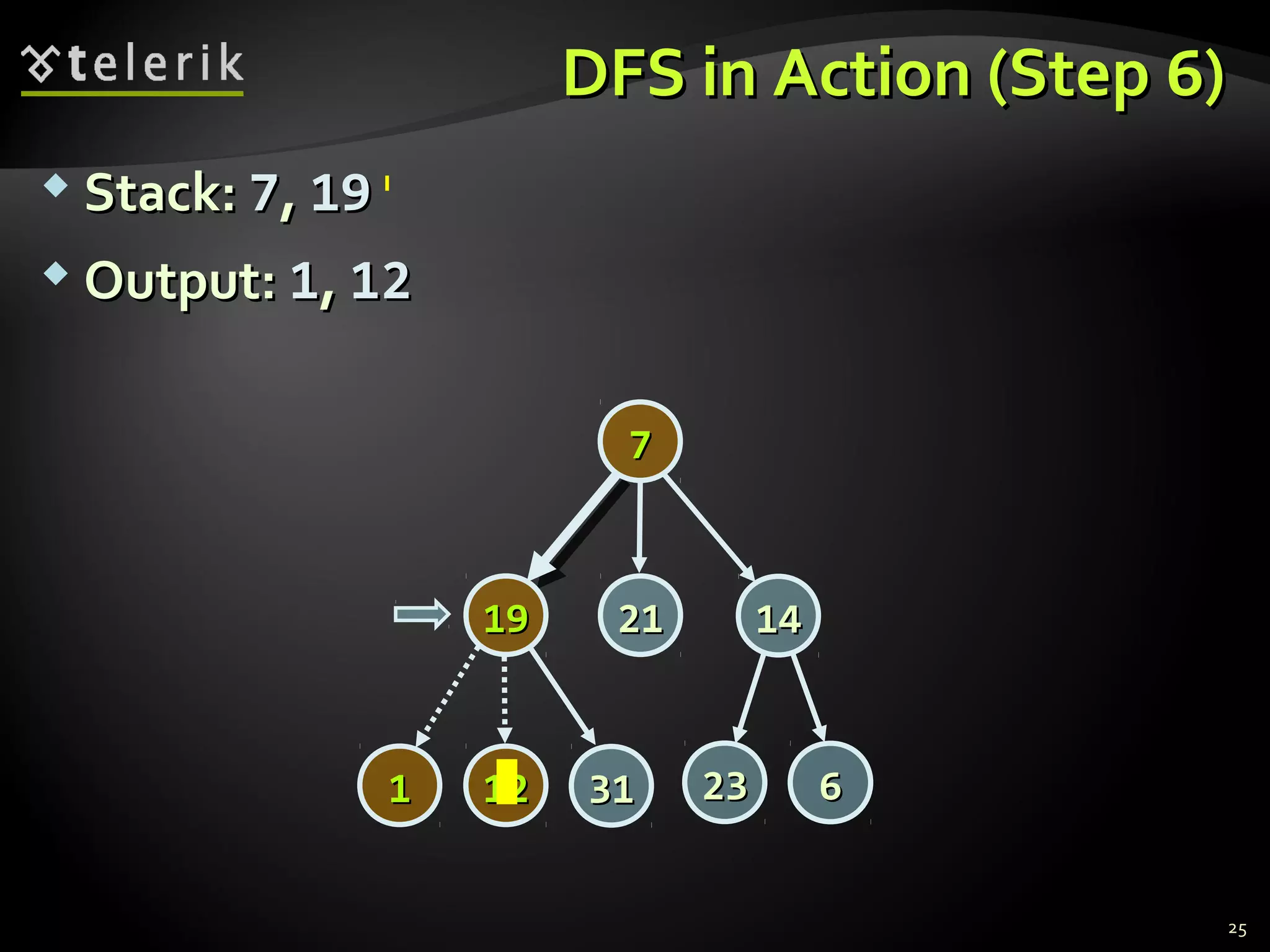
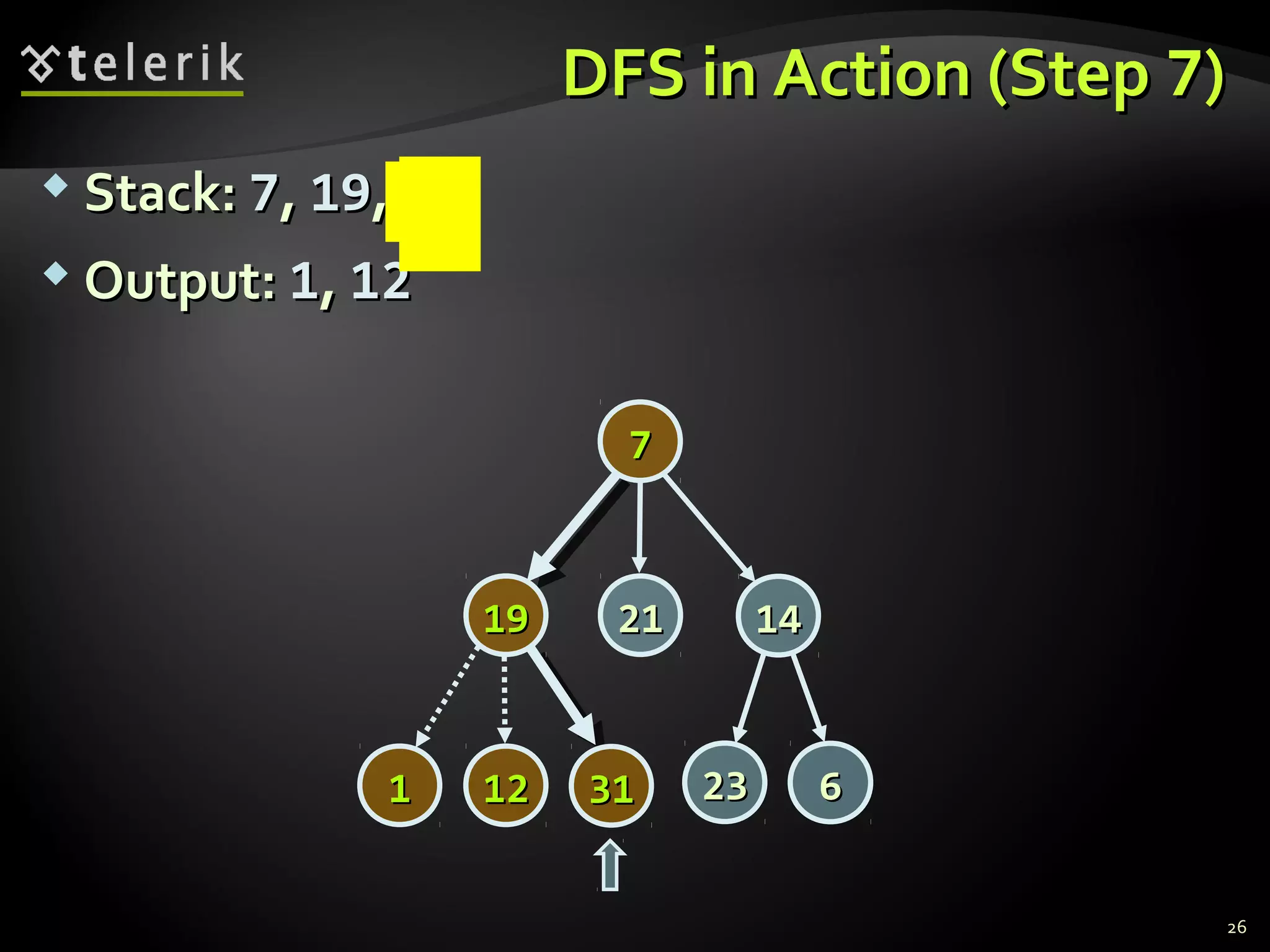
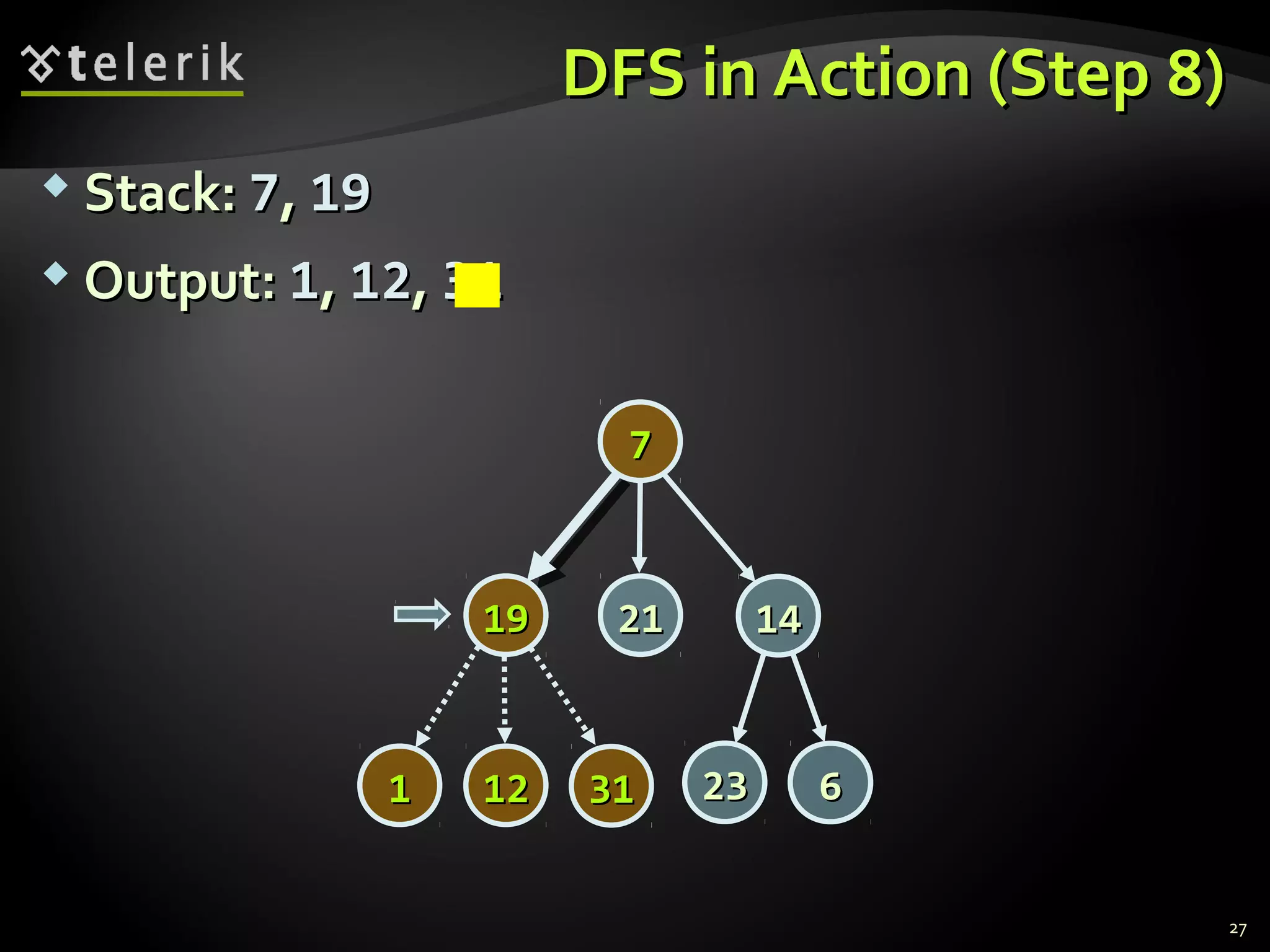
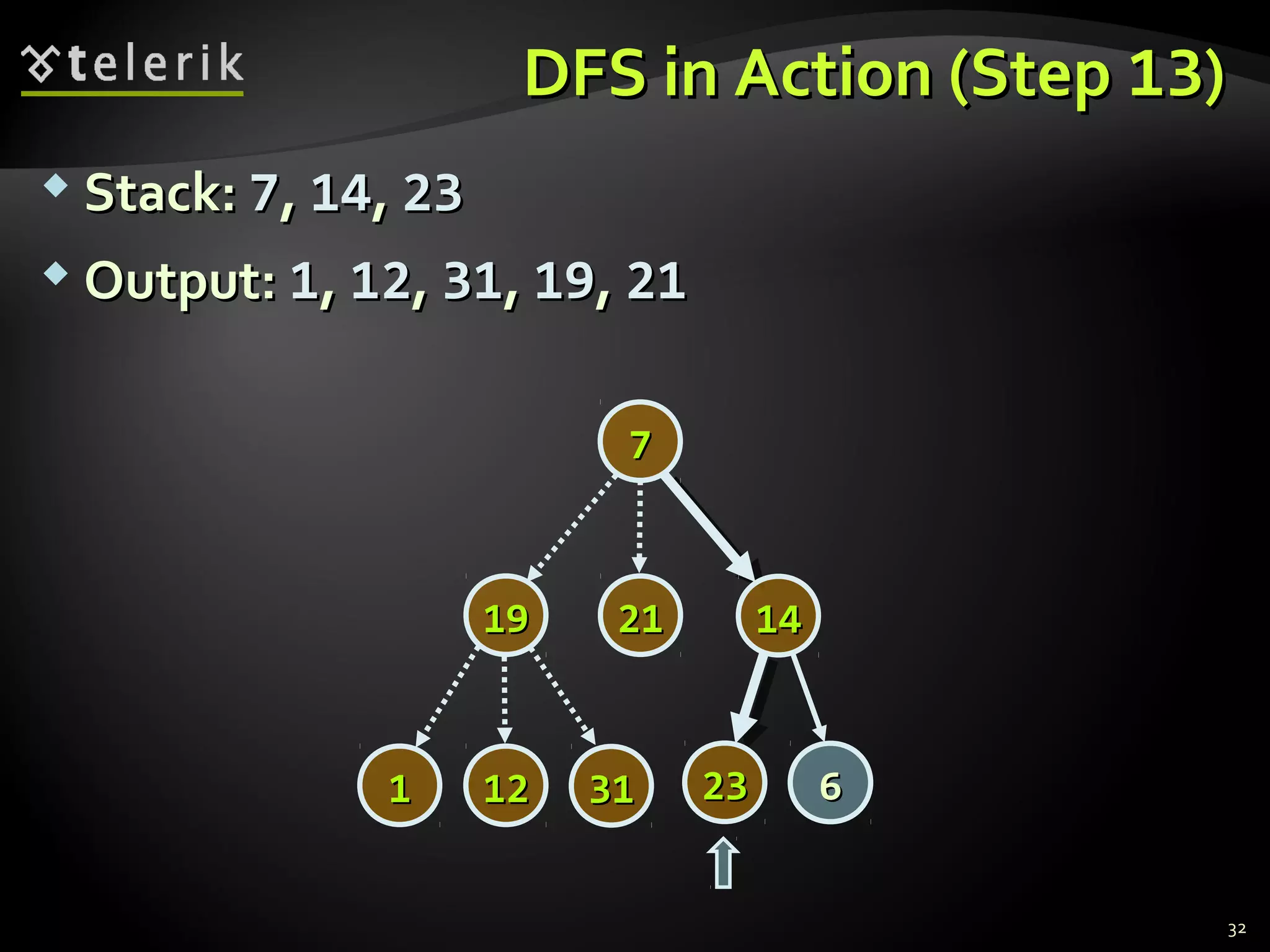
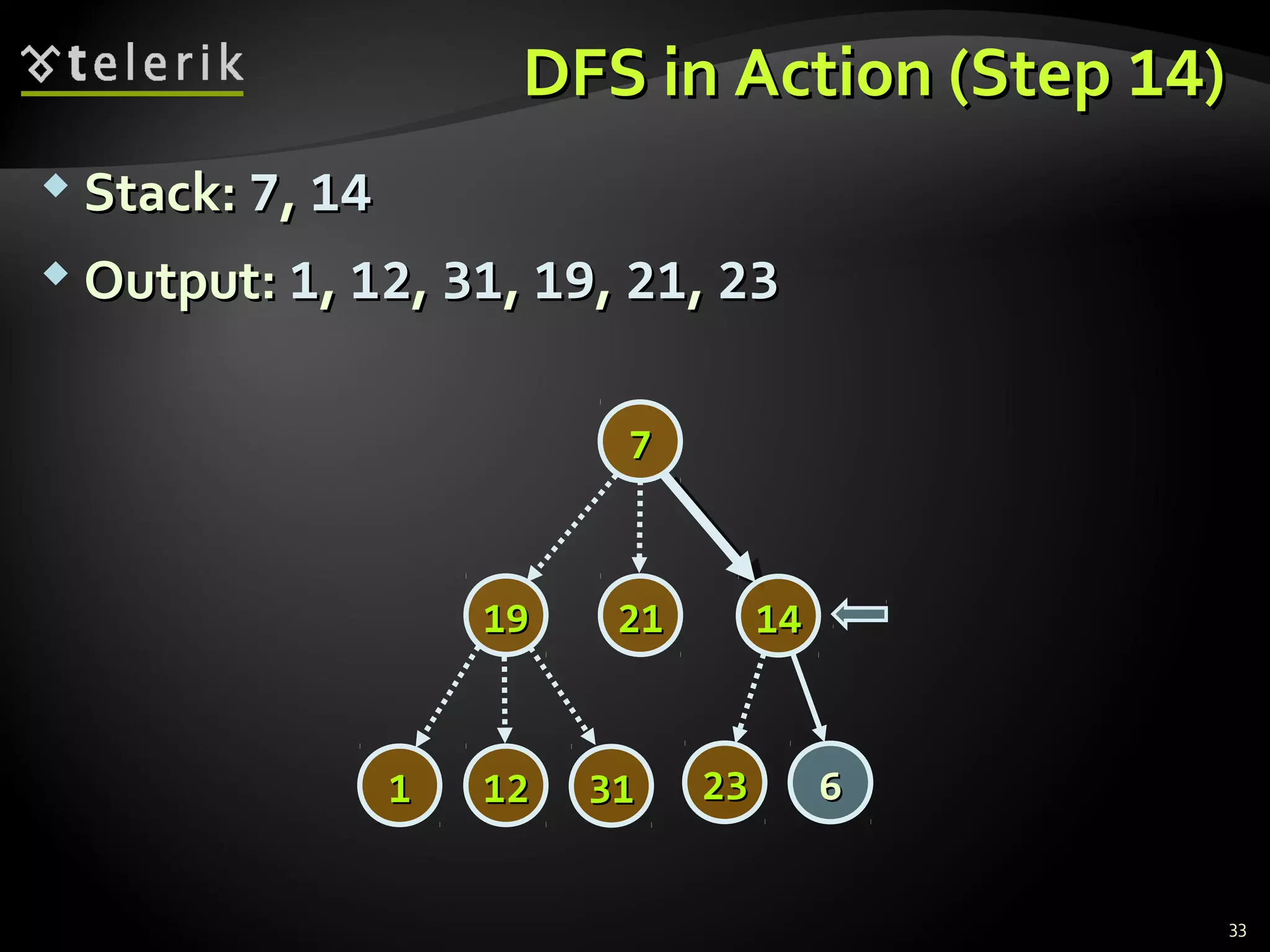
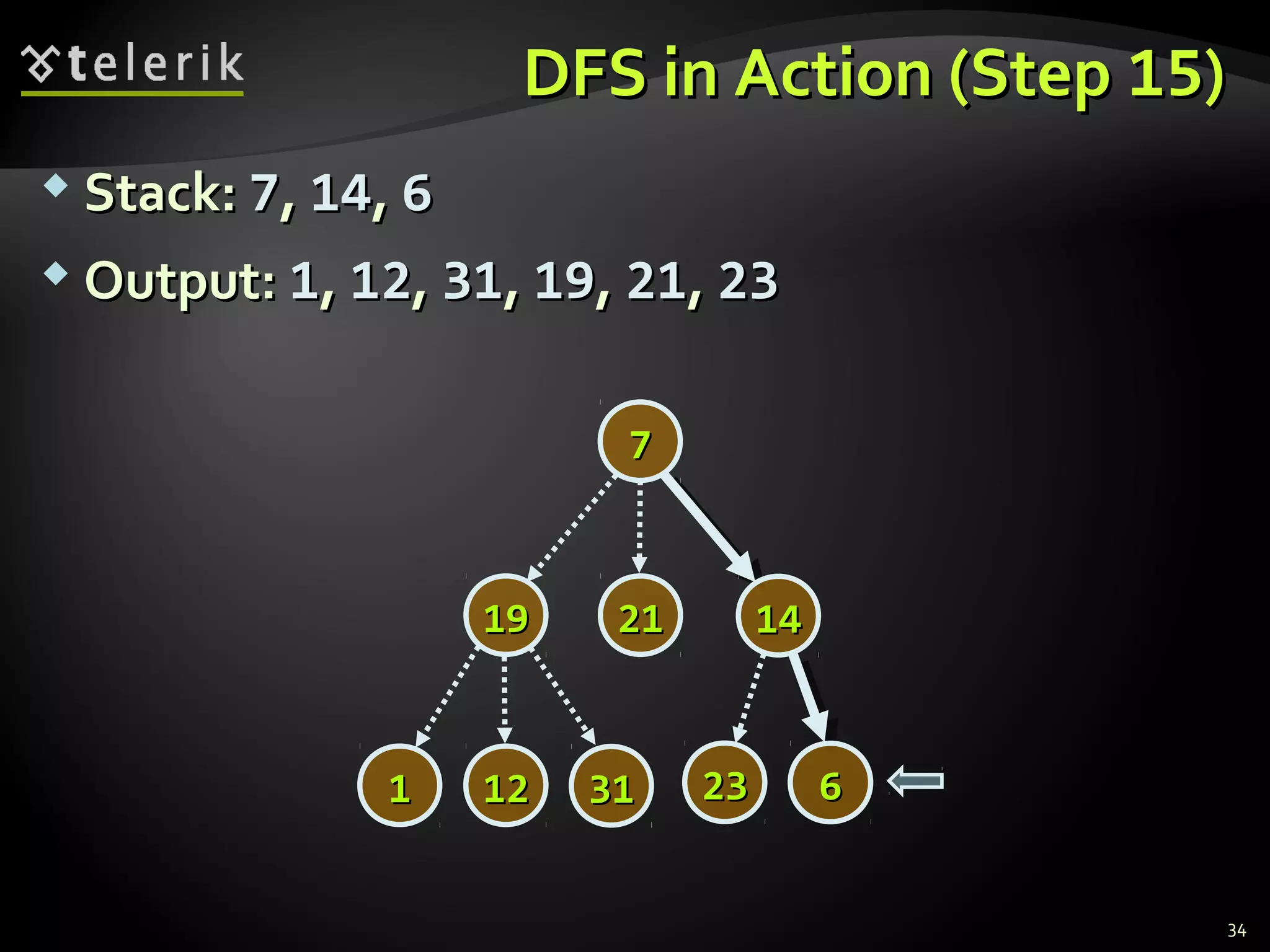
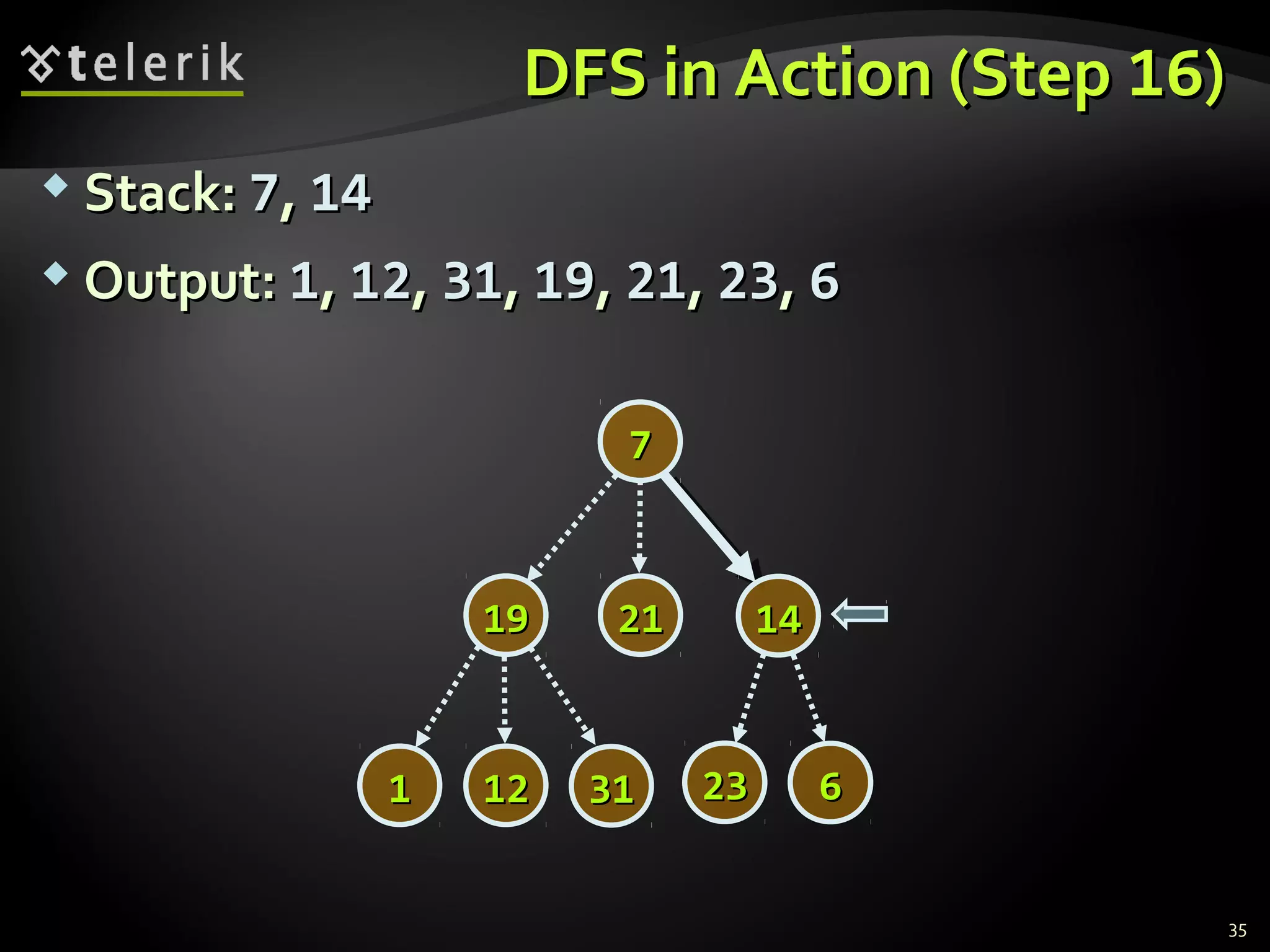
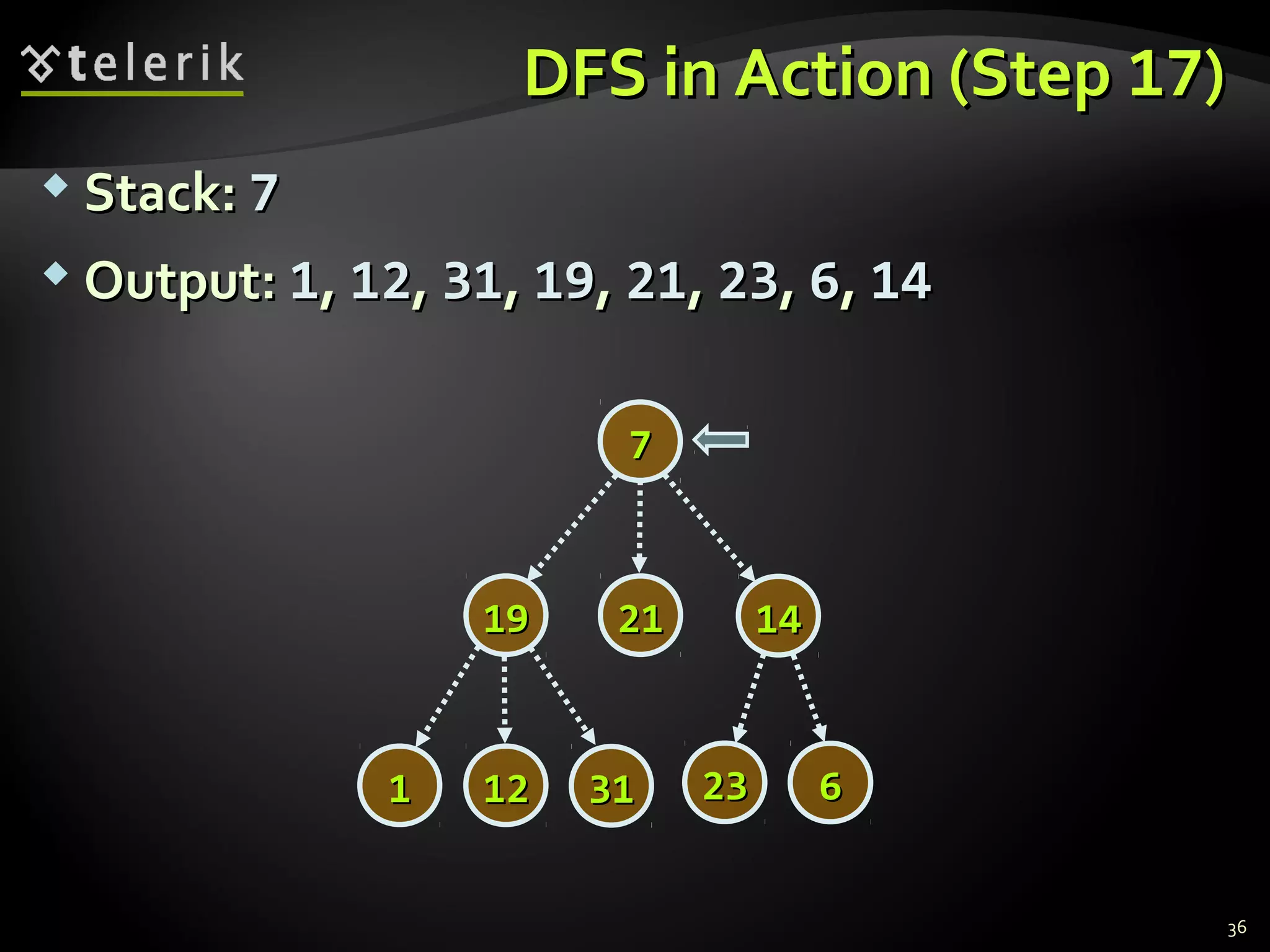
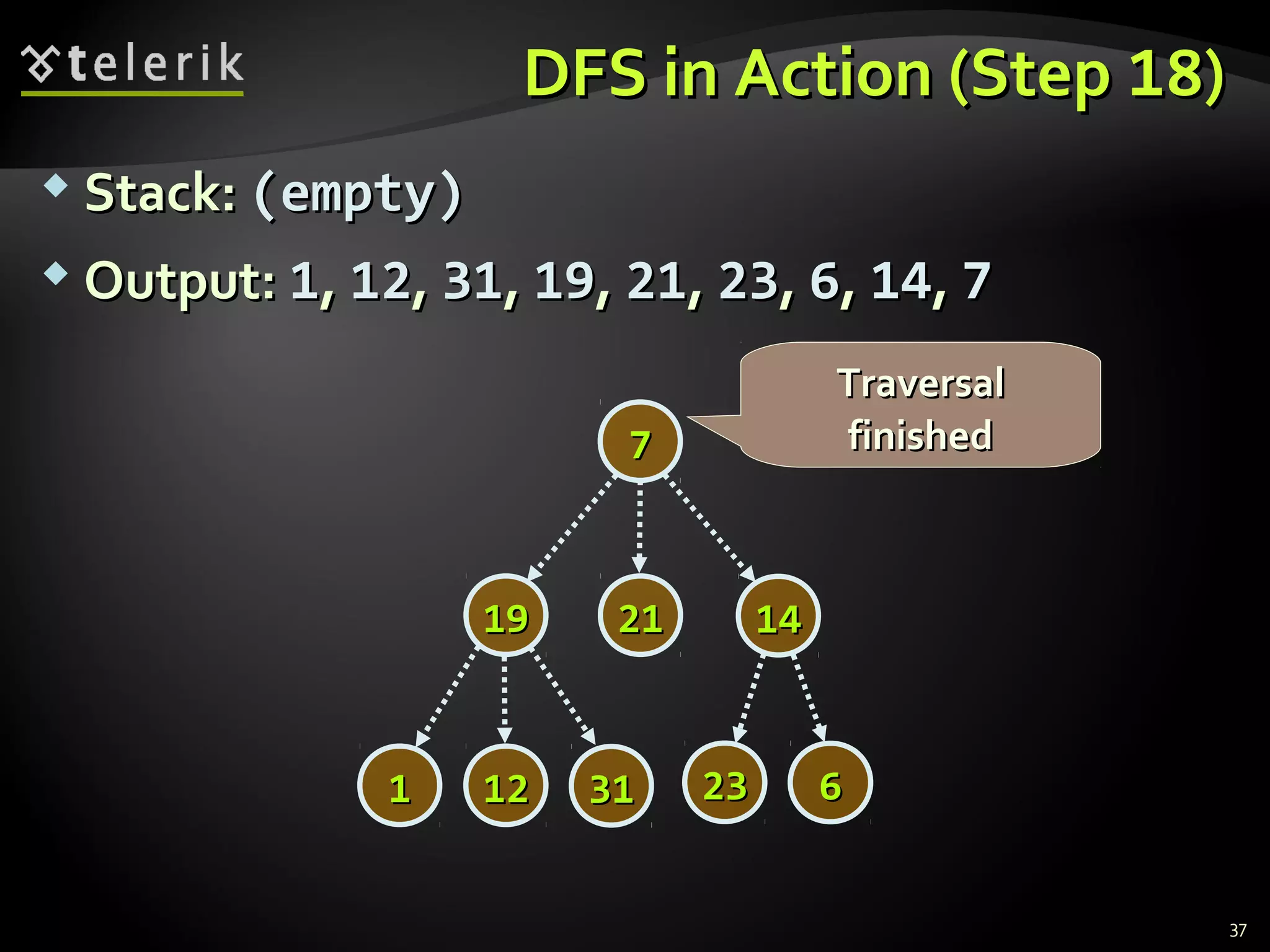
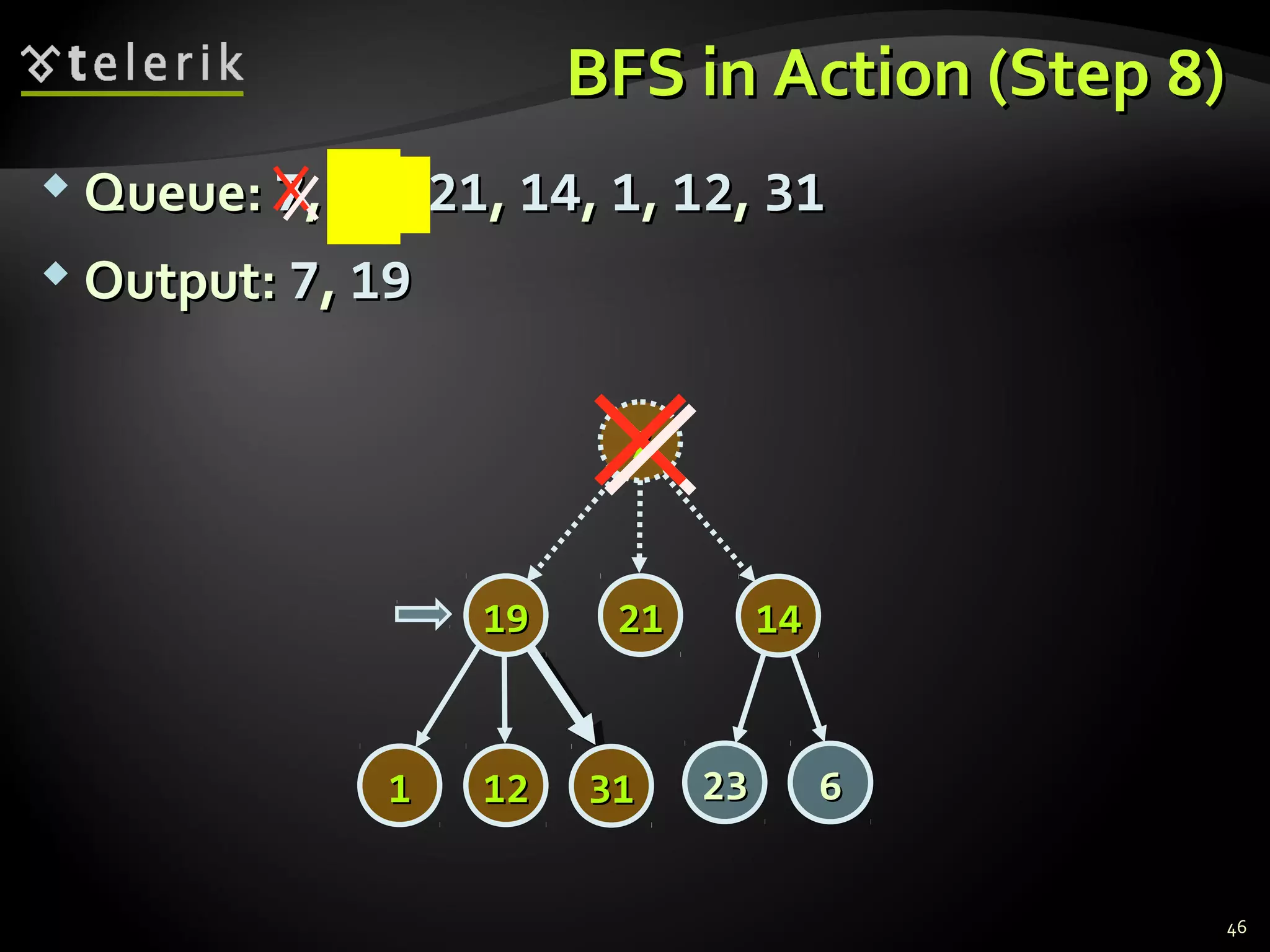
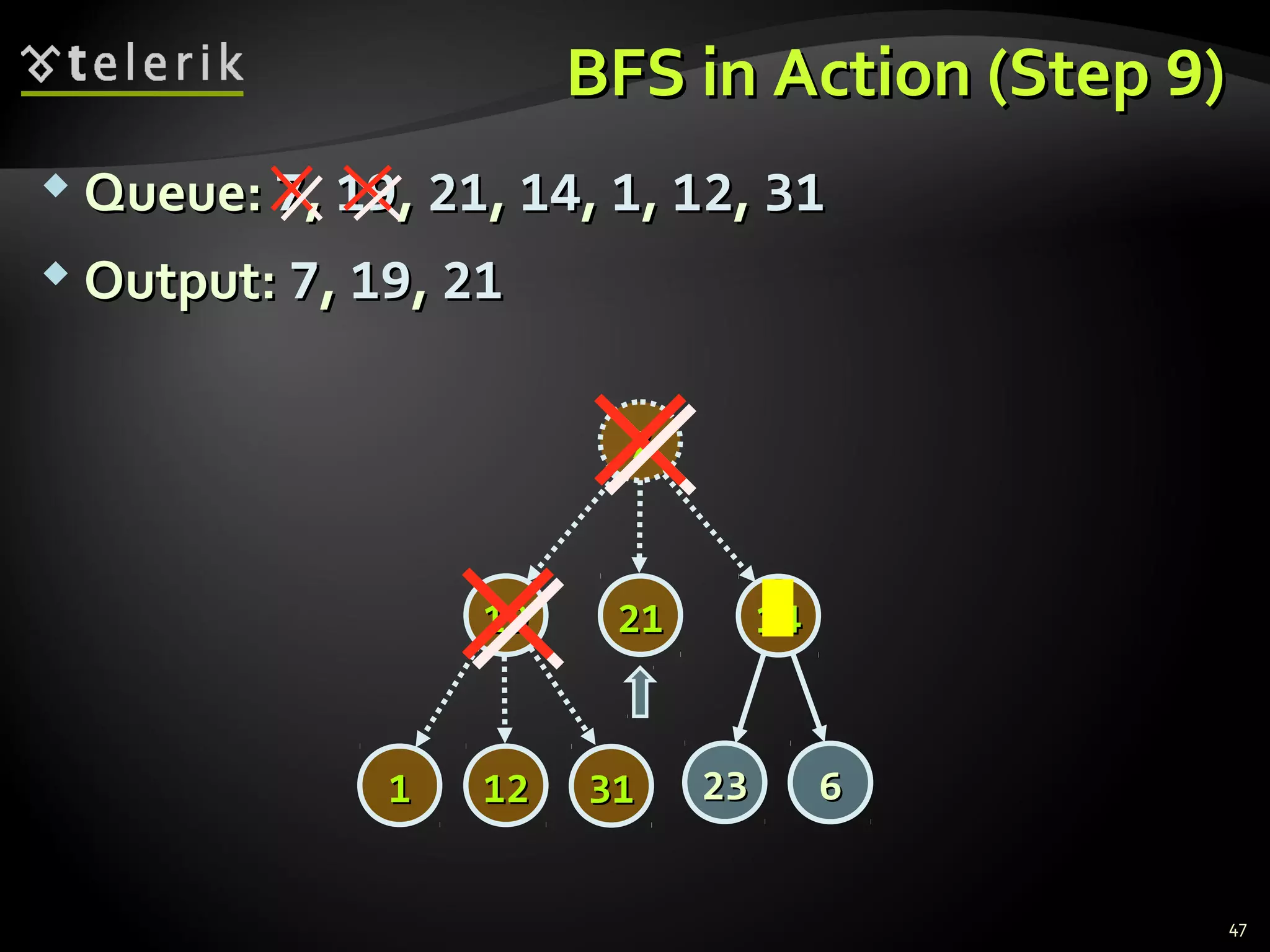
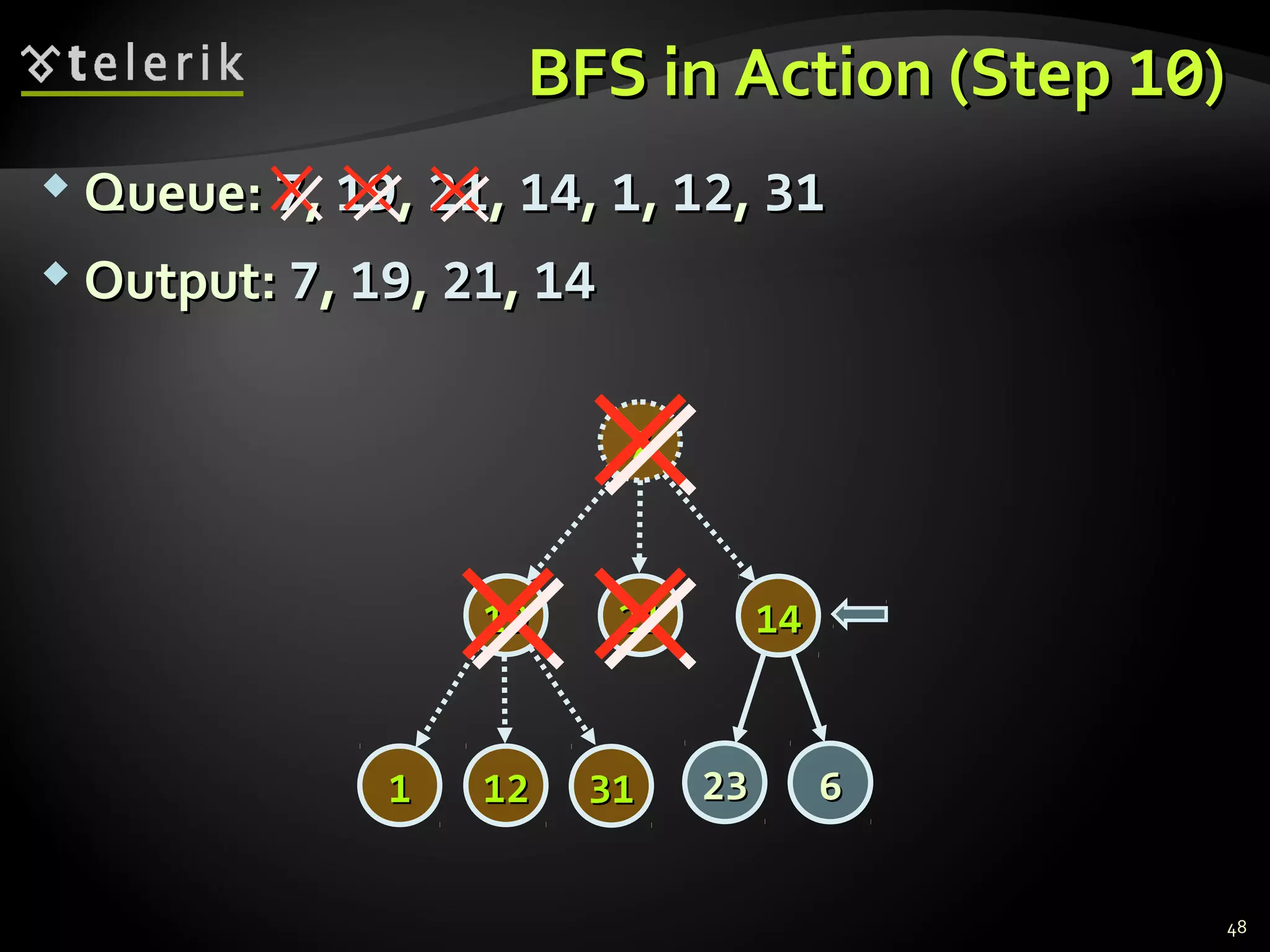
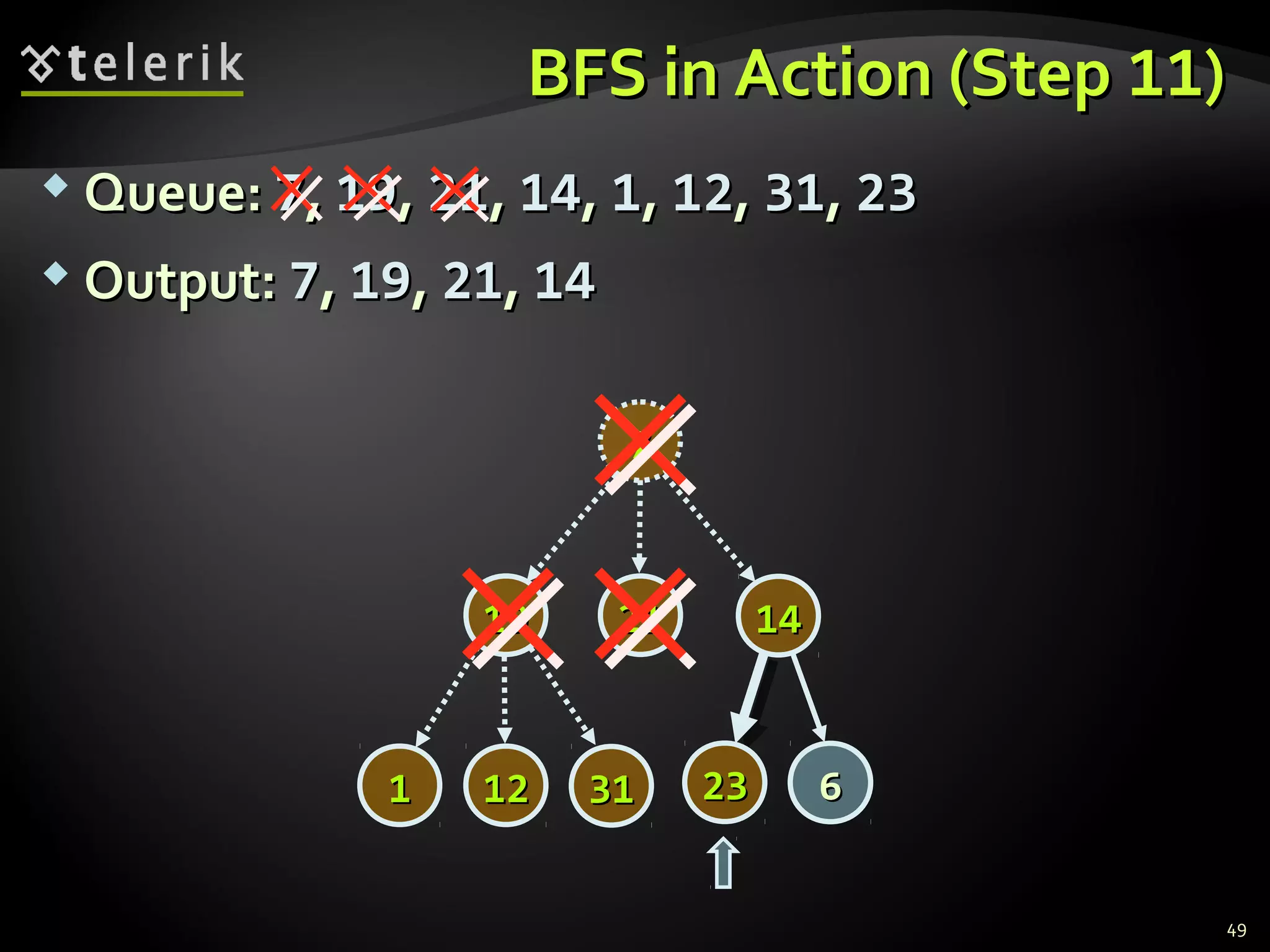
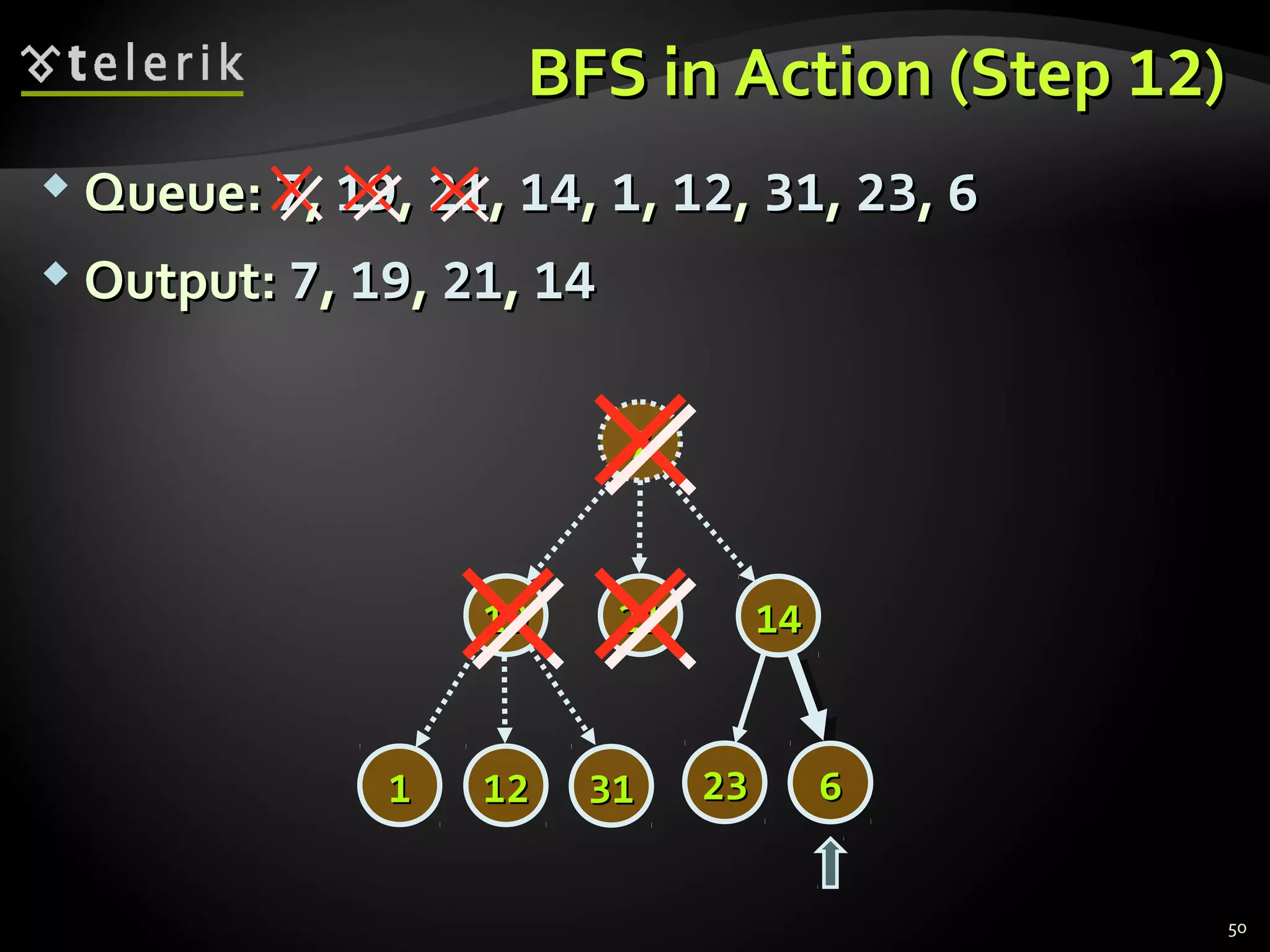
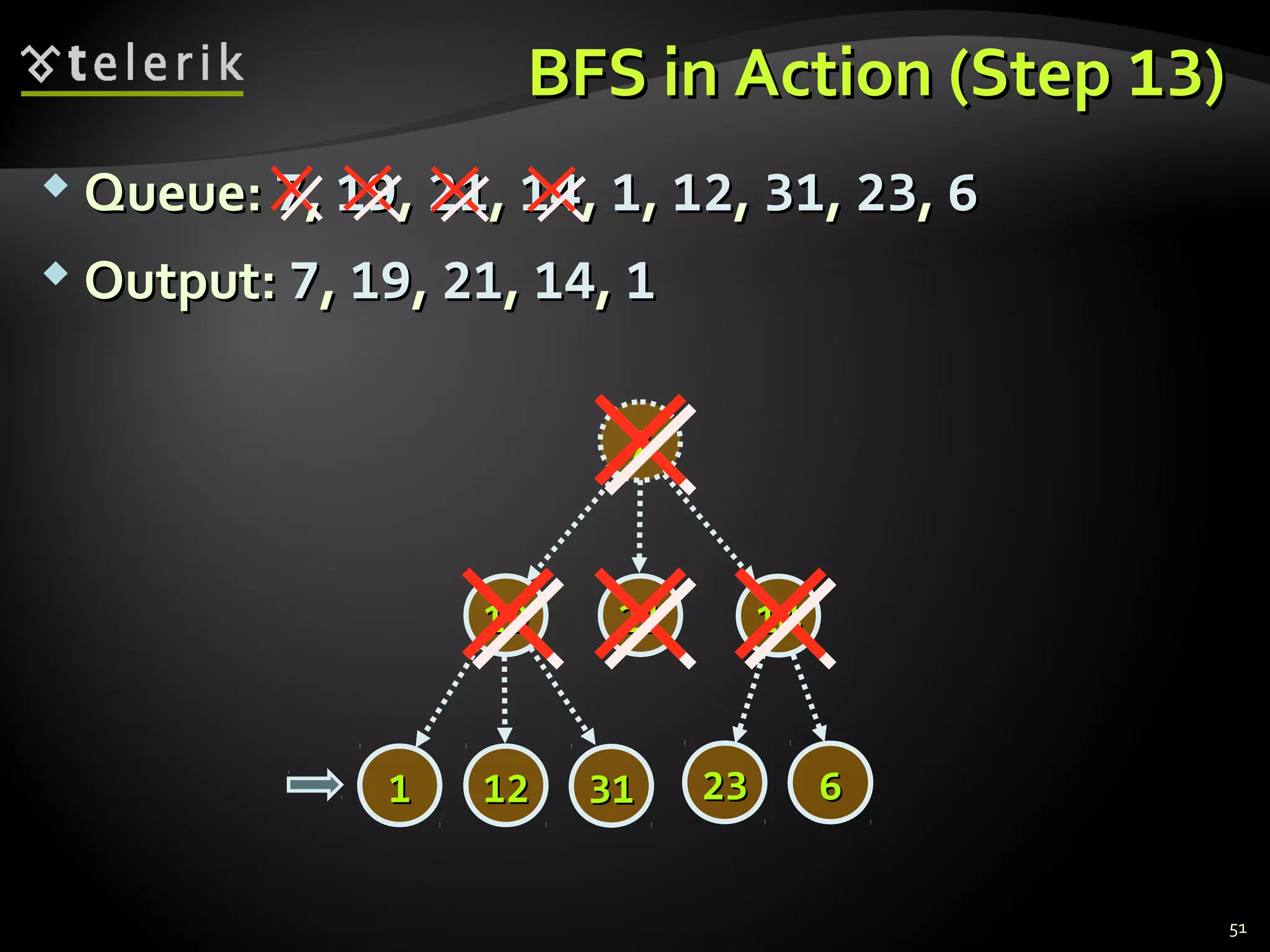
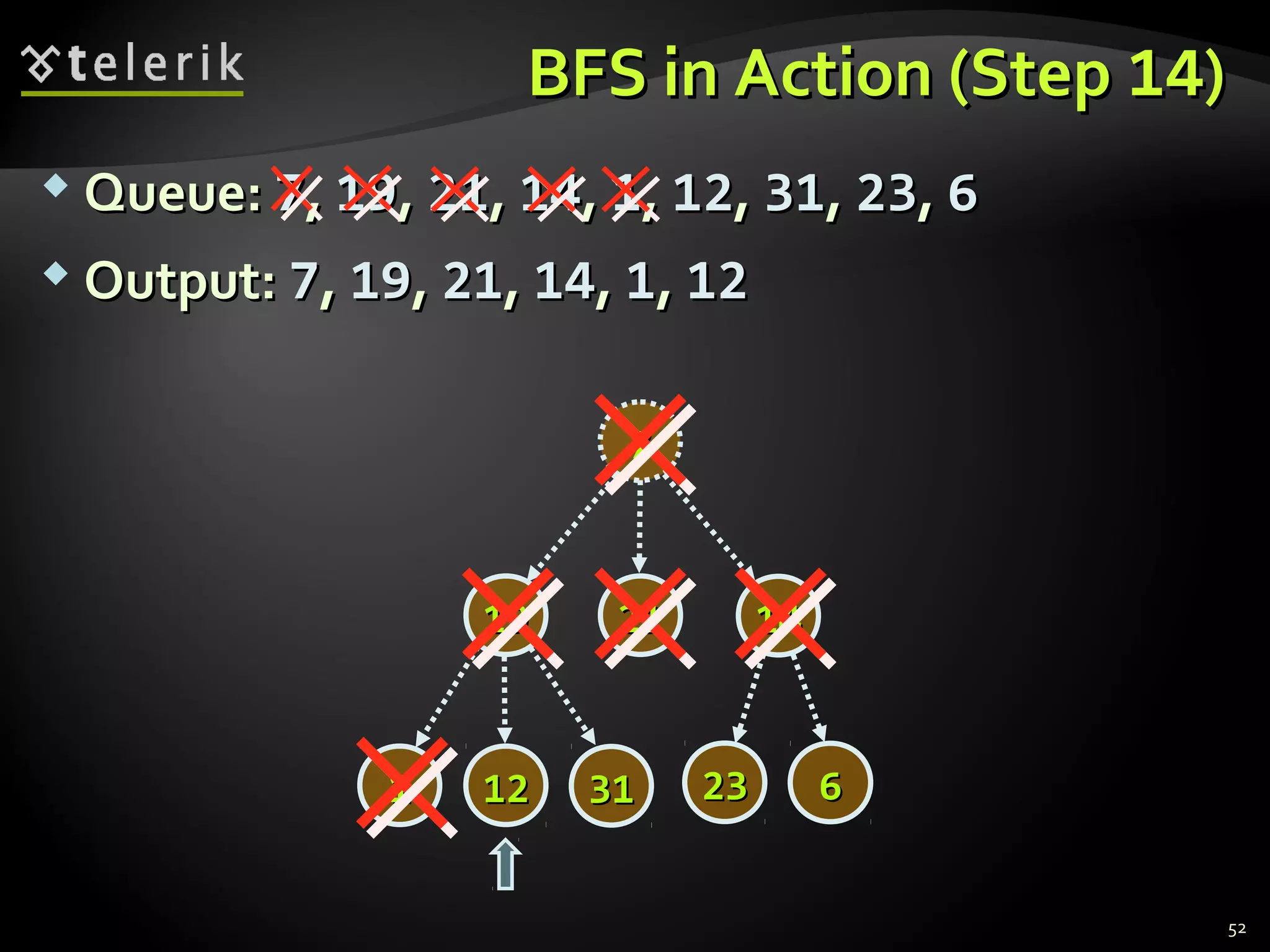
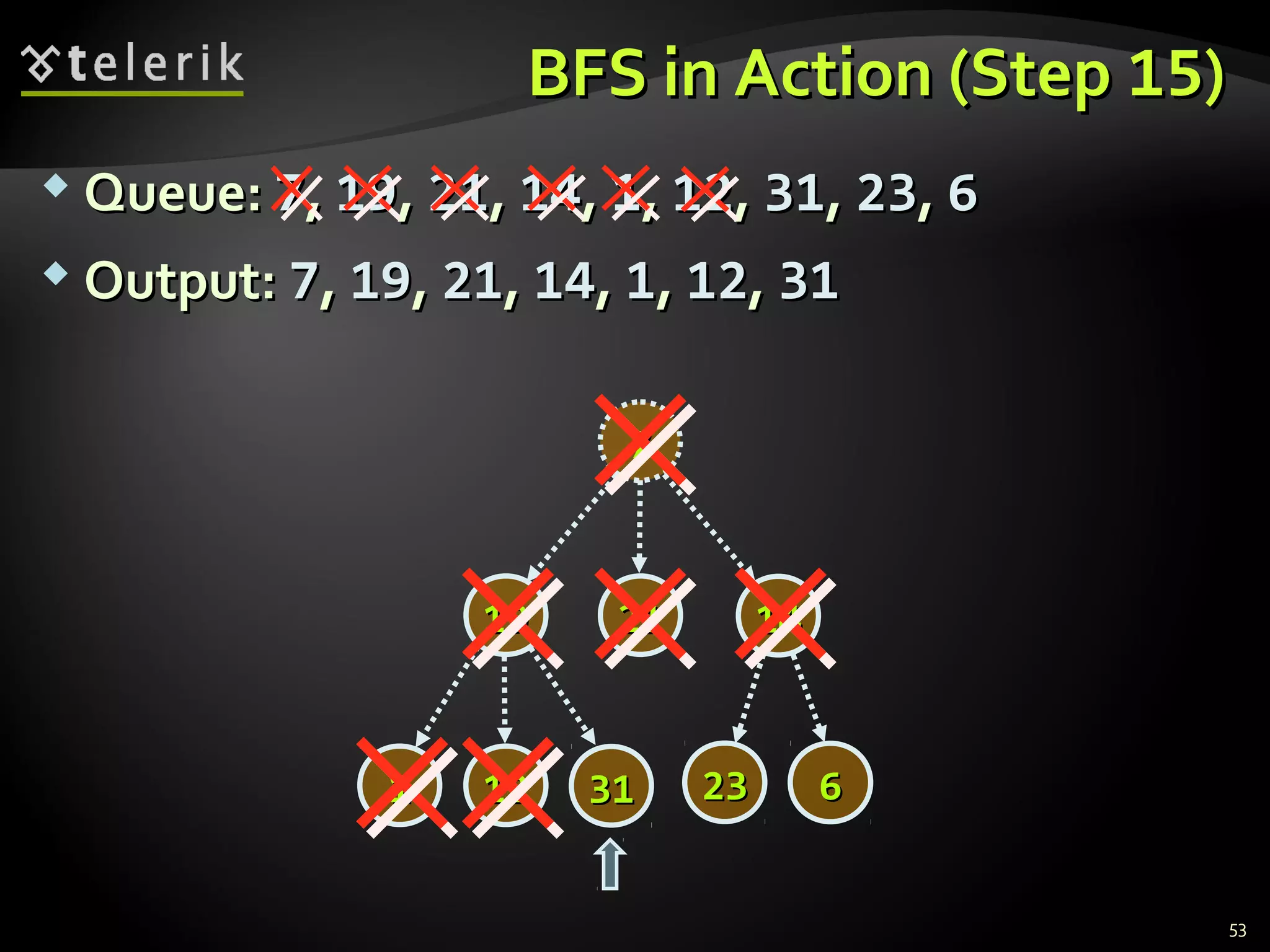
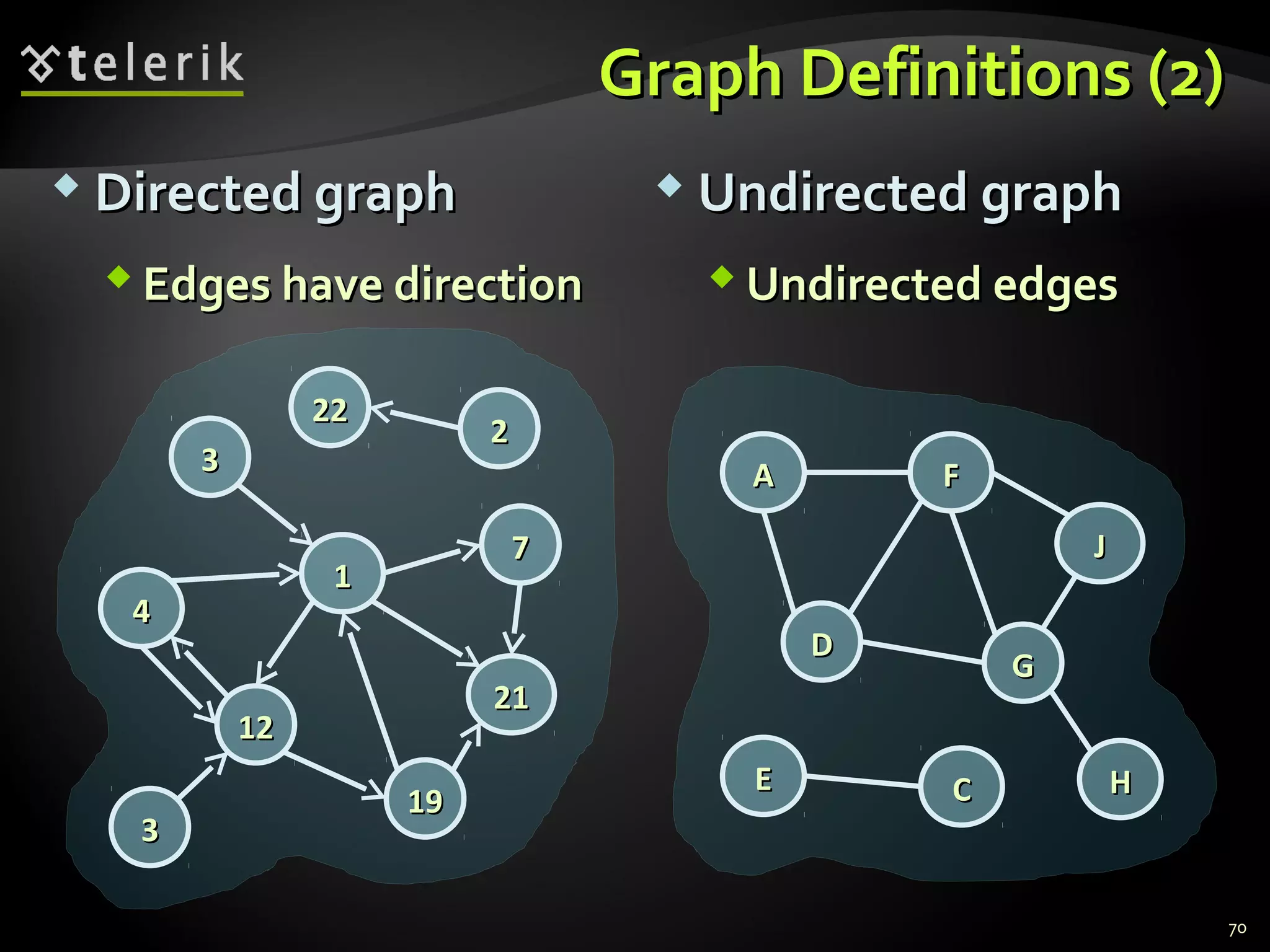
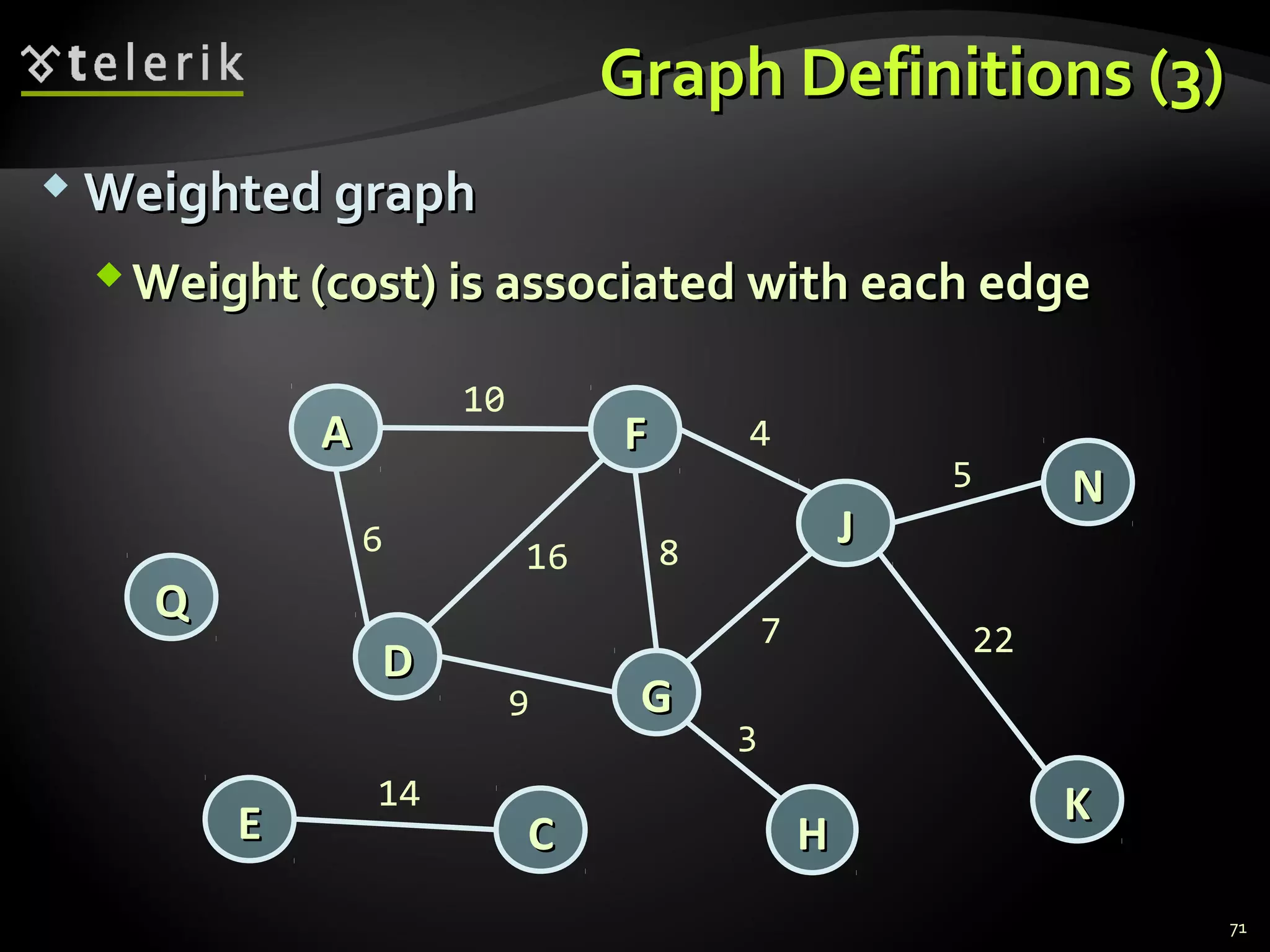
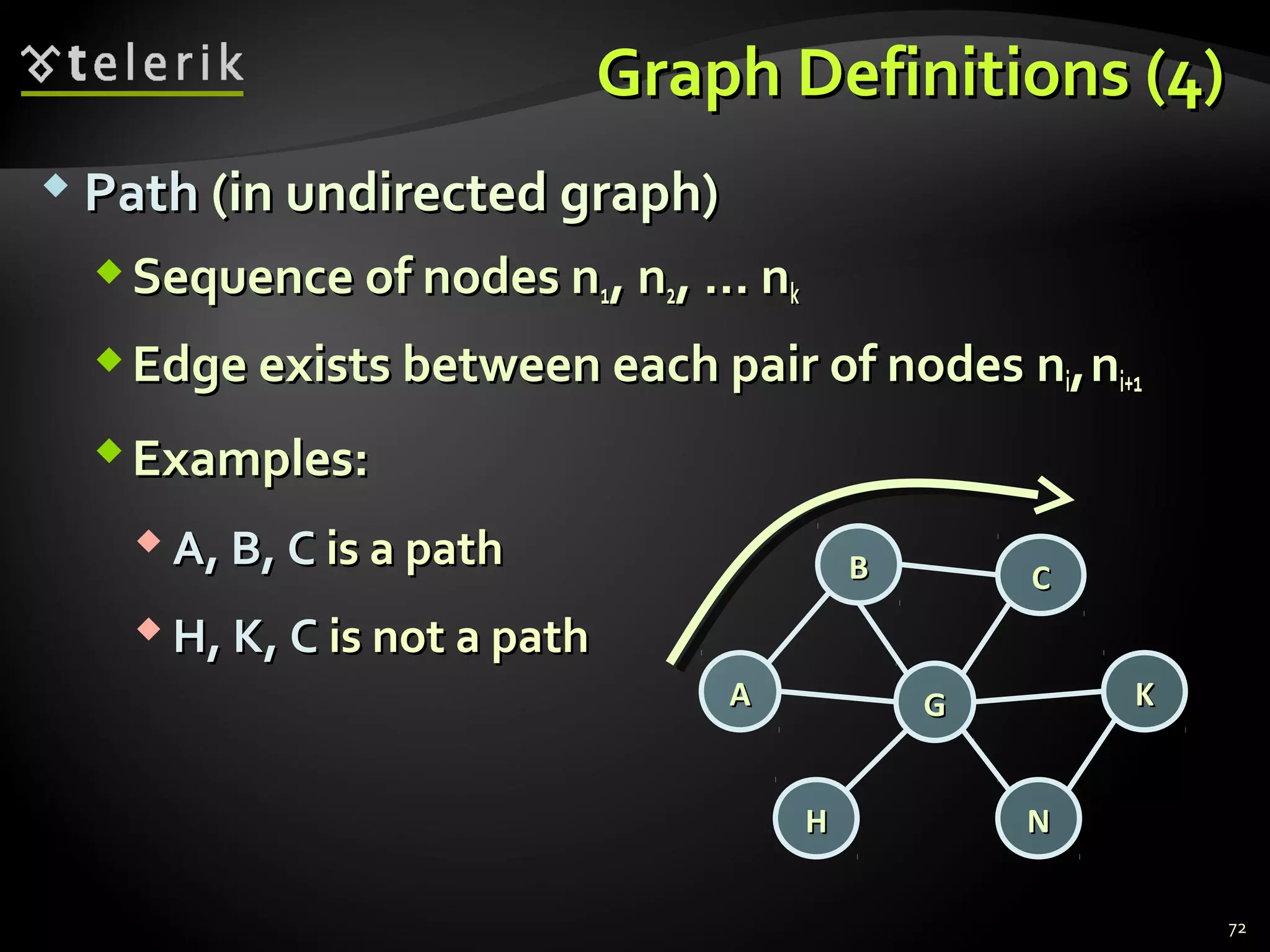
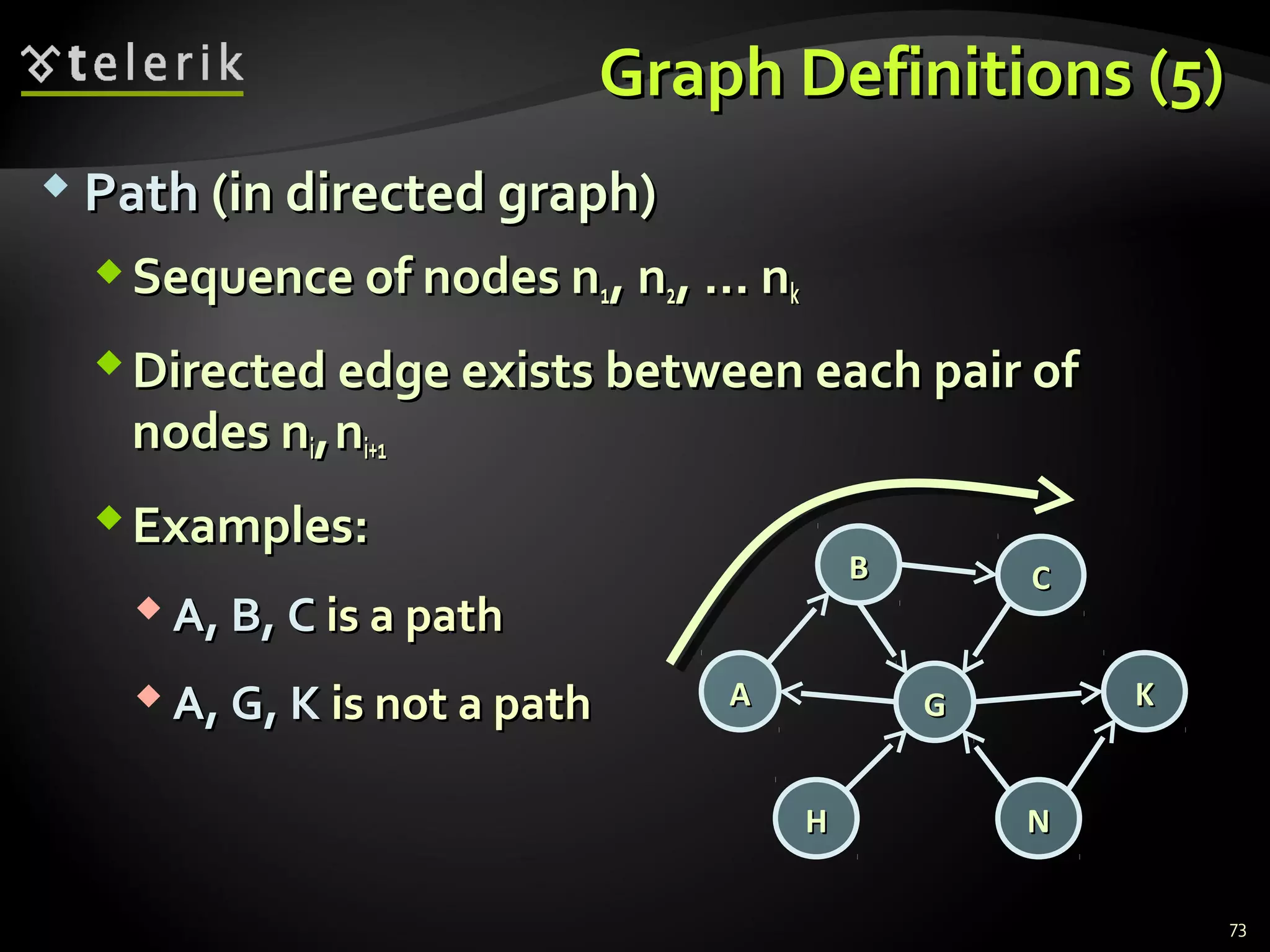
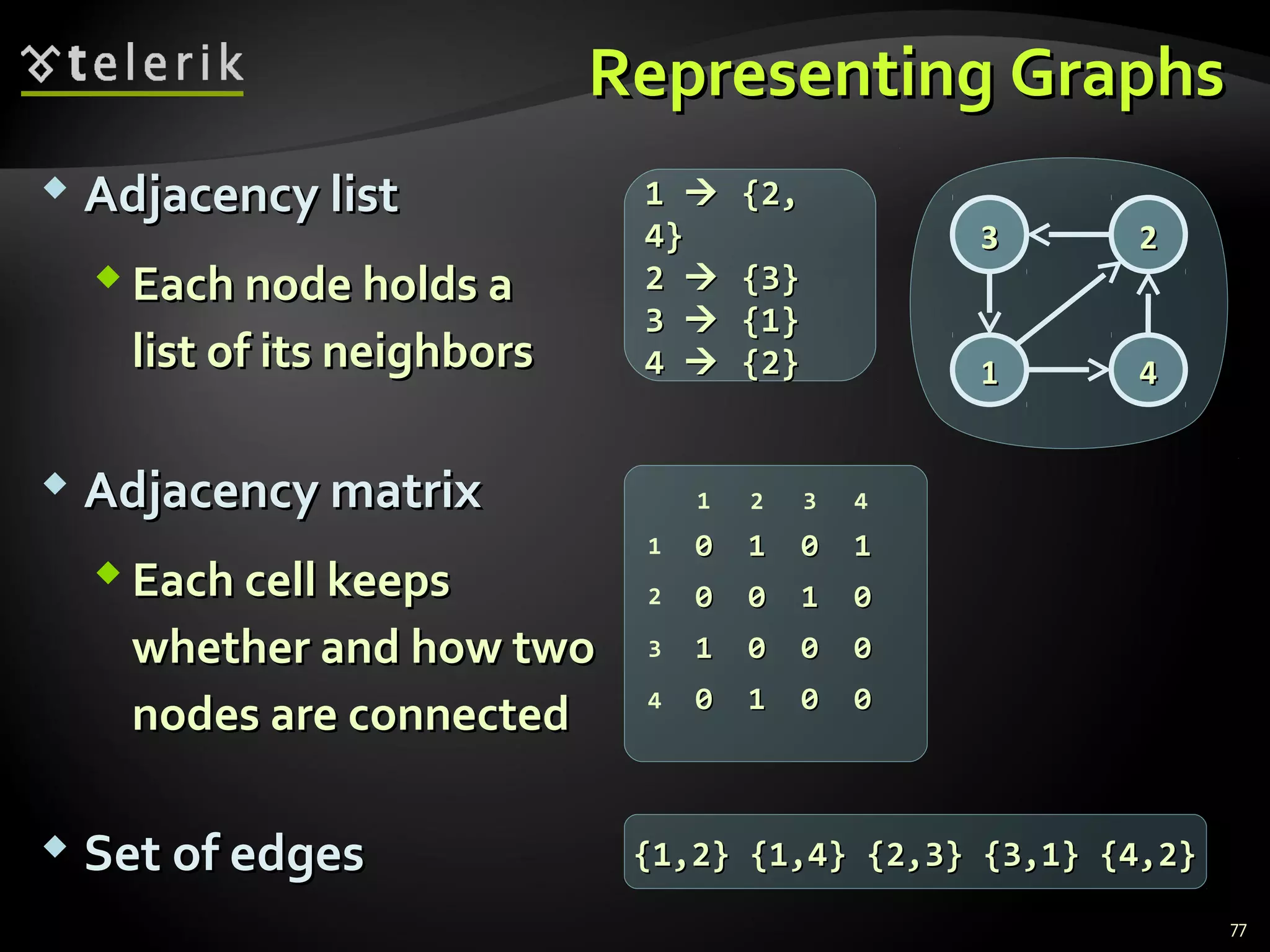
78. Representing Graphs in C#Representing Graphs in C#
public class Graphpublic class Graph
{{
int[][] childNodes;int[][] childNodes;
public Graph(int[][] nodes)public Graph(int[][] nodes)
{{
this.childNodes = nodes;this.childNodes = nodes;
}}
}}
Graph g = new Graph(new int[][] {Graph g = new Graph(new int[][] {
new int[] {3, 6}, // successors of vertice 0new int[] {3, 6}, // successors of vertice 0
new int[] {2, 3, 4, 5, 6}, // successors of vertice 1new int[] {2, 3, 4, 5, 6}, // successors of vertice 1
new int[] {1, 4, 5}, // successors of vertice 2new int[] {1, 4, 5}, // successors of vertice 2
new int[] {0, 1, 5}, // successors of vertice 3new int[] {0, 1, 5}, // successors of vertice 3
new int[] {1, 2, 6}, // successors of vertice 4new int[] {1, 2, 6}, // successors of vertice 4
new int[] {1, 2, 3}, // successors of vertice 5new int[] {1, 2, 3}, // successors of vertice 5
new int[] {0, 1, 4} // successors of vertice 6new int[] {0, 1, 4} // successors of vertice 6
});});
00
66
44
11
55
22
33
78

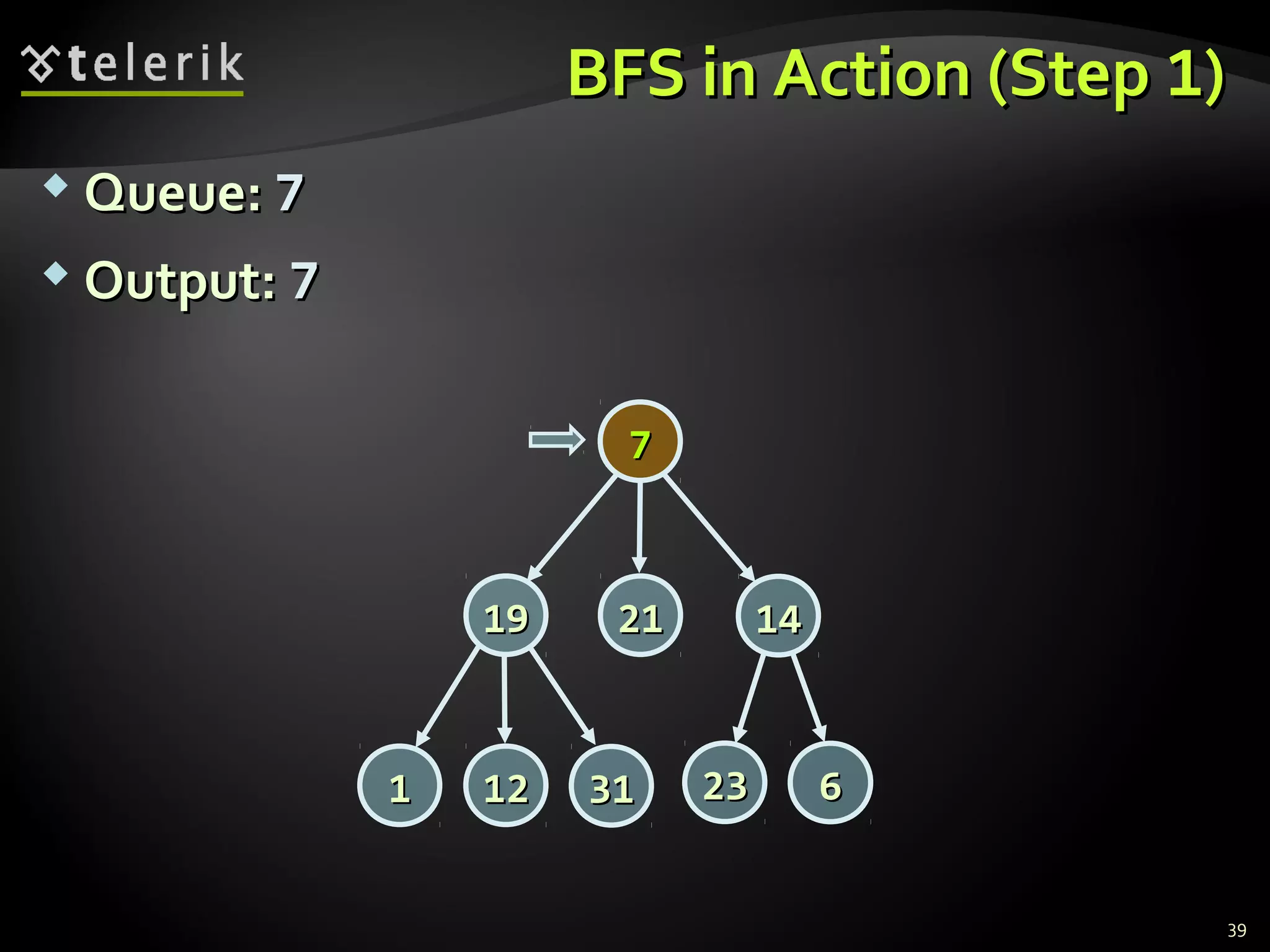
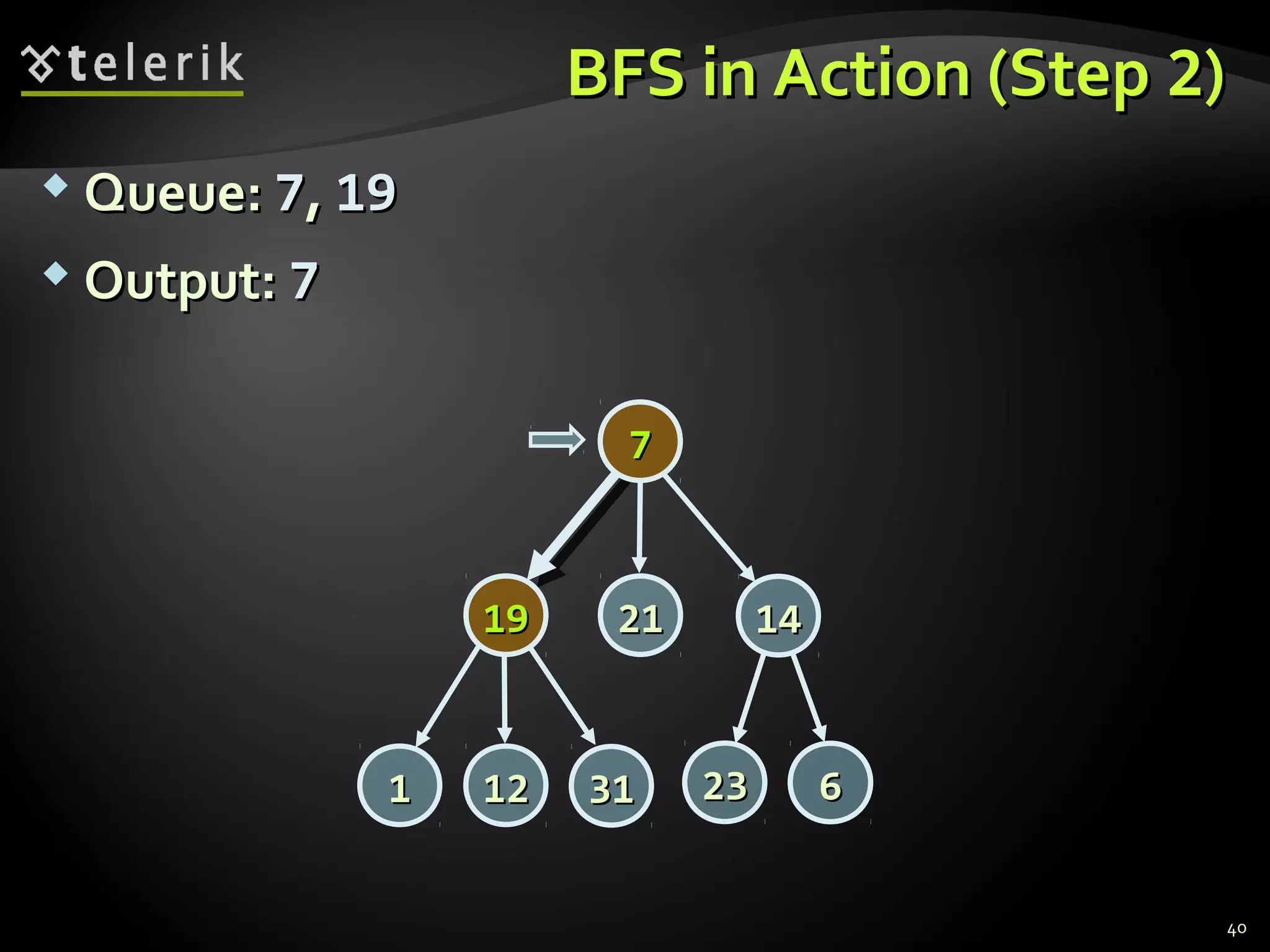
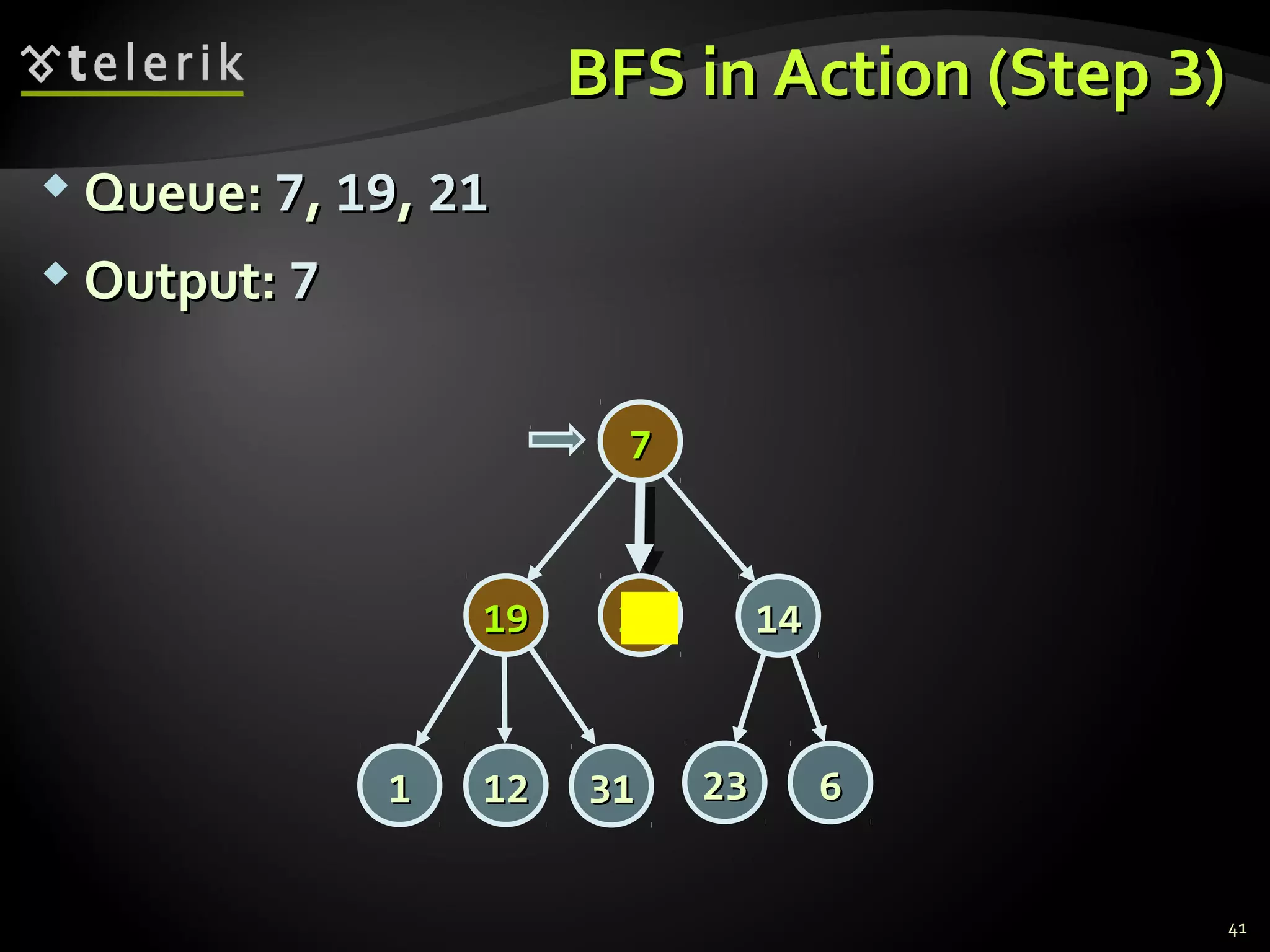
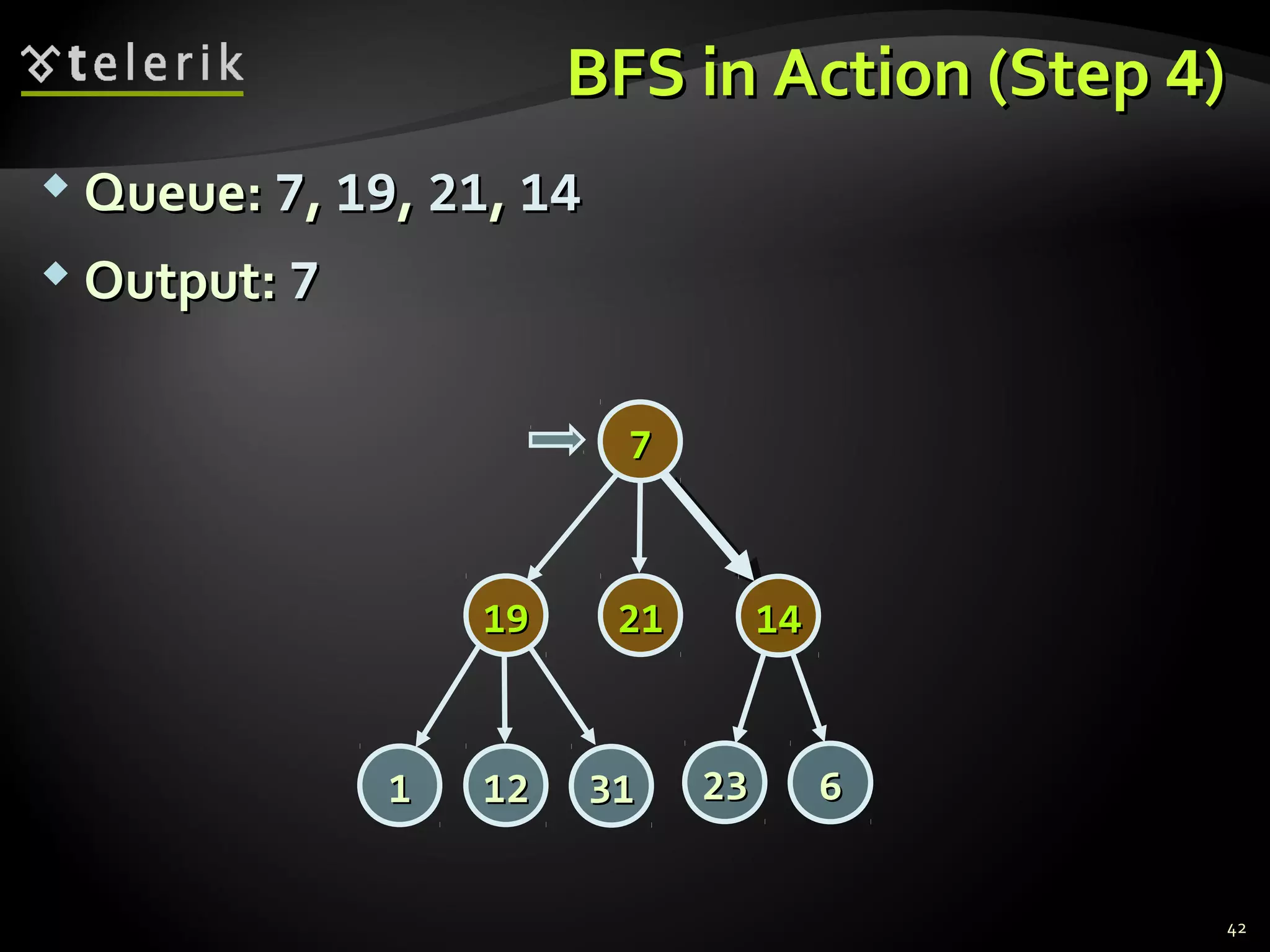
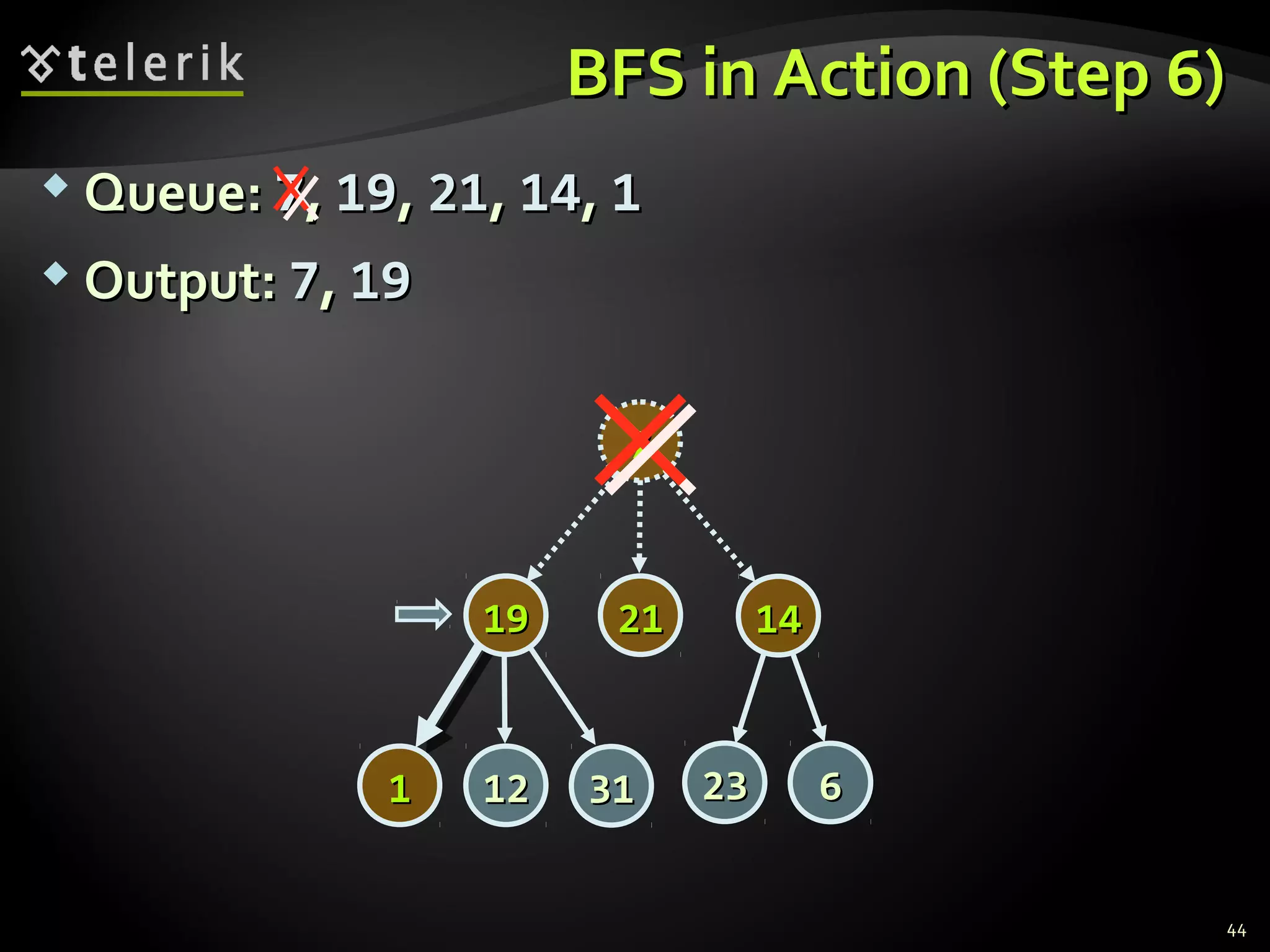
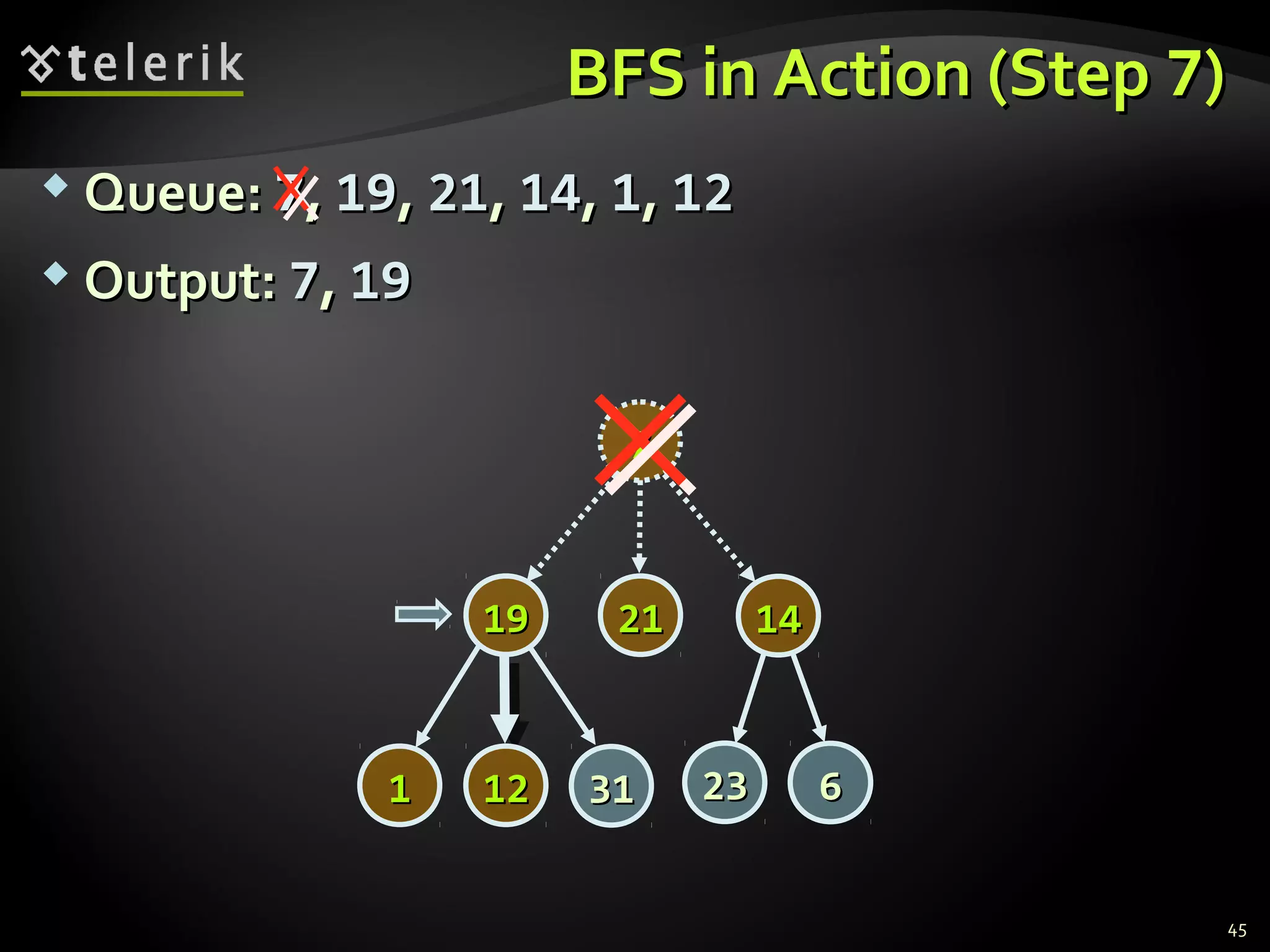
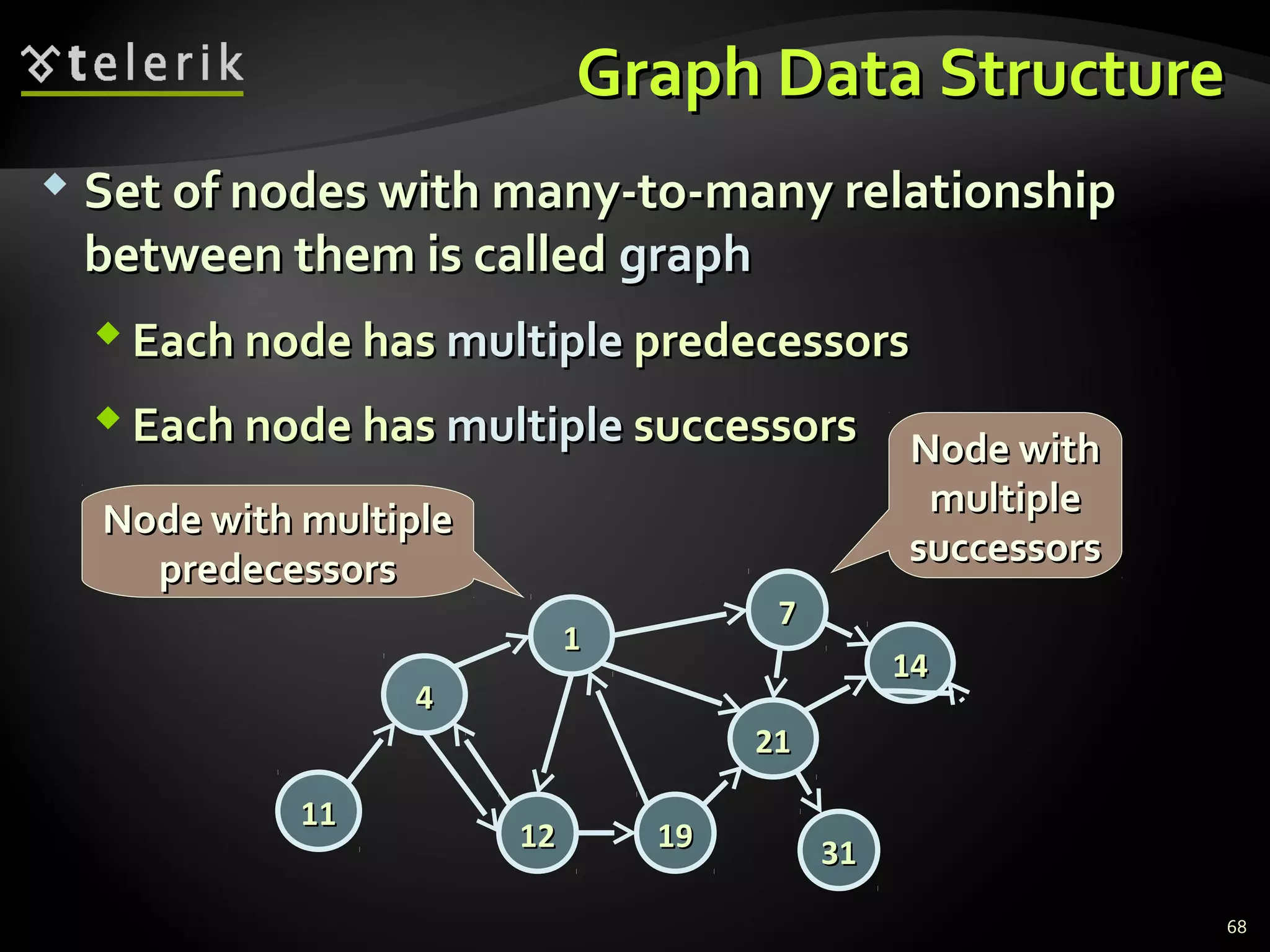
79. Graph Traversal AlgorithmsGraph Traversal Algorithms
 Depth-First Search (DFS) and Breadth-FirstDepth-First Search (DFS) and Breadth-First
Search (BFS) can traverse graphsSearch (BFS) can traverse graphs
 Each vertex should be is visited at most onceEach vertex should be is visited at most once
79
BFS(BFS(nodenode))
{{
queuequeue  nodenode
visited[visited[nodenode] = true] = true
while queue not emptywhile queue not empty
vv  queuequeue
printprint vv
for each childfor each child cc ofof vv
if not visited[if not visited[cc]]
queuequeue  cc
visited[visited[cc] = true] = true
}}
DFS(DFS(nodenode))
{{
stackstack  nodenode
visited[visited[nodenode] = true] = true
while stack not emptywhile stack not empty
vv  stackstack
printprint vv
for each childfor each child cc ofof vv
if not visited[if not visited[cc]]
stackstack  cc
visited[visited[cc] = true] = true
}}

80. Recursive DFS Graph TraversalRecursive DFS Graph Traversal
80
void TraverseDFSRecursive(node)void TraverseDFSRecursive(node)
{{
if (not visited[node])if (not visited[node])
{{
visited[node] = truevisited[node] = true
print nodeprint node
foreach child nodeforeach child node cc of nodeof node
{{
TraverseDFSRecursive(TraverseDFSRecursive(cc););
}}
}}
}}
vois Main()vois Main()
{{
TraverseDFS(firstNode);TraverseDFS(firstNode);
}}

81. Graphs andTraversalsGraphs andTraversals
Live DemoLive Demo

82. SummarySummary
 Trees are recursive data structure – node with setTrees are recursive data structure – node with set
of children which are also nodesof children which are also nodes
 Binary Search Trees are ordered binary treesBinary Search Trees are ordered binary trees
 Balanced trees have weight of log(n)Balanced trees have weight of log(n)
 Graphs are sets of nodes with many-to-manyGraphs are sets of nodes with many-to-many
relationship between themrelationship between them
 Can be directed/undirected, weighted /Can be directed/undirected, weighted /
unweighted, connected / not connected, etc.unweighted, connected / not connected, etc.
 Tree / graph traversals can be done by Depth-FirstTree / graph traversals can be done by Depth-First
Search (DFS) and Breadth-First Search (BFS)Search (DFS) and Breadth-First Search (BFS)
82

83. Trees and GraphsTrees and Graphs
Questions?Questions?
http://academy.telerik.com

84. ExercisesExercises
1.1. Write a program to traverse the directoryWrite a program to traverse the directory
C:WINDOWSC:WINDOWS and all its subdirectories recursively andand all its subdirectories recursively and
to display all files matching the maskto display all files matching the mask *.exe*.exe. Use the. Use the
classclass System.IO.DirectorySystem.IO.Directory..
2.2. Define classesDefine classes FileFile {{ stringstring name,name, intint sizesize }} andand
FolderFolder {{ stringstring name,name, File[] filesFile[] files,, Folder[]Folder[]
childFolderschildFolders }} and using them build a tree keepingand using them build a tree keeping
all files and folders on the hard drive starting fromall files and folders on the hard drive starting from
C:WINDOWSC:WINDOWS. Implement a method that calculates. Implement a method that calculates
the sum of the file sizes in given subtree of the treethe sum of the file sizes in given subtree of the tree
and test it accordingly. Use recursive DFS traversal.and test it accordingly. Use recursive DFS traversal.
84

85. Exercises (2)Exercises (2)
3.3. Implement the recursive Depth-First-Search (DFS)Implement the recursive Depth-First-Search (DFS)
traversal algorithm. Test it with the sample graphtraversal algorithm. Test it with the sample graph
from the demonstrations.from the demonstrations.
4.4. Implement the queue-based Breath-First-SearchImplement the queue-based Breath-First-Search
(BFS) traversal algorithm. Test it with the sample(BFS) traversal algorithm. Test it with the sample
graph from the demonstrations.graph from the demonstrations.
5.5. Write a program for finding all cycles in givenWrite a program for finding all cycles in given
undirected graph using recursive DFS.undirected graph using recursive DFS.
6.6. Write a program for finding all connectedWrite a program for finding all connected
components of given undirected graph. Use acomponents of given undirected graph. Use a
sequence of DFS traversals.sequence of DFS traversals.
85

86. Exercises (3)Exercises (3)
7.7. Write a program for finding the shortest pathWrite a program for finding the shortest path
between two vertices in a weighted directed graph.between two vertices in a weighted directed graph.
Hint: Use theHint: Use the Dijkstra's algorithmDijkstra's algorithm..
8.8. We are given a set of N tasks that should beWe are given a set of N tasks that should be
executed in a sequence. Some of the tasks dependexecuted in a sequence. Some of the tasks depend
on other tasks. We are given a list of tasks { ton other tasks. We are given a list of tasks { tii, t, tjj}}
where twhere tjj depends on the result of tdepends on the result of tii and should beand should be
executed after it. Write a program that arranges theexecuted after it. Write a program that arranges the
tasks in a sequence so that each task depending ontasks in a sequence so that each task depending on
another task is executed after it. If suchanother task is executed after it. If such
arrangement is impossible indicate this fact.arrangement is impossible indicate this fact.
Example: {Example: {11,, 22}, {}, {22,, 55}, {}, {22,, 44}, {}, {33,, 11}}  33,, 11,, 22,, 55,, 44 86