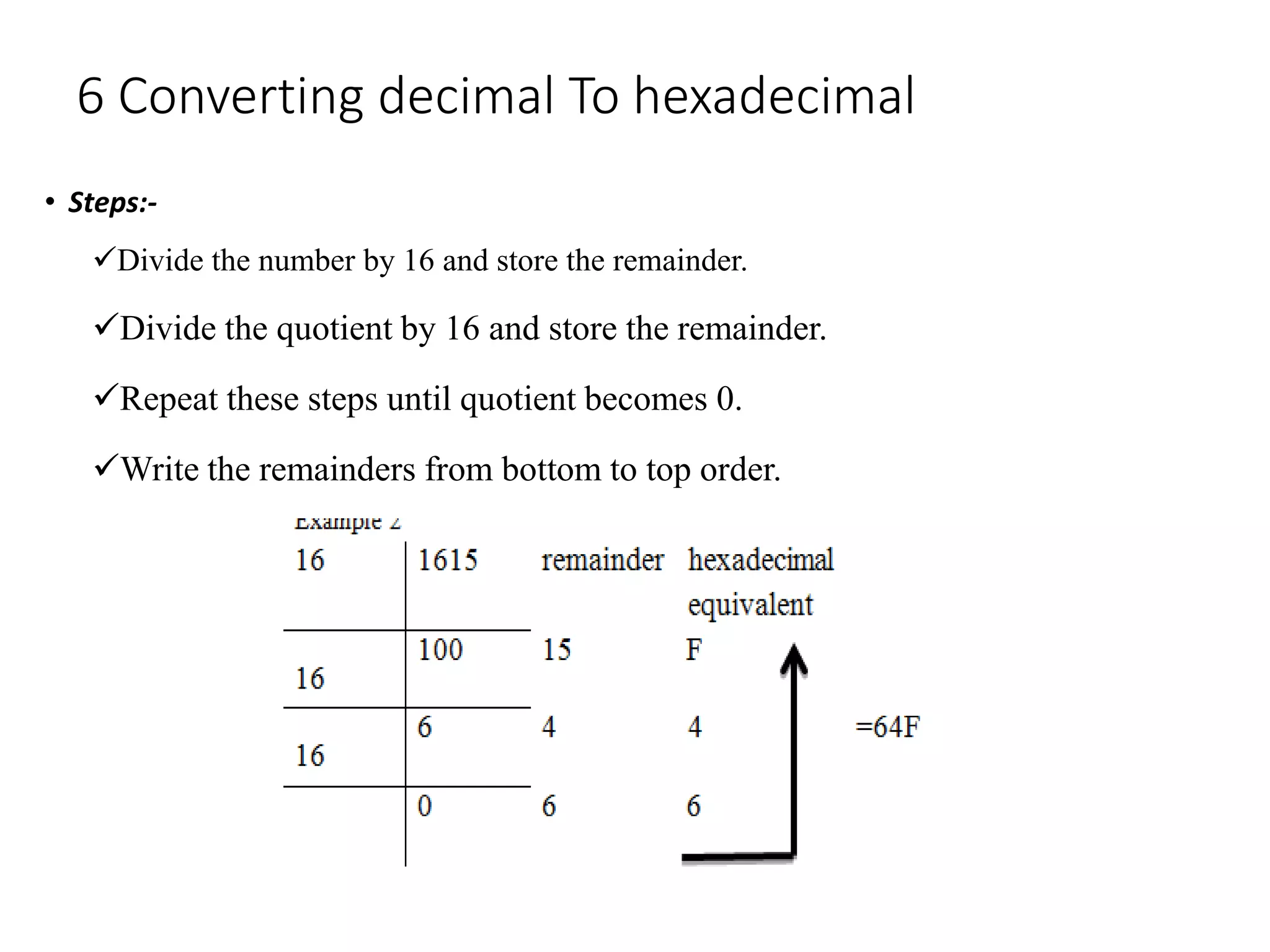
This document discusses various data representation systems used in computers, including: - Binary, decimal, hexadecimal, and octal number systems. Binary uses two digits (0,1) while other systems use bases of 10, 16, and 8 respectively. - Units of data representation such as bits, bytes, kilobytes, megabytes and gigabytes which are used to measure computer storage. - Methods for converting between number systems, including dividing numbers into place values and multiplying digits by their place values. - Special codes like Binary Coded Decimal (BCD) which represents each decimal digit with 4 binary bits. - Binary arithmetic operations and how addition works the same in any number system by following

1. METTU UNIVERSITY
Department of health informatics
Chapter three:
Data representation in computers

2. Contents to be covered
Units of data representation
Types of numbering system
Conversion from one base to another
Binary arithmetic operation
Non numeric code

3. Units of data representation
Computers speak binary. Binary language consists of combinations
of 1's and 0's that represent characters of other languages (in our
case the English language)
One digit in binary number system is called bit and combination
of eight bits is called a byte.
Byte is the basic unit that is used to represent the alphabetic and
numeric data.

4. Cont…
Kilobytes, Megabytes, and Gigabyte
Eight bits are known as a byte.
1,000 bytes = 1 kilobyte
(1,000 characters = 1 kilobyte)
1,000,000 bytes = 1 megabyte
(1,000,000 characters = 1 megabyte)
1,000,000,000 bytes = 1 gigabyte
(1 gigabyte= 1,000,000,000 characters)

5. Number system
1. Hexadecimal number system, here we have 16 possibilities (“0,
1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, and f”). The base or radix of
hexadecimal number system is 16.

6. Binary number system
Digital systems and computers use the Binary system because it has only two states
(0 and 1). The base or radix of binary system is 2.
A number in the Binary system is expressed by the following expression:
Examples:
• (1011)2 = (1X2
3
)+(0X2
2
)+(1X2
1
)+(1X2
0
) = 8+0+2+1= (11)10
• (10110)2 = (1X2
4
)+(0X2
3
)+(1X2
2
)+(1X2
1
)+(0X2
0
) = 16+0+4+2+0= (22)10
• (101100)2=(1X2
5
)+(0X2
4
)+(1X2
3
)+(1X2
2
)+(0X2
1
)+(0X2
0
)=32+0+8+4+0+0=(44)10
(dndn-1…d1d0)2 = (dnX2n
)+ (dn-1X2n-1
)+…+ (d1X21
)+(d0X20
)
Where d = {0,1}

7. 7
The Binary Numbering System (Cont.)
A binary digit is called the BIT (BInary digiT).
A group of eight bits is called the BYTE.
The leftmost bit of a number is called the Most Significant Bit.
The rightmost bit of a number is called the Least Significant Bit.
A binary system with N bits can represent the numbers from
0 to 2
N
-1.
In a binary system with N digits there are 2
N
different
combinations.
A binary number is multiplied by two, if we append a zero at the
least significant Bit.
Powers of 2:
2
0
= 1
2
1
= 2
2
2
= 4
2
3
= 8
2
4
= 16
2
5
= 32
2
6
= 64
2
7
= 128
2
8
= 256
2
9
= 512
2
10
=1024=1K
2
16
= 65536

8. 2. Decimal number system
In the Decimal system a digit can take one out of ten different values (0..9).
Has 10 possibilities
A number in the decimal system is expressed by the following expression:
• Notes:
A decimal system with N digits can represent the numbers from 0 to 10
N
-1.
In a decimal system with N digits there are 10
N
different combinations.
The digit to the right of a number is called the Least Significant Digit (LSD).
The digit to the left of a number is called the Most Significant Digit (MSD).
(dndn-1…d1d0)10 = (dnX10n
)+ (dn-1X10n-1
)+…+ (d1X101
)+(d0X100
)
Where d = {0,1,2,3,4,5,6,7,8,9} = {0..9}

9. 9
3. Octal and Hexadecimal Numbering Systems
Computers use the binary system to represent data. In most cases a number is represented
with 16, 32 or more bits, which is difficult to be handled by humans.
To make binary numbers easier to manipulate, we can group the bits of the number in
groups of 2, 3 or 4 bits.
If we take a group of 2 bits, then we can have 4 combinations or different digits in each
group. Thus the new system is a system with the base of 4.
e.g. (10110100)2= (10 11 01 00)2= (2310)4
The system with the base 4 is not widely used because many digits are still required to
represent typical numbers.
(11)2 = 3 (00)2 = 0

10. 10
The Octal and Hexadecimal Numbering Systems (Cont.)
If we take a group of 3 bits, then we can have 8 combinations or different digits in
each group. The new system is a system with the base of 8 called Octal system.
e.g. (10110100)2= (10 110 100)2= (264)8
If we take a group of 4 bits, then we can have 16 combinations or different digits in
each group. The new system is a system with the base of 16 called hexadecimal or
hex system. Letters A to F are used to represent digits from 10 to 15.
e.g. (10110100)2= (1011 0100)2= (B4)16
(110)2 = 6

11. 11
Decimal, Binary, Octal and Hexadecimal Conversion Table
Decimal Binary Base 4 Octal Hex
0 0000 0 0 0
1 0001 1 1 1
2 0010 2 2 2
3 0011 3 3 3
4 0100 10 4 4
5 0101 11 5 5
6 0110 12 6 6
7 0111 13 7 7
8 1000 20 10 8
9 1001 21 11 9
10 1010 22 12 A
11 1011 23 13 B
12 1100 30 14 C
13 1101 31 15 D
14 1110 32 16 E
15 1111 33 17 F

12. Conversion System from One base to another
 To convert numbers from one system to another. the following conversions will
be considered.
 Converting between binary and decimal numbers.
 Converting octal numbers to decimal and binary form.
 Converting hexadecimal numbers to decimal and binary form.

13. 1 Converting binary numbers to decimal numbers
 To convert a binary number to a decimal number, we proceed as follows:
First, write the place values starting from the right hand side.
The place value of a digit in a number refers to the position of the digit in
that number i.e. whether; tens, hundreds, thousands etc.
Write each digit under its place value.
Multiply each digit by 2 power of its corresponding place value.
Add up the products. The answer will be the decimal number in base ten.
EXAMPLE: Convert 1011012 to base 10(or decimal) number

14. Cont…
 Solution
 Multiply each digit by its place value
N10=(1*25) +(0*24)+(1*23)+(1*22)+(0*21)+(1*20)
N10=32+0+8+4+0+1
=4510
Place value 25 24 23 22 21 20
Binary digits 1 0 1 1 0 1

15. Exercise
 Convert each of the following binary numbers to decimal number
100001
11100
0011
111111

16. 2 Converting octal to decimal
 To convert a octal to a decimal number, we proceed as follows:
First, write the place values starting from the right hand side.
Write each digit under its place value.
Multiply each digit by its corresponding place value.
Add up the products. The answer will be the decimal number in base ten.
• EXAMPLE: Convert (137)8 to it decimal or base 10

17. Cont….
 Solution
= 1×82+3×81+7×80
= 64+24+7
=(95)10
Place value 82 81 80
Octal digit 1 3 7
Multiply each digit by its place value

18. Exercise
 Convert each of the following octal numbers to decimal number
(7014)8=(-----)10
(724)8 =(-----)10
(1923)8 =(-----)10

19. 3 Converting hexadecimal to decimal
 To convert a hexadecimal to a decimal number, we proceed as
follows:
First, write the place values starting from the right hand side.
Write each digit under its place value.
Multiply each digit by its corresponding place value.
Add up the products. The answer will be the decimal number in base
ten.
• EXAMPLE: Convert (ABC)16 to it decimal or base 10

20. Cont…
 Solution
 (ABC)16 => C x 160 = 12 x 1 = 12 +
B x 161 = 11 x 16 = 176+
A x 162 = 10 x 256 = 2560
= (2748)10
Place value 16 2 16 1 16 0
Hexad digit A B C
Multiply each digit by its place value

21. Exercise
 Convert each of the following hexadecimal numbers to decimal number
(7D)16= (….)10
(13F)16 = (….)10
(3AE)16= (….)10

22. 4 Converting decimal To binary
Conversion steps:
Divide the number by 2 and store the remainder.
Divide the quotient by 2 and store the remainder.
Repeat these steps until quotient becomes 0.
Write the remainders from bottom to top order

23. Cont …

24. Exercise
 Convert each of the following decimal number to binary number
• 17410 = --------2
• 25010 = --------2

25. 5 Converting decimal To octal
• Steps
Divide the number by 8 and store the remainder.
Divide the quotient by 8 and store the remainder.
Repeat these steps until quotient becomes 0.
Write the remainders from bottom to top order.

26. Exercise
 Convert each of the following decimal number to octal number
(1792)10=()8
(127)10 = ()8
(52)10 = ()8

27. 6 Converting decimal To hexadecimal
• Steps:-
Divide the number by 16 and store the remainder.
Divide the quotient by 16 and store the remainder.
Repeat these steps until quotient becomes 0.
Write the remainders from bottom to top order.

28. Exercise
 Convert each of the following decimal number to hexadecimal number
 (540)10=(21C)16
 (7562)10 = (1D8A)16

29. 7 Converting binary to octal
 Step:-
Divide the binary number into groups of three bits each beginning from right side
Add 0s to the left, if last group is incomplete.
Convert each group into decimal.
• Example convert (10101111)2= ( ) 8
=10,101,111
=010,101,111
=2 3 7
(10101111)2= (237)8

30. Exercise
 Convert each of the following binary to octal number
(1010101)2=1258
(01101)2= (13)8
(1011010111)2 = (1327)8

31. 8. Converting binary to hexadecimal
Step:
 Divide the binary number into groups to four bits each beginner from
the right side.
 Add to left, it is the last group is in compute
 Convert each group into decimal
E.g. (110101)16= ( ) 16
=0011 0101
=3 5
= (35)16

32. Exercise
 Convert each of the following binary to hexadecimal number
(111101110101011)2= (F7BC) 16
(1010111011)2 = (2BB)16

33. 9. Converting Octal to binary
1. Convert each digit to octal number it equivalent three to its equivalent
three digit binary numbers all the binary group into a single groups.
2. Combine all the binary groups into a single group.
E.g. (53)8 = ( )2
(53) = 5 3
= 101 011
=(101011)2

34. Exercise
 Convert each of the following octal to binary number
(705)8 = (111000101)2
128 = (001 010)2

35. 10 . Converting Octal to hexadecimal
 Octal-to-binary and then to-hexadecimal
Example: convert (1076)8 to hexadecimal
Soln. To binary => ( 001000111110)
then
To hexa-decimal => (23E)

36. 36
The Binary Coded Decimal (BCD) System
 In many applications it is required to encode each decimal digit to the equivalent 4-
bit binary number. This binary code is called the BCD code.
E.g. (2 4 9)10= (0010 0100 1001)BCD
Exercise:
(173)10 = (?)2 = (?)BCD
(1000 0111)BCD = (?)10
(0100 0010)2 = (?)BCD
(53)16 = (?)BCD
(1011 0101)BCD = (?)10
4 =(0100)2

37. 37
Addition in any numbering system
 Addition in any numbering system can be performed by following the same rules used for
decimal addition, where 10 is replaced by the base of the system (R).
Decimal Addition:
7 4 3 +
1 8 6
9 2 9
 Rules for addition in the decimal system:
Begin the addition by adding the 2 least significant digits first.
Perform the integer division of the sum with 10. Write down the remainder of the division
and carry out the result to the next column.
Repeat the addition for the next columns by adding the two digits and the carry from the
previous column.
1+ 7 + 1 = 9  9/10 = 0 + 9/10  write 9 and carry 0
3 + 6 = 9  9/10 = 0 + 9/10  write 9 and carry 0
8 + 4 = 12  12/10 = 1 + 2/10  write 2 and carry 1

38. ACOE161 38
Exercise: Perform the following additions
(173)8+ (265)8 = (?)8
(01101011)2+ (00111010)2 = (?)2
(1243)5+ (234)5 = (?)5
(1A79)16+ (C827)16 = (?)16
(1A79)18+ (C827)18 = (?)18

39. 39
Subtraction in any numbering system
 Subtraction in any numbering system can be performed by following the same rules
used for decimal addition, where 10 is replaced by the base of the system (R).
7 4 9 -
1 8 6
5 6 3
 Rules for subtraction in the decimal system:
Begin the subtraction from 2 least significant digits first.
If the minuend is greater than the subtrahend then perform the subtraction.
If the minuend is less than the subtrahend then borrow 1 from the next column.
Write down the result of (minuend + 10 - subtrahend). The one borrowed must be
subtracted from the minuend of the next column.
Repeat the subtraction for the next columns.
(7-11)  7 - 1 - 1 = 5 write 5 and borrow 0 from next column
(96)  9 - 6 = 3  write 3 and borrow 0 from next column
(4<8)  borrow 1  10+4-8=6  write 6 and borrow 1 from next column

40. ACOE161 40
Exercise: Perform the following subtractions
(476)10 - (285)10 = (?)10
(285)10 - (476)10 = (?)10
(173)8 - (265)8 = (?)8
(01101001)2- (00111010)2 = (?)2
(423)5 - (234)5 = (?)5
(61A9)16- (C827)16 = (?)16
(61A9)18- (C827)18 = (?)18

41. ACOE161 41
Non-numeric codes
Not all information processed by computer systems are numbers
Computers process also text, images, speech, video etc.
This information must also be represented in the computer using
binary signals
Non-numerical information is represented using a code

42. Quiz
1. What is byte?
2. Convert (2798)10 to octal and hexadecimal number
system respectively
3. Convert (1010101010101)2 to octal and hexadecimal
number system respectively?