Recursion allows a method to call itself, either directly or indirectly. The document discusses examples of calculating factorials and generating all 0/1 vectors recursively. It also describes an algorithm to find all paths from the start to end of a labyrinth recursively by exploring neighbor cells. Recursion can be harmful if it leads to excessive memory usage from redundant calculations; techniques like memoization can help address this. Overall, recursion is well-suited for combinatorial and other algorithms, but iteration may be preferable for problems that could result in inefficient recursion.

1. RecursionRecursion
The Power of Calling a Method from ItselfThe Power of Calling a Method from Itself
Svetlin NakovSvetlin Nakov
Telerik CorporationTelerik Corporation
www.telerik.comwww.telerik.com

2. Table of ContentsTable of Contents
1.1. What is Recursion?What is Recursion?
2.2. Calculating Factorial RecursivelyCalculating Factorial Recursively
3.3. Generating All 0/1 Vectors RecursivelyGenerating All 0/1 Vectors Recursively
4.4. Finding All Paths in a Labyrinth RecursivelyFinding All Paths in a Labyrinth Recursively
5.5. Recursion or Iteration?Recursion or Iteration?
2

3. What is Recursion?What is Recursion?
 RecursionRecursion is when a methods calls itselfis when a methods calls itself
Very powerful technique for implementingVery powerful technique for implementing
combinatorial and other algorithmscombinatorial and other algorithms
 Recursion should haveRecursion should have
Direct or indirect recursive callDirect or indirect recursive call
 The method calls itself directly or through otherThe method calls itself directly or through other
methodsmethods
Exit criteria (bottom)Exit criteria (bottom)
 Prevents infinite recursionPrevents infinite recursion
3

4. Recursive Factorial – ExampleRecursive Factorial – Example
 Recursive definition ofRecursive definition of n!n! ((n factorialn factorial):):
n! = n * (n–1)! for n >= 0n! = n * (n–1)! for n >= 0
0! = 10! = 1
5! = 5 * 4! = 5 * 4 * 3 * 2 * 1 * 1 = 1205! = 5 * 4! = 5 * 4 * 3 * 2 * 1 * 1 = 120
4! = 4 * 3! = 4 * 3 * 2 * 1 * 1 = 244! = 4 * 3! = 4 * 3 * 2 * 1 * 1 = 24
3! = 3 * 2! = 3 * 2 * 1 * 1 = 63! = 3 * 2! = 3 * 2 * 1 * 1 = 6
2! = 2 * 1! = 2 * 1 * 1 = 22! = 2 * 1! = 2 * 1 * 1 = 2
1! = 1 * 0! = 1 * 1 = 11! = 1 * 0! = 1 * 1 = 1
0! = 10! = 1
4

5. Recursive Factorial – ExampleRecursive Factorial – Example
 Calculating factorial:Calculating factorial:
00! =! = 11
n! = n* (n-1)!, n>0n! = n* (n-1)!, n>0
 Don't try this at home!Don't try this at home!
Use iteration insteadUse iteration instead
static decimal Factorial(decimal num)static decimal Factorial(decimal num)
{{
if (num == 0)if (num == 0)
return 1;return 1;
elseelse
return num * Factorial(num - 1);return num * Factorial(num - 1);
}}
The bottom ofThe bottom of
the recursionthe recursion
Recursive call: theRecursive call: the
method callsmethod calls
itselfitself 5

6. Recursive FactorialRecursive Factorial
Live DemoLive Demo

7. Generating 0/1 VectorsGenerating 0/1 Vectors
 How to generate all 8-bit vectors recursively?How to generate all 8-bit vectors recursively?
0000000000000000
0000000100000001
......
0111111101111111
1000000010000000
......
1111111011111110
1111111111111111
 How to generate all n-bit vectors?How to generate all n-bit vectors?
7

8.  AlgorithmAlgorithm Gen01(n)Gen01(n): put: put 00 andand 11 at the lastat the last
positionposition nn and calland call Gen01(n-1)Gen01(n-1) for the rest:for the rest:
Generating 0/1 Vectors (2)Generating 0/1 Vectors (2)
8
xx xx xx xx xx xx 00
Gen01(6):Gen01(6):
Gen01(5)Gen01(5)
xx xx xx xx xx xx 11
Gen01(5)Gen01(5)
xx xx xx xx xx 00 yy
Gen01(5):Gen01(5):
Gen01(4)Gen01(4)
xx xx xx xx xx 11 yy
Gen01(4)Gen01(4)
......
Gen01(-1)Gen01(-1)  Stop!Stop!

9. Generating 0/1 Vectors (3)Generating 0/1 Vectors (3)
static void Gen01(int index, int[] vector)static void Gen01(int index, int[] vector)
{{
if (index == -1)if (index == -1)
Print(vector);Print(vector);
elseelse
for (int i=0; i<=1; i++)for (int i=0; i<=1; i++)
{{
vector[index] = i;vector[index] = i;
Gen01(index-1, vector);Gen01(index-1, vector);
}}
}}
static void Main()static void Main()
{{
int size = 8;int size = 8;
int[] vector = new int[size];int[] vector = new int[size];
Gen01(size-1, vector);Gen01(size-1, vector);
}}
9

10. Generating 0/1VectorsGenerating 0/1Vectors
Live DemoLive Demo

11. Finding All Paths in a LabyrinthFinding All Paths in a Labyrinth
 We are given a labyrinthWe are given a labyrinth
Represented as matrix of cells of size M x NRepresented as matrix of cells of size M x N
Empty cells are passable, the others (*) are notEmpty cells are passable, the others (*) are not
 We start from the top left corner and can moveWe start from the top left corner and can move
in the allin the all 44 directions: left, right, up, downdirections: left, right, up, down
 We need to find all paths to the bottom rightWe need to find all paths to the bottom right
cornercorner
11
StartStart
positionposition EndEnd
positionposition
**
** ** ** **
** ** ** ** **

12. Finding All Paths in a Labyrinth (2)Finding All Paths in a Labyrinth (2)
 There are 3 different paths from the top leftThere are 3 different paths from the top left
corner to the bottom right corner:corner to the bottom right corner:
12
00 11 22 **
** ** 33 ** **
66 55 44
77 ** ** ** ** **
88 99 1010 1111 1212 1313 1414
00 11 22 ** 88 99 1010
** ** 33 ** 77 ** 1111
44 55 66 1212
** ** ** ** ** 1313
1414
1) 2)
00 11 22 **
** ** 33 ** **
44 55 66 77 88
** ** ** ** ** 99
1010
3)

13. Finding All Paths in a Labyrinth (2)Finding All Paths in a Labyrinth (2)
 Suppose we have an algorithmSuppose we have an algorithm FindExit(x,y)FindExit(x,y)
that finds and prints all paths to the exit (bottomthat finds and prints all paths to the exit (bottom
right corner) starting from positionright corner) starting from position (x,y)(x,y)
 IfIf (x,y)(x,y) is not passable, no paths are foundis not passable, no paths are found
 IfIf (x,y)(x,y) is already visited, no paths are foundis already visited, no paths are found
 Otherwise:Otherwise:
 Mark positionMark position (x,y)(x,y) as visited (to avoid cycles)as visited (to avoid cycles)
 Find all paths to the exit from all neighbor cells:Find all paths to the exit from all neighbor cells:
(x-1,y)(x-1,y) ,, (x+1,y)(x+1,y) ,, (x,y+1)(x,y+1) ,, (x,y-1)(x,y-1)
 Mark positionMark position (x,y)(x,y) as free (can be visited again)as free (can be visited again)
13

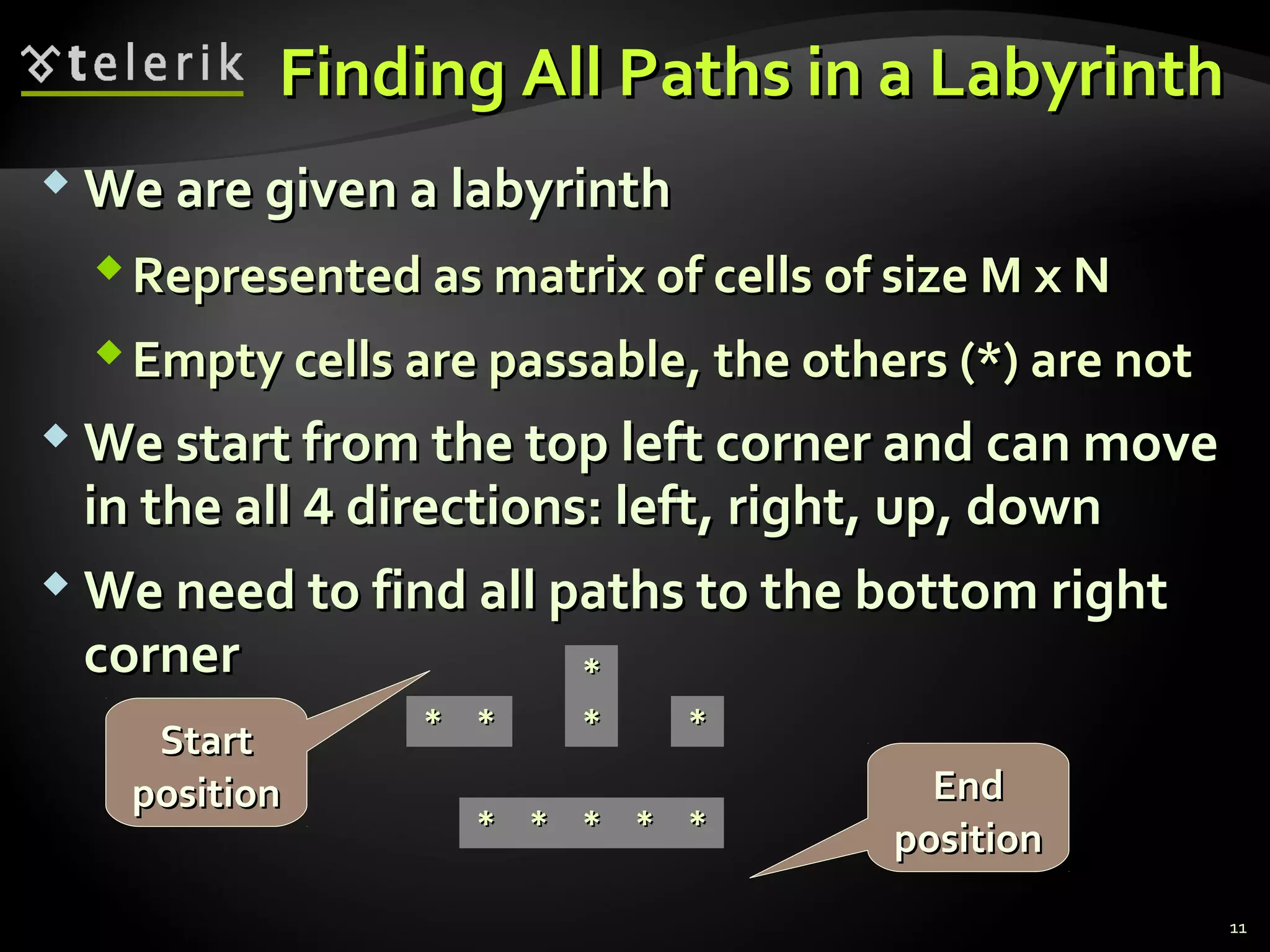
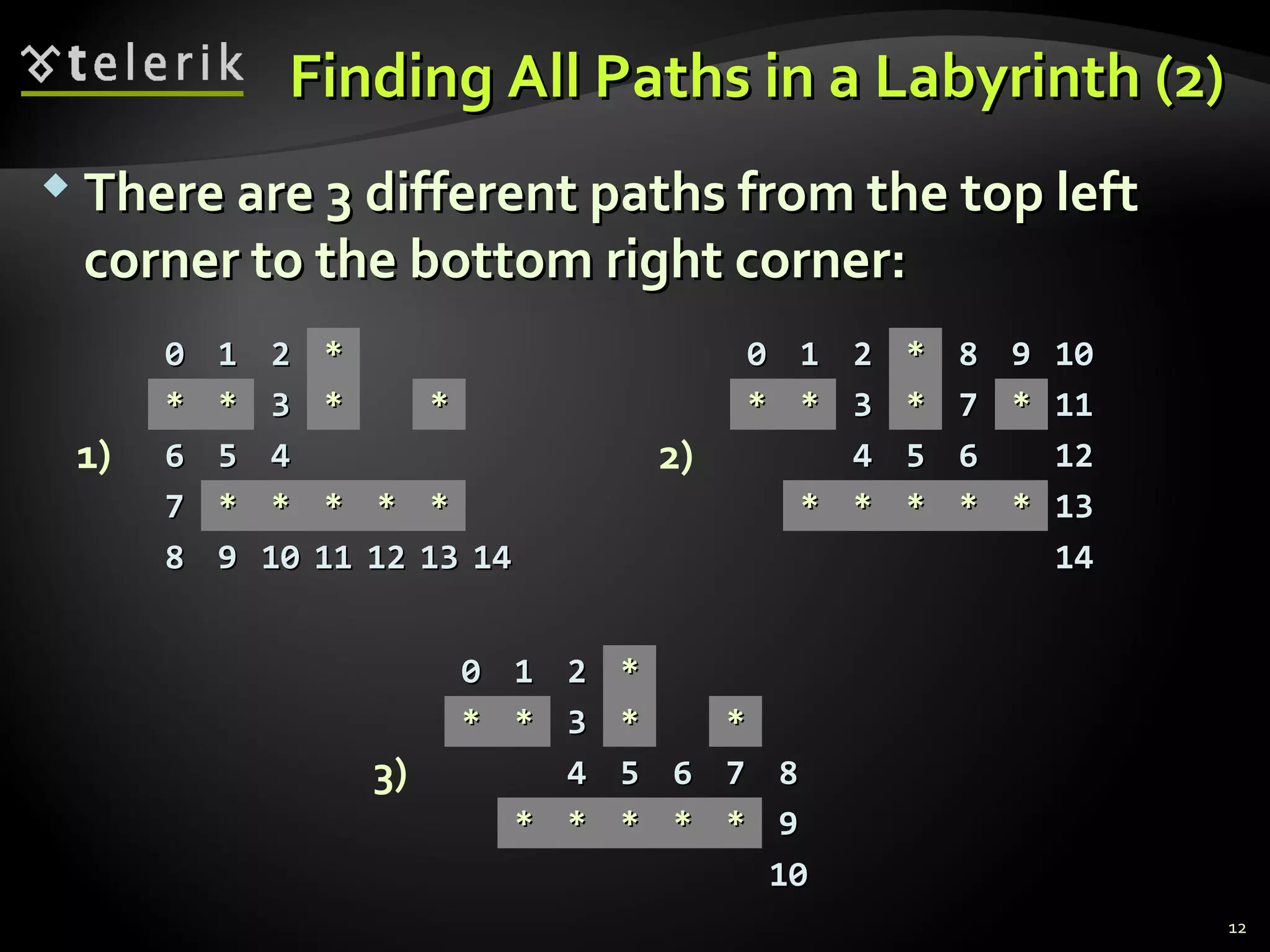
14.  Representing the labyrinth as matrix of charactersRepresenting the labyrinth as matrix of characters
(in this example(in this example 55 rows androws and 77 columns):columns):
 Spaces ('Spaces (' ') are passable cells') are passable cells
 Asterisks ('Asterisks ('**') are not passable cells') are not passable cells
 The symbol 'The symbol 'ee' is the exit (can be multiple)' is the exit (can be multiple)
Find All Paths: AlgorithmFind All Paths: Algorithm
14
static char[,] lab =static char[,] lab =
{{
{' ', ' ', ' ', '*', ' ', ' ', ' '},{' ', ' ', ' ', '*', ' ', ' ', ' '},
{'*', '*', ' ', '*', ' ', '*', ' '},{'*', '*', ' ', '*', ' ', '*', ' '},
{' ', ' ', ' ', ' ', ' ', ' ', ' '},{' ', ' ', ' ', ' ', ' ', ' ', ' '},
{' ', '*', '*', '*', '*', '*', ' '},{' ', '*', '*', '*', '*', '*', ' '},
{' ', ' ', ' ', ' ', ' ', ' ', 'е'},{' ', ' ', ' ', ' ', ' ', ' ', 'е'},
};};

15. Find All Paths: Algorithm (2)Find All Paths: Algorithm (2)
15
static void FindExit(int row, int col)static void FindExit(int row, int col)
{{
if ((col < 0) || (row < 0) || (col >= lab.GetLength(1))if ((col < 0) || (row < 0) || (col >= lab.GetLength(1))
|| (row >= lab.GetLength(0)))|| (row >= lab.GetLength(0)))
{{
// We are out of the labyrinth -> can't find a path// We are out of the labyrinth -> can't find a path
return;return;
}}
// Check if we have found the exit// Check if we have found the exit
if (lab[row, col] == 'е')if (lab[row, col] == 'е')
{{
Console.WriteLine("Found the exit!");Console.WriteLine("Found the exit!");
}}
if (lab[row, col] != ' ')if (lab[row, col] != ' ')
{{
// The current cell is not free -> can't find a path// The current cell is not free -> can't find a path
return;return;
}} (example continues)(example continues)

16. Find All Paths: Algorithm (3)Find All Paths: Algorithm (3)
16
// Temporary mark the current cell as visited// Temporary mark the current cell as visited
lab[row, col] = 's';lab[row, col] = 's';
// Invoke recursion the explore all possible directions// Invoke recursion the explore all possible directions
FindExit(row, col-1); // leftFindExit(row, col-1); // left
FindExit(row-1, col); // upFindExit(row-1, col); // up
FindExit(row, col+1); // rightFindExit(row, col+1); // right
FindExit(row+1, col); // downFindExit(row+1, col); // down
// Mark back the current cell as free// Mark back the current cell as free
lab[row, col] = ' ';lab[row, col] = ' ';
}}
static void Main()static void Main()
{{
FindExit(0, 0);FindExit(0, 0);
}}

17. Find All Paths in a LabyrinthFind All Paths in a Labyrinth
Live DemoLive Demo

18.  How to print all paths found by our recursiveHow to print all paths found by our recursive
algorithm?algorithm?
Each move's direction can be stored in arrayEach move's direction can be stored in array
Need to pass the movement direction at eachNeed to pass the movement direction at each
recursive callrecursive call
At the start of each recursive call the currentAt the start of each recursive call the current
direction is appended to the arraydirection is appended to the array
At the end of each recursive call the lastAt the end of each recursive call the last
direction is removed form the arraydirection is removed form the array
Find All Paths and Print ThemFind All Paths and Print Them
18
static char[] path =static char[] path =
new char[lab.GetLength(0) * lab.GetLength(1)];new char[lab.GetLength(0) * lab.GetLength(1)];
static int position = 0;static int position = 0;

19. Find All Paths and Print Them (2)Find All Paths and Print Them (2)
19
static void FindPathToExit(int row, int col, char direction)static void FindPathToExit(int row, int col, char direction)
{{
......
// Append the current direction to the path// Append the current direction to the path
path[position++] = direction;path[position++] = direction;
if (lab[row, col] == 'е')if (lab[row, col] == 'е')
{{
// The exit is found -> print the current path// The exit is found -> print the current path
}}
......
// Recursively explore all possible directions// Recursively explore all possible directions
FindPathToExit(row, col - 1, 'L'); // leftFindPathToExit(row, col - 1, 'L'); // left
FindPathToExit(row - 1, col, 'U'); // upFindPathToExit(row - 1, col, 'U'); // up
FindPathToExit(row, col + 1, 'R'); // rightFindPathToExit(row, col + 1, 'R'); // right
FindPathToExit(row + 1, col, 'D'); // downFindPathToExit(row + 1, col, 'D'); // down
......
// Remove the last direction from the path// Remove the last direction from the path
position--;position--;
}}

20. Find and Print AllFind and Print All
Paths in a LabyrinthPaths in a Labyrinth
Live DemoLive Demo

21. Recursion or Iteration?Recursion or Iteration?
When to Use andWhen to Avoid Recursion?When to Use andWhen to Avoid Recursion?

22. Recursion Can be Harmful!Recursion Can be Harmful!
 When used incorrectly the recursion could takeWhen used incorrectly the recursion could take
too much memory and computing powertoo much memory and computing power
 Example:Example:
static decimal Fibonacci(int n)static decimal Fibonacci(int n)
{{
if ((n == 1) || (n == 2))if ((n == 1) || (n == 2))
return 1;return 1;
elseelse
return Fibonacci(n - 1) + Fibonacci(n - 2);return Fibonacci(n - 1) + Fibonacci(n - 2);
}}
static void Main()static void Main()
{{
Console.WriteLine(Fibonacci(10)); // 89Console.WriteLine(Fibonacci(10)); // 89
Console.WriteLine(Fibonacci(50)); // This will hang!Console.WriteLine(Fibonacci(50)); // This will hang!
}}
22

23. Harmful RecursionHarmful Recursion
Live DemoLive Demo

24. How the Recursive FibonacciHow the Recursive Fibonacci
Calculation Works?Calculation Works?
24
 fib(n) makes about fib(n) recursive callsfib(n) makes about fib(n) recursive calls
 The same value is calculated many, many times!The same value is calculated many, many times!

25. Fast Recursive FibonacciFast Recursive Fibonacci
 Each Fibonacci sequence member can beEach Fibonacci sequence member can be
remembered once it is calculatedremembered once it is calculated
Can be returned directly when needed againCan be returned directly when needed again
25
static decimal[] fib = new decimal[MAX_FIB];static decimal[] fib = new decimal[MAX_FIB];
static decimal Fibonacci(int n)static decimal Fibonacci(int n)
{{
if (fib[n] == 0)if (fib[n] == 0)
{{
// The value of fib[n] is still not calculated// The value of fib[n] is still not calculated
if ((n == 1) || (n == 2))if ((n == 1) || (n == 2))
fib[n] = 1;fib[n] = 1;
elseelse
fib[n] = Fibonacci(n - 1) + Fibonacci(n - 2);fib[n] = Fibonacci(n - 1) + Fibonacci(n - 2);
}}
return fib[n];return fib[n];
}}

26. Fast Recursive FibonacciFast Recursive Fibonacci
Live DemoLive Demo

27. When to Use Recursion?When to Use Recursion?
 Avoid recursion when an obvious iterativeAvoid recursion when an obvious iterative
algorithm existsalgorithm exists
Examples: factorial, Fibonacci numbersExamples: factorial, Fibonacci numbers
 Use recursion for combinatorial algorithmUse recursion for combinatorial algorithm
where at each step you need to recursivelywhere at each step you need to recursively
explore more than one possible continuationexplore more than one possible continuation
Examples: permutations, all paths in labyrinthExamples: permutations, all paths in labyrinth
If you have only one recursive call in the body ofIf you have only one recursive call in the body of
a recursive method, it can directly becomea recursive method, it can directly become
iterative (like calculating factorial)iterative (like calculating factorial)
27

28. SummarySummary
 Recursion means to call a method from itselfRecursion means to call a method from itself
It should always have a bottom at whichIt should always have a bottom at which
recursive calls stoprecursive calls stop
 Very powerful technique for implementingVery powerful technique for implementing
combinatorial algorithmscombinatorial algorithms
Examples: generating combinatorialExamples: generating combinatorial
configurations like permutations,configurations like permutations,
combinations, variations, etc.combinations, variations, etc.
 Recursion can be harmful when not usedRecursion can be harmful when not used
correctlycorrectly
28

29. Questions?Questions?
RecursionRecursion
http://academy.telerik.com

30. ExercisesExercises
1.1. Write a recursive program that simulates executionWrite a recursive program that simulates execution
of n nested loops from 1 to n. Examples:of n nested loops from 1 to n. Examples:
1 1 11 1 1
1 1 21 1 2
1 1 31 1 3
1 1 1 2 11 1 1 2 1
n=2 -> 1 2 n=3 -> ...n=2 -> 1 2 n=3 -> ...
2 1 3 2 32 1 3 2 3
2 2 3 3 12 2 3 3 1
3 3 23 3 2
3 3 33 3 3
30

31. Exercises (2)Exercises (2)
2.2. Write a recursive program for generating andWrite a recursive program for generating and
printing all the combinations with duplicates of kprinting all the combinations with duplicates of k
elements from n-element set. Example:elements from n-element set. Example:
n=3, k=2n=3, k=2  (1 1), (1 2), (1 3), (2 2), (2 3), (3 3)(1 1), (1 2), (1 3), (2 2), (2 3), (3 3)
3.3. Write a recursive program for generating andWrite a recursive program for generating and
printing all permutations of the numbers 1, 2, ..., nprinting all permutations of the numbers 1, 2, ..., n
for given integer number n. Example:for given integer number n. Example:
n=3n=3  {1, 2, 3}, {1, 3, 2}, {2, 1, 3},{1, 2, 3}, {1, 3, 2}, {2, 1, 3},
{2, 3, 1}, {3, 1, 2},{3, 2, 1}{2, 3, 1}, {3, 1, 2},{3, 2, 1}
31

32. Exercises (3)Exercises (3)
4.4. Write a recursive program for generating andWrite a recursive program for generating and
printing all ordered k-element subsets from n-printing all ordered k-element subsets from n-
element setelement set (variations V(variations Vkk
nn).).
Example: n=3, k=2Example: n=3, k=2
(1 1), (1 2), (1 3), (2 1), (2 2), (2 3), (3 1), (3 2), (3 3)(1 1), (1 2), (1 3), (2 1), (2 2), (2 3), (3 1), (3 2), (3 3)
4.4. Write a program for generating and printingWrite a program for generating and printing allall
subsetssubsets ofof k strings fromk strings from given set of strings.given set of strings.
Example: s = {test,Example: s = {test, rockrock,, funfun}}, k=2, k=2
(test(test rockrock)),, (test(test funfun)),, ((rockrock funfun))
32

33. Exercises (4)Exercises (4)
6.6. We are given a matrix of passable and non-passableWe are given a matrix of passable and non-passable
cells. Write a recursive program for finding all pathscells. Write a recursive program for finding all paths
between two cells in the matrix.between two cells in the matrix.
7.7. Modify the above program to check whether a pathModify the above program to check whether a path
exists between two cells without finding all possibleexists between two cells without finding all possible
paths. Test it over an empty 100 x 100 matrix.paths. Test it over an empty 100 x 100 matrix.
8.8. Write a program to find the largest connected areaWrite a program to find the largest connected area
of adjacent empty cells in a matrix.of adjacent empty cells in a matrix.
9.9. Implement the BFS algorithm to find the shortestImplement the BFS algorithm to find the shortest
path between two cells in a matrix (read aboutpath between two cells in a matrix (read about
Breath-First SearchBreath-First Search in Wikipedia).in Wikipedia).
33

34. Exercises (5)Exercises (5)
6.6. We are given a matrix of passable and non-passableWe are given a matrix of passable and non-passable
cells. Write a recursive program for finding all areascells. Write a recursive program for finding all areas
of passable cells in the matrix.of passable cells in the matrix.
10.10. Write a recursive program that traverses the entireWrite a recursive program that traverses the entire
hard disk drive C: and displays all folders recursivelyhard disk drive C: and displays all folders recursively
and all files inside each of them.and all files inside each of them.
34