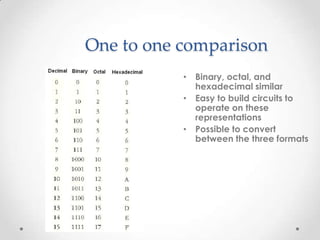
This document discusses data representation and number systems in computers. It covers binary, octal, decimal, and hexadecimal number systems. Key points include: - Data in computers is represented using binary numbers and different number systems allow for more efficient representations. - Converting between number systems like binary, octal, decimal, and hexadecimal is explained through examples of dividing numbers and grouping bits. - Signed numbers can be represented using complement representations like one's complement and two's complement, with subtraction implemented through addition of complements. Fast methods for calculating two's complement are described.

1. Chapter 2
Data Representation
• Data Representation
• Compliments
• Subtraction of Unsigned Numbers
using r’s complement
• How To Represent Signed Numbers
• Floating-Point Representation

2. Data Types
• The data types stored in digital computers
may be classified as being one of the
following categories:
1. numbers used in arithmetic computations,
2. letters of the alphabet used in data
processing, and
3. other discrete symbols used for specific
purposes.
All types of data are represented in computers in
binary-coded form.

3. Binary Numbers
• Binary numbers are made of binary digits (bits):
0 and 1
• Convert the following to decimal
(1011)2 = 1x23 + 0x22 + 1x21 + 1x20 = (11)10

4. Example
• Use radix representation to convert the binary number
(101.01) into decimal.
• The position value is power of 2
• 1 0 1. 0 1
•
• 22 21 20 2-1 2-2
• 4 + 0 + 1 + 0 + 1/22 = 5.25
(101.01)2  (5.25)10

5. Converting an Integer from Decimal to Another
Base
• Divide the decimal number by the base (e.g.
• The remainder is the lowest-order digit
• Repeat the first two steps until no divisor
remains.
• For binary the even number has no remainder
‘0’, while the odd has ‘1’
For each digit position:

6. Converting an Integer from Decimal to
Another Base
Example
for (13)10:
Integer
Quotient
13/2 = (12+1)½ a0 = 1
6/2 = ( 6+0 )½ a1 = 0
3/2 = (2+1 )½ a2 = 1
1/2 = (0+1) ½ a3 = 1
Remainder Coefficient
Answer (13)10 = (a3 a2 a1 a0)2 = (1101)2

7. Converting a Fraction from Decimal
to Another Base
Example for
(0.625)10: Integer
0.625 x 2 = 1 + 0.25 a-1 = 1
0.250 x 2 = 0 + 0.50 a-2 = 0
0.500 x 2 = 1 + 0 a-3 = 1
Fraction Coefficient
Answer (0.625)10 = (0.a-1 a-2 a-3 )2 = (0.101)2

8. DECIMAL TO BINARY CONVERSION
(INTEGER+FRACTION)
(1) Separate the decimal number into integer and fraction parts.
(2) Repeatedly divide the integer part by 2 to give a quotient
and a remainder and
Remove the remainder. Arrange the sequence of remainders
right to left from the period. (Least significant bit first)
(3) Repeatedly multiply the fraction part by 2 to give an integer
and a fraction part
and remove the integer. Arrange the sequence of integers
left to right from the period. (Most significant fraction bit first)

9. (Example) (41.6875)10 (?)2
Integer = 41, Fraction = 0.6875
The first procedure produces
41= 1 x 25 + 0 x 24 + 1 x 23 + 0 x 22 + 0 x 2 + 1 = (101001)
0.6875=0.1011
41.6875 (10) = 101001.1011 (2)
Integer remainder
41 /2 1
20 0
10 0
5 1
2 0
1 1
Overflow Fraction
X by 2 .6875
1 .3750
0 .750
1 .5
1 0

10. Octal Numbers
• Octal numbers (Radix or base=8) are made of octal
digits: (0,1,2,3,4,5,6,7)
• How many items does an octal number represent?
• Convert the following octal number to decimal
(465.27)8 = 4x82 + 6x81 + 5x80 + 2x8-1 + 7x8-2

11. Converting an Integer from Decimal
to Octal
Example for (0.3125)10:
Integer
0.3125 x 8 = 2 + 0.5 a-1 = 2
0.5000 x 8 = 4 + 0 a-2 = 4
Fraction Coefficient
Answer (0.3125)10 = (0.24)8
Combine the two (175.3125)10 = (257.24)8
Remainder
of division
Overflow of
multiplication

12. Hexadecimal Numbers
• Hexadecimal numbers are made of 16 symbols:
o (0,1,2,3,4,5,6,7,8,9,A, B, C, D, E, F)
• Convert a hexadecimal number to decimal
o (3A9F)16 = 3x163 + 10x162 + 9x161 + 15x160 = 1499910
• Hexadecimal with fractions:
o (2D3.5)16 = 2x162 + 13x161 + 3x160 + 5x16-1 = 723.312510
• Note that each hexadecimal digit can be
represented with four bits.
o (1110) 2 = (E)16
• Groups of four bits are called a nibble.
o (1110) 2

13. Example
• Convert the decimal number
(107.00390625)10 into hexadecimal number.
• (107.00390625)10  (6B.01)16
Integer remainde
r
107 Divide/16
6 11=B
0 6
Overflow Fraction
X by 16 .
00390625
0 .0625
1 .0000
.
Closer to
the period

14. Conversion Between Number Bases
Decimal(base 10)
Octal(base 8)
Binary(base 2)
Hexadecimal
(base16)
° We normally convert to base 10
because we are naturally used to the
decimal number system.
° We can also convert to other number
systems

15. One to one comparison
• Binary, octal, and
hexadecimal similar
• Easy to build circuits to
operate on these
representations
• Possible to convert
between the three formats

16. Converting between Base 16 and
Base 2
° Conversion is easy!
 Determine 4-bit value for each hex digit
° Note that there are 24 = 16 different values of
four bits which means each 16 value is
converted to four binary bits.
° Easier to read and write in hexadecimal.
° Representations are equivalent!
3A9F16 = 0011 1010 1001 11112
3 A 9 F

17. Converting between Base 16 and
Base 8
1. Convert from Base 16 to Base 2
2. Regroup bits into groups of three starting from right
3. Ignore leading zeros
4. Each group of three bits forms an octal digit (8 is
represented by 3 binary bits).
352378 = 011 101 010 011 1112
5 2 3 73
3A9F16 = 0011 1010 1001 11112
3 A 9 F

18. Example
Convert 101011110110011 to
a. octal number
b. hexadecimal number
a. Each 3 bits are converted to octal :
(101) (011) (110) (110) (011)
5 3 6 6 3
101011110110011 = (53663)8
b. Each 4 bits are converted to hexadecimal:
(0101) (0111) (1011) (0011)
5 7 B 3
101011110110011 = (57B3)16
Conversion from binary to hexadecimal is similar except that the bits
divided into groups of four.

19. Compliments
Complements Of Numbers

20. Subtraction using
addition
• Conventional addition (using carry) is easily
• implemented in digital computers.
• However; subtraction by borrowing is
difficult and inefficient for digital computers.
• Much more efficient to implement
subtraction using ADDITION OF the
COMPLEMENTS of numbers.

21. Binary Addition
1 1 1 1 0 1
+ 1 0 1 1 1
---------------------
0
1
0
1
1
1111
1 1 00
carries
Example Add (11110)2 to
(10111)2
(111101)2 + (10111) 2 = (1010100)2
carry

22. Binary Subtraction
• We can also perform subtraction (with borrows).
• Example: subtract (10111) from (1001101)
1 10
0 10 10 0 0 10
1 0 0 1 1 0 1
- 1 0 1 1 1
------------------------
0 1 1 0 1 1 0
borrows
1+1=
2
(1001101)2 - (10111)2 = (0110110)2

23. The complement 1’s of
1011001 is 0100110
0 1 1 0 0- 1
1 1 1 1 1 1
1 0 0 1 1 0
0 0 1 1 1- 1
1 1 1 1 1 1
1 1 0 0 0 0
1
1
0
The 1’s complement of
0001111 is 1110000
0
1
1
l’s complement

24. For binary numbers, r = 2,
r’s complement is the 2’s complement.
The 2’s complement of N is 2n - N.
2’s complement
Digit
n
Digit
n-1
Next
digit
Next
digit
First
digit
0 0 0 0 0
-
1

25. 2’s complement Example
The 2’s complement of
1011001 is 0100111
The 2’s complement of
0001111 is 1110001
0 1 1 0 0- 1
0 0 0 0 0 0
1 0 0 1 1 1
0 0 1 1 1- 1
1 1 0 0 0 1
1
0
0
0
1
1
0 0 0 0 0 001

26. Fast Methods for 2’s
Complement
Method 1:
The 2’s complement of binary number is obtained by adding 1 to the
l’s complement value.
Example:
1’s complement of 101100 is 010011 (invert the 0’s and 1’s)
2’s complement of 101100 is 010011 + 1 = 010100

27. Fast Methods for 2’s
Complement
Method 2:
The 2’s complement can be formed by leaving all least significant 0’s
and the first 1 unchanged, and then replacing l’s by 0’s and 0’s by l’s
in all other higher significant bits.
Example:
The 2’s complement of 1101100 is
0010100
Leave the two low-order 0’s and the first 1 unchanged, and then
replacing 1’s by 0’s and 0’s by 1’s in the four most significant bits.

28. Examples
o Finding the 2’s complement of (01100101)2
• Method 1 – Simply complement each bit and
then add 1 to the result.
(01100101)2
[N] = 2’s complement = 1’s complement (10011010)2
+1
=(10011011)2
• Method 2 – Starting with the least significant
bit, copy all the bits up to and including the
first 1 bit and then complement the remaining
bits.
N = 0 1 1 0 0 1 0 1
[N] = 1 0 0 1 1 0 1 1

29. Video Reference
• http://www.youtube.com/watch?v=SXAr35BiqK8