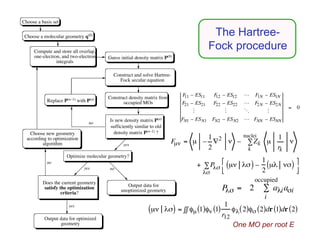
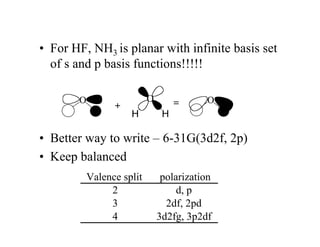
The document discusses basis sets and linear combination of atomic orbitals (LCAO) wave functions used in Hartree-Fock theory. It explains that atomic orbitals like Slater-type orbitals are approximated using Gaussian functions for calculations. Basis sets like STO-3G use a minimal number of primitive Gaussians to represent atomic orbitals, while more advanced basis sets like 6-31G add polarization and diffuse functions for improved accuracy.

1. Ab
Ini'o
Hartree-­‐Fock
Theory
Basis
Sets
and
LCAO
Wave
Func'ons
Video
IV.i

2. A One-Slide Summary of Quantum Mechanics
Fundamental Postulate:
O ! = a !
operator
wave function
(scalar)
observable
What is !? ! is an oracle!
Where does ! come from? ! is refined
Variational Process
H! = E !
Energy (cannot go
lower than "true" energy)
Hamiltonian operator
(systematically improvable)
electronic road map: systematically
improvable by going to higher resolution convergence of E
truth
What if I can't converge E ? Test your oracle with a question to which you
already know the right answer...

3. Constructing a 1-Electron Wave Function
The units of the wave function are such that its square is electron per
volume. As electrons are quantum particles with non-point distributions,
sometimes we say “density” or “probability density” instead of electron per
volume (especially when there is more than one electron, since they are
indistinguishable as quantum particles)
For instance, a valid wave function in cartesian coordinates for one electron
might be:
" x,y,z;Z
( ) =
2Z5/2
81 #
6 $ Z x2
+ y2
+ z2
%
&
'
(
)
*ye
$Z x2
+y2
+z2
/ 3
normalization
factor
radial phase
factor
cartesian
directionality
(if any)
ensures
square
integrability

4. Constructing a 1-Electron Wave Function
To permit additional flexibility, we may take our wave function to be a linear
combination of some set of common “basis” functions, e.g., atomic orbitals
(LCAO). Thus
!
" r
( ) = ai# r
( )
i=1
N
$
For example, consider the wave
function for an electron in a C–H bond.
It could be represented by s and p
functions on the atomic positions, or s
functions along the bond axis, or any
other fashion convenient. H
C

5. Constructing a 1-Electron Wave Function
To optimize the coefficients in our LCAO expansion, we use the variational
principle, which says that
!
E =
ai"i
i
#
$
%
&
&
'
(
)
)
* H a j" j
j
#
$
%
&
&
'
(
)
)
dr
ai"i
i
#
$
%
&
&
'
(
)
)
* a j" j
j
#
$
%
&
&
'
(
)
)
dr
=
aia j
ij
# "i
* H" j dr
aia j
ij
# "i
* " j dr
=
aia j
ij
# ij
H
aia j
ij
# ij
S
which is minimized by one root E of the “secular equation” (the
other roots are excited states)—each value of E that satisfies the
secular equation determines all of the ai values and thus the shape
of the molecular orbital wave function (MO)
H11 – ES11 H12 – ES12 L H1N – ES1N
H21 – ES21 H22 – ES22 L H2N – ES2 N
M M O M
HN1 – ESN1 HN2 – ESN2 L HNN – ESNN
= 0

6. What Are These Integrals H?
The electronic Hamiltonian includes kinetic energy, nuclear attraction, and,
if there is more than one electron, electron-electron repulsion
The final term is problematic. Solving for all electrons at once is a
many-body problem that has not been solved even for classical
particles. An approximation is to ignore the correlated motion of the
electrons, and treat each electron as independent, but even then, if
each MO depends on all of the other MOs, how can we determine
even one of them? The Hartree-Fock approach accomplishes this
for a many-electron wave function expressed as an
antisymmetrized product of one-electron MOs (a so-called Slater
determinant)
!
Hij = "i #
1
2
$2
" j # "i
Zk
rk
k
nuclei
% " j + "i
&
2
rn
n
electrons
% " j

7. Choose a basis set
Choose a molecular geometry q(0)
Compute and store all overlap,
one-electron, and two-electron
integrals
Guess initial density matrix P(0)
Construct and solve Hartree-
Fock secular equation
Construct density matrix from
occupied MOs
Is new density matrix P(n)
sufficiently similar to old
density matrix P(n–1) ?
Optimize molecular geometry?
Does the current geometry
satisfy the optimization
criteria?
Output data for optimized
geometry
Output data for
unoptimized geometry
yes
Replace P(n–1) with P(n)
no
yes no
Choose new geometry
according to optimization
algorithm
no
yes
Fµ! = µ –
1
2
"2 ! – Zk
k
nuclei
# µ
1
rk
!
+ P$%
$%
# µ! $%
( ) –
1
2
µ$ !%
( )
&
'
(
)
µ! "#
( ) = $µ
%% 1
( )$! 1
( )
1
r12
$" 2
( )$# 2
( )dr 1
( )dr 2
( )
P!" = 2 a!i
i
occupied
# a"i
The Hartree-
Fock procedure
F
11 – ES11 F
12 – ES12 L F1N – ES1N
F21 – ES21 F22 – ES22 L F2N – ES2N
M M O M
FN1 – ESN1 FN2 – ESN2 L FNN – ESNN
= 0
One MO per root E

8. • Slater Type Orbitals (STO)
– Can’t do 2 electron integrals analytically
!
1s
" =
#
$
%
&
'
(
)
*
1
2
e#+r
( ) ( ) ( ) ( ) 2
1
12
2
2
1
1
1 dr
dr
r
!
"
#
µ $
$
$
$
%%
What functions to use?

9. • 1950s
– Replace with something similar that is
analytical: a gaussian function
!
1s
" =
#
$
%
&
'
(
)
*
1
2
e# +r
!
"1s"
" =
2#
$
%
&
'
(
)
*
3
4
e+#r2
VS.

10. Approximating Slater Functions with Gaussians
!
" r
( ) = ai# r
( )
i=1
N
$
primitive gaussians
STO-3G
Slater function
Contracted basis function

11. "1s"
" = ai
i
N
#
2$i
%
&
'
(
)
*
+
3
4
e,$i
r2
Contracted Basis Set
• STO-#G - minimal basis
• Pople - optimized a and α values

12. • What do you about very different bonding
situations?
– Have more than one 1s orbital
• Multiple-ζ(zeta) basis set
– Multiple functions for the same atomic orbital
H F vs. H H

13. • Double-ζ – one loose, one tight
– Adds flexibility
• Triple-ζ – one loose, one medium, one tight
• Only for valence

14. • Decontraction
– Allow ai to vary
• Pople - #-##G
– 3-21G
!
"1sH
STO#3G
= ai
i
3
$
2%i
&
'
(
)
*
+
,
3
4
e#%i
r2
locked in STO-3G
primitive gaussians
primitives in all core functions
valence: 2 tight, 1 loose
gaussian

15. How many basis functions are for NH3 using 3-21G?
NH3 3-21G
atom # atoms AO degeneracy basis fxns primitives total basis fxns total primitives
N 1 1s(core) 1 1 3 1 3
2s(val) 1 2 2 + 1 = 3 2 3
2p(val) 3 2 2 + 1 = 3 6 9
H 3 1s(val) 1 2 2 + 1 = 3 6 9
total = 15 24

16. Polarization Functions
• 6-31G**
6 primitives
1 core basis functions
2 valence basis functions
one with 3 primitives, the other with 1
1 d functions on all heavy atoms (6-fold deg.)
1 p functions on all H (3-fold deg.)

17. • For HF, NH3 is planar with infinite basis set
of s and p basis functions!!!!!
• Better way to write – 6-31G(3d2f, 2p)
• Keep balanced
Valence split polarization
2 d, p
3 2df, 2pd
4 3d2fg, 3p2df
O
+
O
H H
= O

18. Dunning basis set
cc-pVNZ
correlation consistent
polarized
N = D, T, Q, 5, 6

19. Diffuse functions
• “loose” electrons
– anions
– excited states
– Rydberg states
• Dunning - aug-cc-pVNZ
– Augmented
• Pople
– 6-31+G - heavy atoms/only with valence
– 6-31++G - hydrogens
• Not too useful

20. How many basis functions in H2POH
using 6-31G(d, p)?