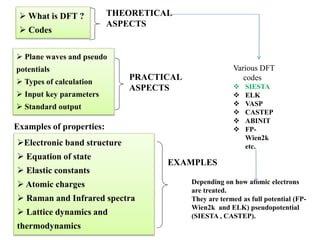
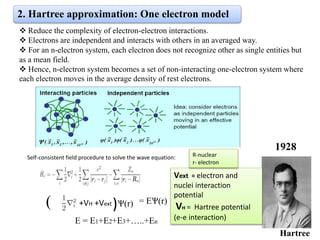
The document discusses Density Functional Theory (DFT) and its foundational concepts, including the Schrödinger equation, the Born-Oppenheimer approximation, and various methods for addressing many-body problems in quantum mechanics. It highlights the development of DFT as a means to simplify complex calculations by focusing on electron density instead of wave functions, while detailing various computational codes like VASP and SIESTA. Key historical contributions from scientists such as Hohenberg, Kohn, and Sham are emphasized, alongside the introduction of approximation techniques like the Local Density Approximation (LDA) and Generalized Gradient Approximation (GGA).

1. Schrödinger
Max Born and Robert
Oppenheimer Hartee and Fock

2. Electronic band structure
 Equation of state
 Elastic constants
 Atomic charges
 Raman and Infrared spectra
 Lattice dynamics and
thermodynamics
THEORETICAL
ASPECTS
PRACTICAL
ASPECTS
EXAMPLES
Various DFT
codes
 SIESTA
 ELK
 VASP
 CASTEP
 ABINIT
 FP-
Wien2k
etc.
Depending on how atomic electrons
are treated.
They are termed as full potential (FP-
Wien2k and ELK) pseudopotential
(SIESTA , CASTEP).
 What is DFT ?
 Codes
 Plane waves and pseudo
potentials
 Types of calculation
 Input key parameters
 Standard output
Examples of properties:

3. Why Density Functional Theory ?
 The calculation of physical and chemical properties of multi- particle systems (atoms,
molecules or solids) require the
exact determination of electronic structure and total energy of these systems.
 Schrödinger equation successfully explains the electronic structure of simple systems
and numerically exact solutions
are found for small no. of atoms and molecules.
 This n-electron problem was solved when Kohn and Sham in 1965 formulated a theory
concerning 3-dimensional
electron density and energy functionals.
Electron density n(r) plays central role instead of wave function ψ(r). The problem
of many-interacting particles system in static potential is reduced to non-interacting
single particle system in an effective potential.

4. Many body problem:
 For large interacting system, we first need to consider a many particle wave
function.
 Many body Hamiltonian for electron and nucleus is of the form given below
Hѱ (r,R,t) =E ѱ (r,R,t)
Innocent look of wave equation
1926
Hѱ
=
M
m
e
Schrödinger
Hѱ
=
=
Ѱ
=
ѱ
=
ѱ

5. 1. Born-Oppenheimer approximation:
Since the total hamiltonian for electron and nucleus is:
then the hamiltonian for the electronic part
will be
1927
Approximations for solving many body problem
 The Born-Oppenheimer approximation
 Hartree approximation
 Hartree-Fock method
 Hohenberge- Kohen
 Kohn-Sham approach (Walter Kohn and Lu.J.Sham)
Max Born and Robert
Oppenheimer
 The nuclei are much heavier than electrons.
 They move much more slowly and hence neglect the nuclear
kinetic energy.
 The wave function separated into electronic and nuclear part
and determine motion of electrons with nuclei held fixed.
Hѱ =
=
Hѱ
=

6. 2. Hartree approximation: One electron model
1928
 Reduce the complexity of electron-electron interactions.
 Electrons are independent and interacts with others in an averaged way.
 For an n-electron system, each electron does not recognize other as single entities but
as a mean field.
 Hence, n-electron system becomes a set of non-interacting one-electron system where
each electron moves in the average density of rest electrons.
Hartree
Self-consistent field procedure to solve the wave equation:
Vext = electron and
nuclei interaction
potential
VH = Hartree potential
(e-e interaction)
( )
+VH +Vext Ѱ(r) = EѰ(r)
E = E1+E2+E3+…..+En
R-nuclear
r- electron

7. Hartree method produced crude estimation of energy due to two
oversimplifications:
 Hartree method does not follow two basic principles of quantum
mechanics: the antisymmetry principle and Pauli’s exclusion principle.
 Does not count the exchange and correlation energies coming from n-
electron nature.
The Hartree method, therefore, was soon refined into the Hartree-Fock method…...continue…
Hartree
3. Hartree-Fock method
Based on the one-electron and mean-field approach by Hartree, V.A. Fock enhanced the
methods to higher perfection. Fock and J.C. Slater in 1930 generalised the Hartree's theory to
take into account the antisymmetry requirement.
 In HF method, the n-electron wave function approximated as a linear
combination of non-interacting one-electron wave function in the form of
Slater determinant.
Slater
determinant
Fock
1930

8. VH = Vij Hartree or Coulomb interaction
energy of two electrons
Ex = Exchange energy comes from the
antisymmetric nature of wave function in
the Slater determinant.
Difficulties with Hartree-Fock Theory:
A new approach has been developed known as Density Functional Theory (DFT).
 In 1964 Hohenberg and Kohn showed that schrodinger equation (3N dimensional e.g. 10
electrons require 30 dimensions) could be reformulated in terms of electron density n(r)
with non-interacting n separate 3-dimensional ones.
 The main objective of DFT is to replace the many-particle electronic wavefunction with
the electron density as the basic quantity.
 The electron density n(r), the central player in DFT decides everything in an n-electron
quantum state where there is no individual electron density but a 3-dimensional density of
electrons.
 The addition of all the electron densities over the whole space naturally return to the total
number of electrons in the system.
 The knowledge of overlapping of atomic electron density, roughly generate the electron
density of the solids.
 This theory gives approximate solutions to both Exchange and Correlation Energies.
 Correlation energy and
 Problem of dealing 3N dimensional .
)ѱ(r) = E ѱ(r)
E = Ekin+ EH +Eext + Ex

9. The Fundamental Pillars of DFT
First Hohenberg Kohn (HK) theorem: The ground-state energy
is a unique functional of the electron density n(r).
 This theorem provides one to one mapping between ground
state wave function and ground state charge density.
 The ground state charge density can uniquely describe all
the ground state properties of system.
 The fundamental concept behind density functional theory
is that charge density (3-Dimensional) can correctly describe
the ground state of N-particle instead of using a wave
function (3N-Dimensional).
Second Hohenberg Kohn (HK) theorem: The electron density that minimizes the
energy of the overall functional is the true electron density.
 If the true functional form of energy in terms of density gets known, then
one could vary the electron density until the energy from the functional is
minimized, giving us required ground state density.
 This is essentially a variational principle and is used in practice with
approximate forms of the functional.
 The simplest possible choice of a functional can be a constant electron
density all over the space.

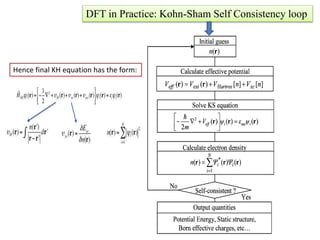
10. 5. Kohn- Sham Approach (1965):
 KS replace the interacting n-electron system with a system of one-electron (non-
interacting) system in effective potential having the same ground state.
since the kinetic energy; E= Ekin+ Eext+EH +Ex+ Ec
int
non
non int
Ekin = Ekin + Ekin
where
E = Ekin + Ekin + Eext + EH +Ex + Ec
int
non int
E = Ekin + Eext + EH +Exc = F [n(r)] + Eext
non

11. Hence final KH equation has the form:
DFT in Practice: Kohn-Sham Self Consistency loop

12. DFT in Practice: The exchange-
correlation Functional
1. Local density approximation (LDA)
Exchange-correlation approximation
 Approximation used to find out exchange-
correlation function.
 Exchange-correlation energy functional is
purely local.
 Ignores corrections to the exchange-
correlation energy at a point r due to nearby
inhomogeneities in the electron density.
2. Generalized Gradient Approximation (GGA)
 Depends on local density and its gradient.
 GGA uses information about the local electron density and
also the local gradient in the electron density.
Though GGA includes more physical information than LDA
It is not necessary that it must be more accurate.
There are large number of distinct GGA functionals depending
on the ways in which information from the gradient of the
electron density can be included in a GGA functional.

13. In Summary