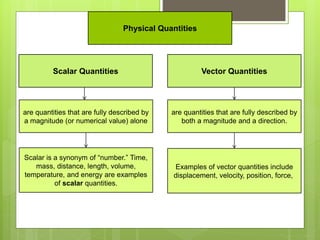
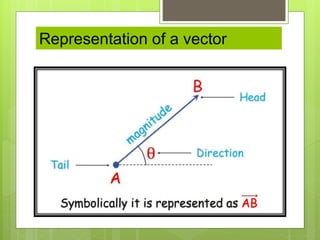
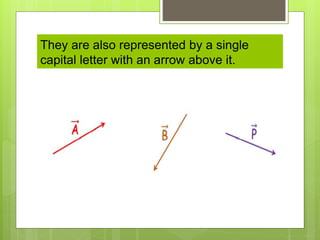
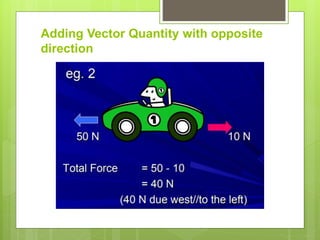
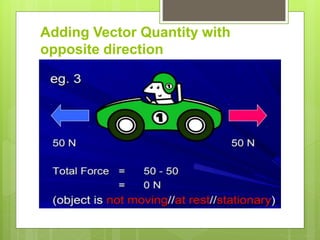
This document defines scalar and vector quantities in physics. Scalars have only magnitude, while vectors have both magnitude and direction. Examples of scalars include time, mass, and temperature, while vectors include displacement, velocity, and force. Vectors are represented by arrows. Scalar quantities can be simply added or subtracted, while adding vectors requires considering both magnitude and direction, such as combining velocities in the same or opposite directions.

1. Basics in Physics
Basics of Scalar and
Vector Quantity
Prepared by:
Cynthia D. Sanico

2. Learning Outcomes
 Define scalar and vector quantities
 Give examples of scalar and vector quantities
 Solve problems related to scalar and vector
quantities

3.  Physics is a mathematical science. The underlying
concepts and principles have a mathematical basis.
Throughout the course of our study of physics, we
will encounter a variety of concepts that have a
mathematical basis associated with them. While our
emphasis will often be upon the conceptual nature of
physics, we will give considerable and persistent
attention to its mathematical aspect.

4.  The motion of objects can be described by words. Even a person
without a background in physics has a collection of words that can
be used to describe moving objects. Words and phrases such
as going fast, stopped, slowing down, speeding up,
and turning provide a sufficient vocabulary for describing the
motion of objects.
 In physics, we use these words and many more. We will be
expanding upon this vocabulary list with words such
as distance, displacement, speed, velocity, and acceleration. As we
will soon see, these words are associated with mathematical
quantities that have strict definitions. The mathematical quantities
that are used to describe the motion of objects can be divided into
two categories. The quantity is either a vector or a scalar. These two
categories can be distinguished from one another by their distinct
definitions:

5. Physical Quantities
Scalar Quantities Vector Quantities
are quantities that are fully described by
a magnitude (or numerical value) alone
are quantities that are fully described by
both a magnitude and a direction.
Scalar is a synonym of “number.” Time,
mass, distance, length, volume,
temperature, and energy are examples
of scalar quantities.
Examples of vector quantities include
displacement, velocity, position, force,

6. Example of scalar quantity

7. Example of scalar quantity

8. Example of scalar quantity

9. Example of scalar quantity

10. Example of vector quantity

11. Example of vector quantity

12. Representation of a vector

13. They are also represented by a single
capital letter with an arrow above it.

14. Some vector quantities are
represented by their respective
symbols with an arrow above it.

15. Adding Scalar Quantity
 Can be added, subtracted, multiplied and divided like
ordinary numbers.
Sample problem:
(a) 3 kg of sand is added to 1 kg cement, resulting mixture has a
mass of 4 kg
(b) 5 liters of water are poured from a pail that has 8 liters of
water in it. What is the resulting volume of water?
Ans. 3 L
No direction is involved!

16. Scalar Quantities

17. Adding Vector Quantity
 An arrow is used to represent the magnitude and
direction of a vector quantity.
 Example
velocity of airplane = 100 km/h
wind velocity = 20 km/h
 (a) If same direction, Resulting velocity of
airplane= 100 + 20 = 120 km/h
 (a) If opposite direction, resulting velocity of
airplane = 100 -20 = 80 km/h

18. Adding Vector Quantity with same
direction

19. Adding Vector Quantity with opposite
direction

20. Adding Vector Quantity with
opposite direction

21.  A resultant force is the force (magnitude and
direction) obtained when two or more forces
are combined

22. Derivation of formula
 F=N (SI unit)
 F=m(vf-vi/t)
 F=m(m/s-m/s/t)
 F=m(m/s/t)
 F=m(m/s2)
 F= kg⦁m/s2 (SI base units)
 F=ma
 F=N(SI unit)
a=m/s2