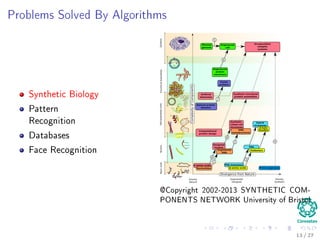
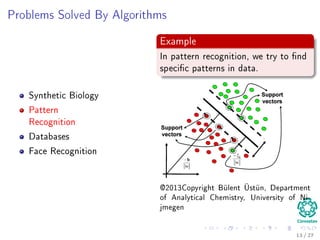
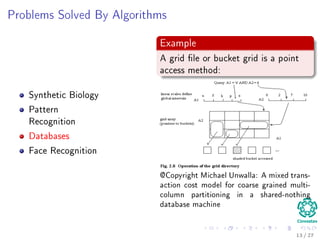
The document provides an introduction to algorithms, detailing their definitions, the problems they can solve, and their analysis methods. It outlines a syllabus for a course that covers various topics in algorithm analysis, including growth functions, sorting techniques, and advanced data structures. Additionally, it emphasizes the importance of analyzing algorithms in terms of time complexity and problem-solving efficiency.




















![An Example of an Algorithm
Insertion Sort Algorithm
Data: Unsorted Sequence A
Result: Sort Sequence A
Insertion Sort(A)
for j ← 2 to lenght(A) do
key ← A[j];
// Insert A[j] into the sorted sequence A[1, ..., j − 1]
i ← j − 1;
while i > 0 and A[i] > key do
A[i + 1] ← A[i];
i ← i − 1;
end
A[i + 1] ← key
end
13 / 36](https://image.slidesharecdn.com/01introductionslideshare-150316145938-conversion-gate01/85/01-Analysis-of-Algorithms-Introduction-24-320.jpg)


























![Please follow these simple rules
Insertion Sort(A)
1 for j ← 2 to length(A)
2 do
3 key ← A[j]
4 Insert A[j] into the sorted sequence A[1, ..., j − 1]}
5 i ← j − 1
6 while i > 0 and A[i] > key
7 do
8 A[i + 1] ← A[i]
9 i ← i − 1
10 A[i + 1] ← key
Rule
Always put the name of the algorithm at the top.
Together with the input.
22 / 36](https://image.slidesharecdn.com/01introductionslideshare-150316145938-conversion-gate01/85/01-Analysis-of-Algorithms-Introduction-52-320.jpg)
![Please follow these simple rules
Insertion Sort(A)
1 for j ← 2 to length(A)
2 do
3 key ← A[j]
4 Insert A[j] into the sorted sequence A[1, ..., j − 1]}
5 i ← j − 1
6 while i > 0 and A[i] > key
7 do
8 A[i + 1] ← A[i]
9 i ← i − 1
10 A[i + 1] ← key
Rule
Always initialize all the variables.
The a ← b means that the value b is passed to a. You also can use
"=."
22 / 36](https://image.slidesharecdn.com/01introductionslideshare-150316145938-conversion-gate01/85/01-Analysis-of-Algorithms-Introduction-53-320.jpg)
![Please follow these simple rules
Insertion Sort(A)
1 for j ← 2 to length(A)
2 do
3 key ← A[j]
4 Insert A[j] into the sorted sequence A[1, ..., j − 1]}
5 i ← j − 1
6 while i > 0 and A[i] > key
7 do
8 A[i + 1] ← A[i]
9 i ← i − 1
10 A[i + 1] ← key
Rule
Use identation to preserve the block structure avoiding clutter
22 / 36](https://image.slidesharecdn.com/01introductionslideshare-150316145938-conversion-gate01/85/01-Analysis-of-Algorithms-Introduction-54-320.jpg)
![Please follow these simple rules
Insertion Sort(A)
1 for j ← 2 to length(A)
2 do
3 key ← A[j]
4 Insert A[j] into the sorted sequence A[1, ..., j − 1]}
5 i ← j − 1
6 while i > 0 and A[i] > key
7 do
8 A[i + 1] ← A[i]
9 i ← i − 1
10 A[i + 1] ← key
Rule
It corresponds to comments. You can also use "//"
22 / 36](https://image.slidesharecdn.com/01introductionslideshare-150316145938-conversion-gate01/85/01-Analysis-of-Algorithms-Introduction-55-320.jpg)














![Counting the Operations
Insertion Sort(A) length(A):=N
1 for j← 2 to length(A)
2 do
3 key ← A[j]
4 Insert A[j] into the sorted sequence A[1, ..., j − 1]}
5 i ← j − 1
6 while i > 0 and A[i] > key
7 do
8 A[i + 1] ← A[i]
9 i ← i − 1
10 A[i + 1] ← key
Count Value
c1N
31 / 36](https://image.slidesharecdn.com/01introductionslideshare-150316145938-conversion-gate01/85/01-Analysis-of-Algorithms-Introduction-71-320.jpg)
![Counting the Operations
Insertion Sort(A) length(A):=N
1 for j← 2 to length(A)
2 do
3 key ← A[j]
4 Insert A[j] into the sorted sequence A[1, ..., j − 1]}
5 i ← j − 1
6 while i > 0 and A[i] > key
7 do
8 A[i + 1] ← A[i]
9 i ← i − 1
10 A[i + 1] ← key
Count Value
c2(N − 1)
31 / 36](https://image.slidesharecdn.com/01introductionslideshare-150316145938-conversion-gate01/85/01-Analysis-of-Algorithms-Introduction-72-320.jpg)
![Counting the Operations
Insertion Sort(A) length(A):=N
1 for j← 2 to length(A)
2 do
3 key ← A[j]
4 Insert A[j] into the sorted sequence A[1, ..., j − 1]}
5 i ← j − 1
6 while i > 0 and A[i] > key
7 do
8 A[i + 1] ← A[i]
9 i ← i − 1
10 A[i + 1] ← key
Count Value
c3(N − 1)
31 / 36](https://image.slidesharecdn.com/01introductionslideshare-150316145938-conversion-gate01/85/01-Analysis-of-Algorithms-Introduction-73-320.jpg)
![Counting the Operations
Insertion Sort(A) length(A):=N
1 for j← 2 to length(A)
2 do
3 key ← A[j]
4 Insert A[j] into the sorted sequence A[1, ..., j − 1]}
5 i ← j − 1
6 while i > 0 and A[i] > key
7 do
8 A[i + 1] ← A[i]
9 i ← i − 1
10 A[i + 1] ← key
Count Value
c4
N
j=2 j
31 / 36](https://image.slidesharecdn.com/01introductionslideshare-150316145938-conversion-gate01/85/01-Analysis-of-Algorithms-Introduction-74-320.jpg)
![Counting the Operations
Insertion Sort(A) length(A):=N
1 for j← 2 to length(A)
2 do
3 key ← A[j]
4 Insert A[j] into the sorted sequence A[1, ..., j − 1]}
5 i ← j − 1
6 while i > 0 and A[i] > key
7 do
8 A[i + 1] ← A[i]
9 i ← i − 1
10 A[i + 1] ← key
Count Value
c5
N
j=2(j − 1)
31 / 36](https://image.slidesharecdn.com/01introductionslideshare-150316145938-conversion-gate01/85/01-Analysis-of-Algorithms-Introduction-75-320.jpg)
![Counting the Operations
Insertion Sort(A) length(A):=N
1 for j← 2 to length(A)
2 do
3 key ← A[j]
4 Insert A[j] into the sorted sequence A[1, ..., j − 1]}
5 i ← j − 1
6 while i > 0 and A[i] > key
7 do
8 A[i + 1] ← A[i]
9 i ← i − 1
10 A[i + 1] ← key
Count Value
c6
N
j=2(j − 1)
31 / 36](https://image.slidesharecdn.com/01introductionslideshare-150316145938-conversion-gate01/85/01-Analysis-of-Algorithms-Introduction-76-320.jpg)
![Counting the Operations
Insertion Sort(A) length(A):=N
1 for j← 2 to length(A)
2 do
3 key ← A[j]
4 Insert A[j] into the sorted sequence A[1, ..., j − 1]}
5 i ← j − 1
6 while i > 0 and A[i] > key
7 do
8 A[i + 1] ← A[i]
9 i ← i − 1
10 A[i + 1] ← key
Count Value
c7(N − 1)
31 / 36](https://image.slidesharecdn.com/01introductionslideshare-150316145938-conversion-gate01/85/01-Analysis-of-Algorithms-Introduction-77-320.jpg)






![The Worst and The Average
1 The Worst Case
2 The Average
Case
Average Sequence
In the case of insertion sort,
when half of the elements of
A[1, 2, ..., j − 1] are less than
A[j] and half are greater.
Then, there is only the need to
check half of the elements i.e.
j
2.
35 / 36](https://image.slidesharecdn.com/01introductionslideshare-150316145938-conversion-gate01/85/01-Analysis-of-Algorithms-Introduction-85-320.jpg)



