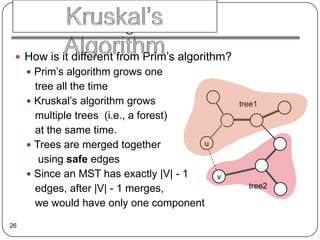
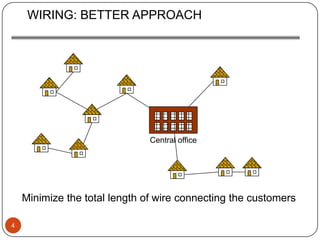
Kruskal's algorithm finds a minimum spanning tree by growing it from a forest of trees. It works by repeatedly selecting the lowest cost edge that connects two different trees without forming a cycle and adding it to the spanning tree. This continues until only one tree remains, which is the minimum spanning tree. The algorithm considers edges in order of increasing weight, merging components with safe edges. It runs in O(ElogV) time by using a priority queue to track the lowest cost remaining edge.

1. TOPIC:- Minimum Spanning Tree
1

2. PROBLEM: LAYING TELEPHONE WIRE
Central office
2

3. WIRING: NAÏVE APPROACH
Central office
Expensive!
3

4. WIRING: BETTER APPROACH
Central office
Minimize the total length of wire connecting the customers
4

5. Minimum Spanning Trees
5

6. We are interested in:
Finding a tree T that contains all the
vertices of a graph G spanning tree
and has the least total weight over all
such trees minimum-spanning
tree
(MST)
w(T ) w((v, u))
( v ,u ) T
6

7. Before discuss about MST (minimum
spanning tree) lets get familiar with Graphs.
7

8. • A graph is a finite set of nodes with edges
between nodes.
• Formally, a graph G is a structure (V,E) 1 2
consisting of
– a finite set V called the set of nodes, and 3 4
– a set E that is a subset of VxV. That is, E is a
set of pairs of the form (x,y) where x and y are
nodes in V
8

9. Directed vs. Undirected Graphs
• If the directions of the edges matter, then we
show the edge directions, and the graph is
called a directed graph (or a digraph)
• If the relationships represented by the edges
are symmetric (such as (x,y) is edge if and
only if x is a sibling of y), then we don’t show
the directions of the edges, and the graph is
called an undirected graph.
9

10. SPANNING TREES
Suppose you have a connected undirected
graph
Connected: every node is reachable from every
other node
Undirected: edges do not have an associated
direction
...then a spanning tree of the graph is a
connected subgraph in which there are no
cycles
A connected, Four of the spanning trees of the graph
undirected
graph
10

11. Minimum Spanning Tree (MST)
A minimum spanning tree is a subgraph of an
undirected weighted graph G, such that
• it is a tree (i.e., it is acyclic)
• it covers all the vertices V
– contains |V| - 1 edges
• the total cost associated with tree edges is the
minimum among all possible spanning trees
• not necessarily unique
11

12. APPLICATIONS OF MST
Cancer imaging. The BC Cancer Research Ctr. uses minimum
spanning trees to describe the arrangements of nuclei in skin
cells.
•Cosmology at the University of Kentucky. This group works on
large-scale structure formation, using methods including N-body
simulations and minimum spanning trees.
•Detecting actin fibers in cell images. A. E. Johnson and R. E.
Valdes-Perez use minimum spanning trees for biomedical
image analysis.
•The Euclidean minimum spanning tree mixing model. S.
Subramaniam and S. B. Pope use geometric minimum
spanning trees to model locality of particle interactions in
turbulent fluid flows. The tree structure of the MST permits a
linear-time solution of the resulting particle-interaction matrix.
12

13. •Extracting features from remotely sensed images. Mark Dobie
and co-workers use minimum spanning trees to find road
networks in satellite and aerial imagery.
•Finding quasar superstructures. M. Graham and co-authors use
2d and 3d minimum spanning trees for finding clusters of
quasars and Seyfert galaxies.
•Learning salient features for real-time face verification, K. Jonsson,
J. Matas, and J. Kittler. Includes a minimum-spanning-tree based
algorithm for registering the images in a database of faces.
•Minimal spanning tree analysis of fungal spore spatial patterns, C.
L. Jones, G. T. Lonergan, and D. E. Mainwaring.
13

14. •A minimal spanning tree analysis of the CfA redshift survey. Dan
Lauer uses minimum spanning trees to understand the large-
scale structure of the universe.
•A mixing model for turbulent reactive flows based on Euclidean
minimum spanning trees, S. Subramaniam and S. B. Pope.
•Sausages, proteins, and rho. In the talk announced here, J.
MacGregor Smith discusses Euclidean Steiner tree theory and
describes potential applications of Steiner trees to protein
conformation and molecular modeling.
•Weather data interpretation. The Insight group at Ohio State is
using geometric techniques such as minimum spanning trees to
extract features from large meteorological data sets
14

15. What is a Minimum-Cost Spanning Tree
 For an edge-weighted , connected, undirected graph, G, the total
cost of G is the sum of the weights on all its edges.
 A minimum-cost spanning tree for G is a minimum spanning tree of G
that has the least total cost.
 Example: The graph
Has 16 spanning trees. Some are:
The graph has two minimum-cost spanning trees, each with a cost of 6:

16. HOW CAN WE
GENERATE A MST?
16

17. We have two Ways
to generate a MST
17

18. Prim’s Algorithm
Prim’s algorithm finds a minimum cost spanning tree by
selecting edges from the graph one-by-one as follows:
 It starts with a tree, T, consisting of the starting vertex,
x.
 Then, it adds the shortest edge emanating from x that
connects T to the rest of the graph.
 It then moves to the added vertex and repeats the
process.

19. Prim’s Algorithm
 The edges in set A always form a single tree
 Starts from an arbitrary “root”: VA = {a}
 At each step:
8 7
b c d
 Find a light edge crossing (VA, V - VA) 4 9
2
 Add this edge to A a 11 i 14 e
4
 Repeat until the tree spans all vertices 7 6
8 10
h g 2
f
1
19

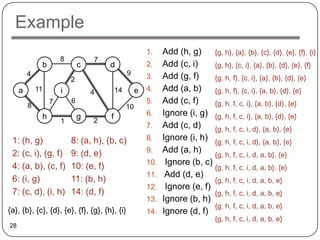
20. Example
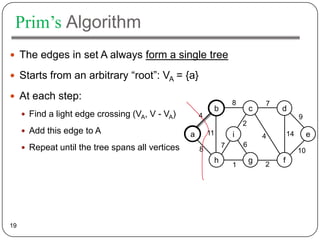
8 7
b c d 0
4 9
2 Q = {a, b, c, d, e, f, g, h, i}
a 11 i 14 e
4 VA =
7 6
8 10 Extract-MIN(Q) a
h g 2
f
1
4
8 7 key [b] = 4 [b] = a
b c d
4 9 key [h] = 8 [h] = a
2
a 11 i 4 14 e
7 6
8 10 4 8
h g 2
f Q = {b, c, d, e, f, g, h, i} VA = {a}
1
8 Extract-MIN(Q) b
20

21. Example
4 8 key [c] = 8 [c] = b
8 7
b c d key [h] = 8 [h] = a - unchanged
4 9
2
8 8
a 11 i 4 14 e
7 6 Q = {c, d, e, f, g, h, i} VA = {a, b}
8 10
h g f Extract-MIN(Q) c
1 2
8
key [d] = 7 [d] = c
4 8 7
8 7 key [f] = 4 [f] = c
b c d
4 2 2 9 key [i] = 2 [i] = c
a 11 i 4 14 e
7 6
8 10 7 4 8 2
h g 2
f Q = {d, e, f, g, h, i} VA = {a, b, c}
1
8 4
21 Extract-MIN(Q) i

22. Example
4 8 7 key [h] = 7 [h] = i
8 7
b c d key [g] = 6 [g] = i
4 9
2 2 7 46 8
a 11 i 4 14 e
Q = {d, e, f, g, h} VA = {a, b, c, i}
7 6
8 10
Extract-MIN(Q) f
h g 2
f
1
8 6 4
7
4 8 7 key [g] = 2 [g] = f
8 7
b c d key [d] = 7 [d] = c unchanged
4 9
2 2 10 key [e] = 10 [e] = f
a 11 i 14 e
4 7 10 2 8
7 6
8 10 Q = {d, e, g, h} VA = {a, b, c, i, f}
h g 2
f
1
6 4
Extract-MIN(Q) g
22 7 2

23. Example
4 8 7 key [h] = 1 [h] = g
8 7
b c d 7 10 1
4 9
2 2 10 Q = {d, e, h} VA = {a, b, c, i, f, g}
a 11 i 4 14 e
7 6
Extract-MIN(Q) h
8 10
h g 2
f
1
7
1 2 4 7 10
4 8 7
8 7
Q = {d, e} VA = {a, b, c, i, f, g, h}
b c d
4 9 Extract-MIN(Q) d
2 2 10
a 11 i 4 14 e
7 6
8 10
h g 2
f
1
23 1 2 4

24. Example
4 8 7
8 7
b c d key [e] = 9 [e] = f
4 9 9
2 2 10
9
a 11 i 4 14 e
7 6 Q = {e} VA = {a, b, c, i, f, g, h, d}
8 10
h g f Extract-MIN(Q) e
1 2
1 2 4 Q= VA = {a, b, c, i, f, g, h, d, e}
24

25. Prim’s (V, E, w, r)
1. Q←
Total time: O(VlgV + ElgV) = O(ElgV)
2. for each u V
3. do key[u] ← ∞ O(V) if Q is implemented
as a min-heap
4. π[u] ← NIL
5. INSERT(Q, u)
O(lgV)
6. DECREASE-KEY(Q, r, 0) key[r] ← 0
Min-heap
7. while Q Executed |V| times
operations:
8. do u ← EXTRACT-MIN(Q) Takes O(lgV) O(VlgV)
Executed O(E) times total
9. for each v Adj[u]
Constant O(ElgV)
10. do if v Q and w(u, v) < key[v]
Takes O(lgV)
11. then π[v] ← u
12. DECREASE-KEY(Q, v, w(u, v))
25

26. Algorithm
 How is it different from Prim’s algorithm?
 Prim’s algorithm grows one
tree all the time
 Kruskal’s algorithm grows tree1
multiple trees (i.e., a forest)
at the same time.
 Trees are merged together u
using safe edges
 Since an MST has exactly |V| - 1 v
edges, after |V| - 1 merges, tree2
we would have only one component
26

27. Kruskal’s Algorithm
8 7
 Start with each vertex being its b c d
4 9
own component 2
a 11 i 4 14 e
 Repeatedly merge two 6
7
8 10
components into one by
h g 2
f
1
choosing the light edge that
We would add
connects them
edge (c, f)
 Which components to consider
at each iteration?
 Scan the set of edges in
monotonically increasing order by
weight
27

28. Example
1. Add (h, g) {g, h}, {a}, {b}, {c}, {d}, {e}, {f}, {i}
8 7
b c d 2. Add (c, i) {g, h}, {c, i}, {a}, {b}, {d}, {e}, {f}
4 9 3. Add (g, f)
2 {g, h, f}, {c, i}, {a}, {b}, {d}, {e}
a 11 i 4 14 e 4. Add (a, b) {g, h, f}, {c, i}, {a, b}, {d}, {e}
8
7 6 5. Add (c, f) {g, h, f, c, i}, {a, b}, {d}, {e}
10
h g f 6. Ignore (i, g) {g, h, f, c, i}, {a, b}, {d}, {e}
1 2
7. Add (c, d) {g, h, f, c, i, d}, {a, b}, {e}
1: (h, g) 8: (a, h), (b, c) 8. Ignore (i, h) {g, h, f, c, i, d}, {a, b}, {e}
2: (c, i), (g, f) 9: (d, e) 9. Add (a, h)
{g, h, f, c, i, d, a, b}, {e}
4: (a, b), (c, f) 10: (e, f) 10. Ignore (b, c)
{g, h, f, c, i, d, a, b}, {e}
11. Add (d, e)
6: (i, g) 11: (b, h) {g, h, f, c, i, d, a, b, e}
12. Ignore (e, f)
7: (c, d), (i, h) 14: (d, f) {g, h, f, c, i, d, a, b, e}
13. Ignore (b, h)
{g, h, f, c, i, d, a, b, e}
{a}, {b}, {c}, {d}, {e}, {f}, {g}, {h}, {i} 14. Ignore (d, f)
{g, h, f, c, i, d, a, b, e}
28

29. Thank You
 Bibliography-
 http://www.cs.brown.edu/
 en.wikipedia.org/wiki/
29