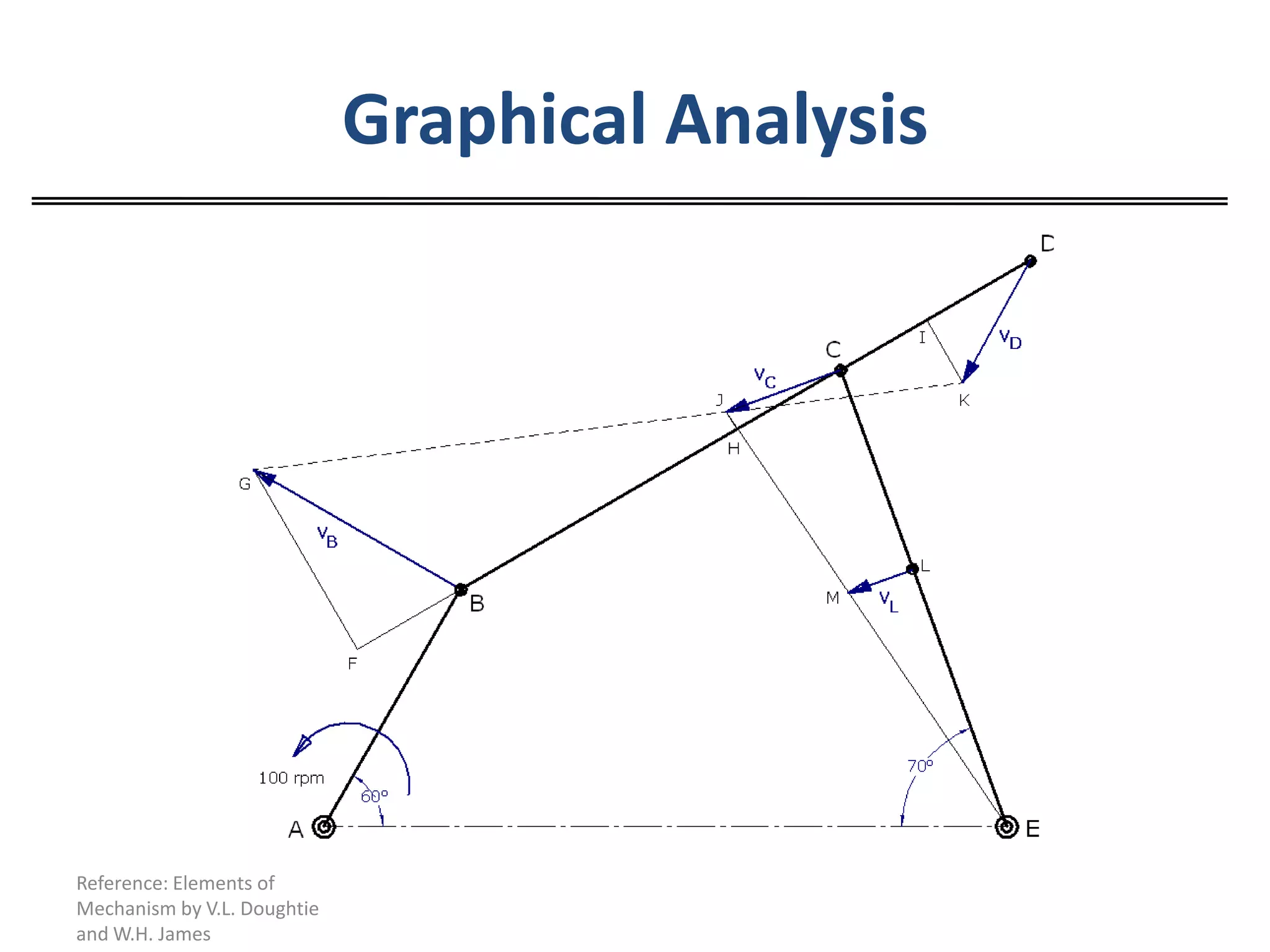
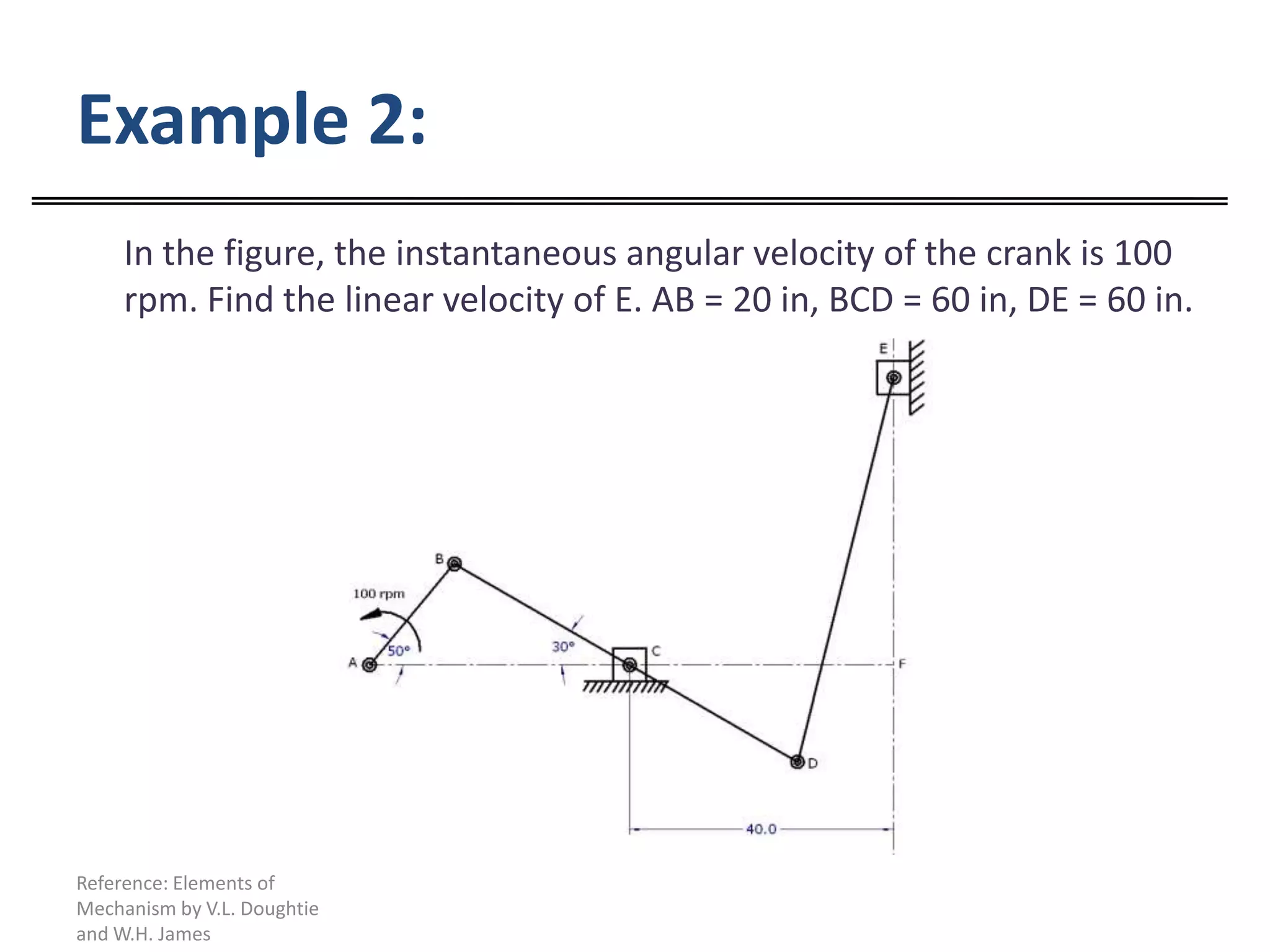
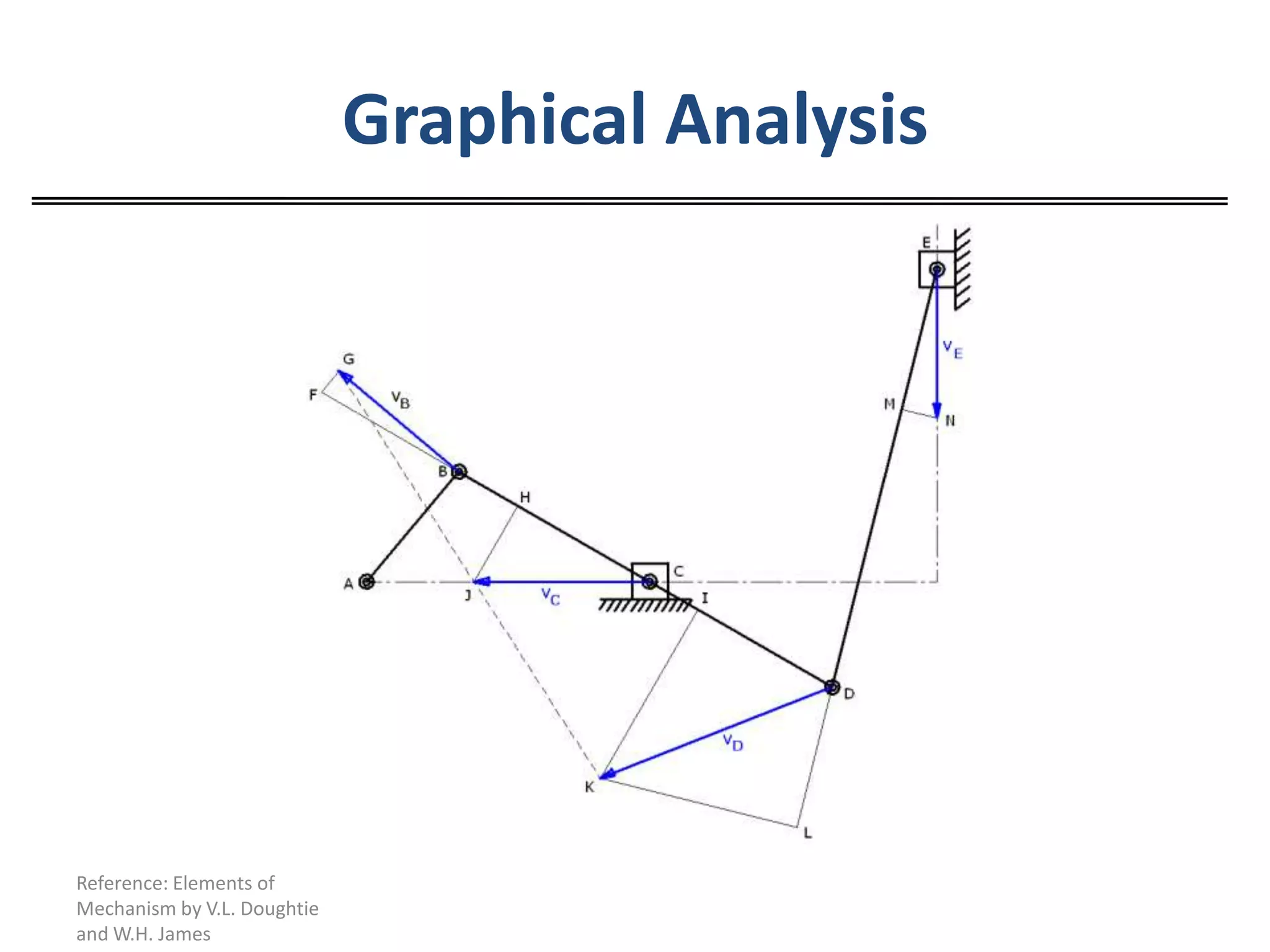
The document discusses resolving velocities into components and calculating velocities at different points on a body. It provides two examples of using graphical analysis to calculate velocities at points on linkages, where the angular velocity of a crank is given. The examples demonstrate resolving velocities into components along and perpendicular to lines connecting points to determine individual point velocities.

1. Velocities by Resolution and
Composition
Lecture Notes
Reference: Elements of
Mechanism by V.L. Doughtie
and W.H. James

2. Resolution and Composition
If the velocity of one point and the direction
of the velocity of any point on a body are
known, the velocity of any other point on that
body may be obtained by resolving the known
velocity vector into components along and
perpendicular to the line joining these points
and making one of the velocity of the other
point equal to the component along the line.
Reference: Elements of
Mechanism by V.L. Doughtie
and W.H. James

3. Example 1:
In the link shown below, the instantaneous angular velocity of the crank
AB is 100 rpm counter clockwise. AB = 25 in, 60 deg with respect to the
horizontal, BC = 40 in, CD = 20 in, CE is 70 deg with respect to the
horizontal. Calculate the velocity B, C, D and L
Reference: Elements of
Mechanism by V.L. Doughtie
and W.H. James

4. Graphical Analysis
Reference: Elements of
Mechanism by V.L. Doughtie
and W.H. James

5. Graphical Analysis
Reference: Elements of
Mechanism by V.L. Doughtie
and W.H. James

6. Example 2:
In the figure, the instantaneous angular velocity of the crank is 100
rpm. Find the linear velocity of E. AB = 20 in, BCD = 60 in, DE = 60 in.
Reference: Elements of
Mechanism by V.L. Doughtie
and W.H. James

7. Graphical Analysis
Reference: Elements of
Mechanism by V.L. Doughtie
and W.H. James

8. Graphical Analysis
Reference: Elements of
Mechanism by V.L. Doughtie
and W.H. James

9. Reference:
Elements of Mechanism by V.L. Doughtie and
W.H. James. © 1954 by John and Wiley and
Sons, Inc. Page 41 - 48.
Reference: Elements of
Mechanism by V.L. Doughtie
and W.H. James