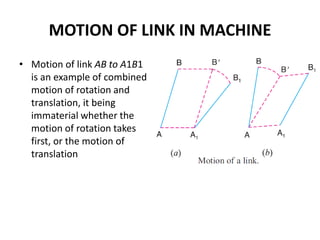
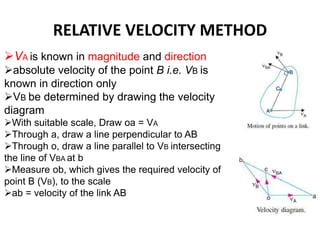
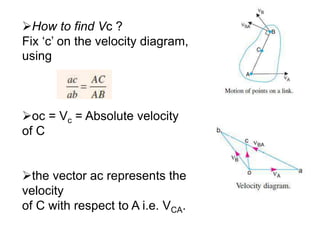
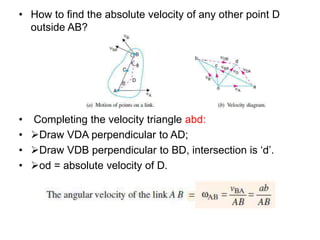
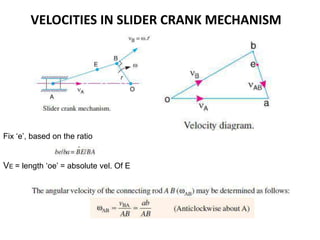
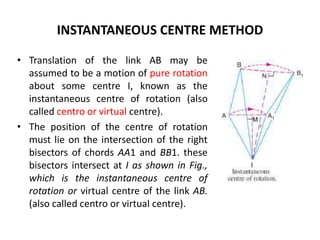
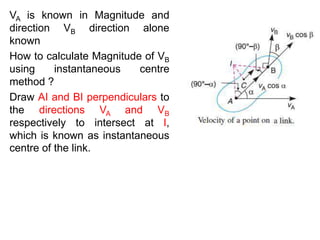
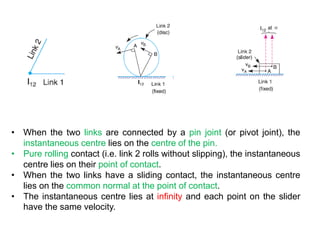
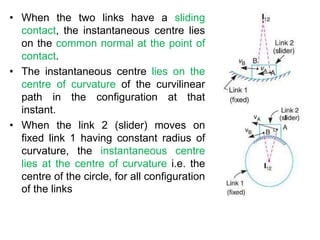
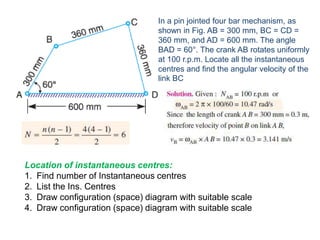
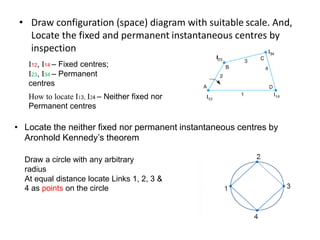
1. Two methods are described for determining the velocity of points on moving links: the relative velocity method and instantaneous center method. 2. The relative velocity method constructs velocity triangles to find velocities. It can be used for any linkage configuration. 3. The instantaneous center method assumes the link rotates about a single center, making it easier for simple mechanisms. This center lies at intersections of bisectors. 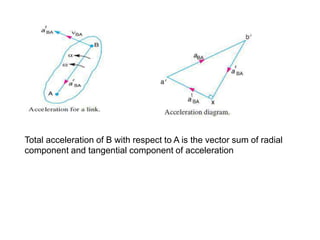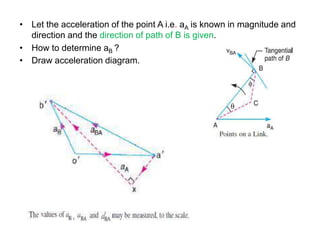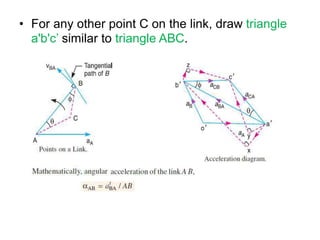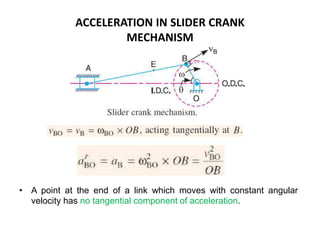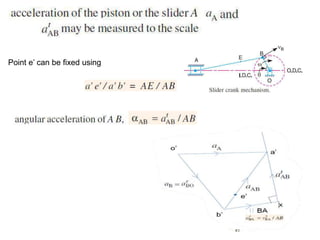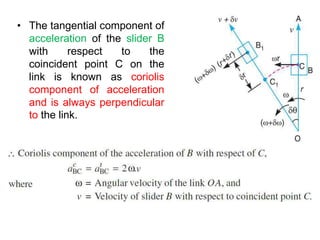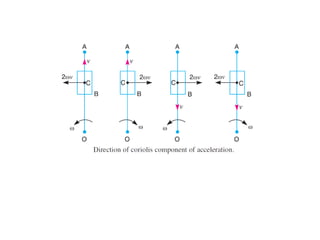4. Acceleration analysis considers centripetal and tangential components. Total acceleration is the vector sum of these components. Acceleration diagrams can be constructed similarly to velocity diagrams.

1. Module 2
Velocity and acceleration analysis of
mechanism

2. MOTION OF LINK IN MACHINE
• Motion of link AB to A1B1
is an example of combined
motion of rotation and
translation, it being
immaterial whether the
motion of rotation takes
first, or the motion of
translation

3. METHODS FOR DETERMINING THE VELOCITY
OF A POINT ON A LINK
1. Relative velocity method
• Can be used in any configuration
2. Instantaneous centre method
• convenient and easy to apply in simple mechanisms

4. RELATIVE VELOCITY METHOD

6. MOTION OF A LINK
Let one of the extremities (B) of the link move
relative to A, in a clockwise direction.
No relative motion between A and B, along
the line AB
relative motion of B with respect to A must be
perpendicular to AB.
Hence velocity of any point on a link with respect to
another point on the
same link is always perpendicular to the line joining
these points on the
configuration (or space) diagram.

8. RELATIVE VELOCITY METHOD
VA is known in magnitude and direction
absolute velocity of the point B i.e. VB is
known in direction only
VB be determined by drawing the velocity
diagram
With suitable scale, Draw oa = VA
Through a, draw a line perpendicular to AB
Through o, draw a line parallel to VB intersecting
the line of VBA at b
Measure ob, which gives the required velocity of
point B (VB), to the scale
ab = velocity of the link AB

9. How to find Vc ?
Fix ‘c’ on the velocity diagram,
using
oc = Vc = Absolute velocity
of C
the vector ac represents the
velocity
of C with respect to A i.e. VCA.

10. • How to find the absolute velocity of any other point D
outside AB?
• Completing the velocity triangle abd:
• Draw VDA perpendicular to AD;
• Draw VDB perpendicular to BD, intersection is ‘d’.
• od = absolute velocity of D.

11. VELOCITIES IN SLIDER CRANK MECHANISM
Fix ‘e’, based on the ratio
VE = length ‘oe’ = absolute vel. Of E

12. RUBBING VELOCITY AT A PIN JOINT
• The rubbing velocity is defined as the algebraic sum
between the angular velocities of the two links which are
connected by pin joints, multiplied by the radius of the pin.

13. INSTANTANEOUS CENTRE METHOD
• Translation of the link AB may be
assumed to be a motion of pure rotation
about some centre I, known as the
instantaneous centre of rotation (also
called centro or virtual centre).
• The position of the centre of rotation
must lie on the intersection of the right
bisectors of chords AA1 and BB1. these
bisectors intersect at I as shown in Fig.,
which is the instantaneous centre of
rotation or virtual centre of the link AB.
(also called centro or virtual centre).

14. VA is known in Magnitude and
direction VB direction alone
known
How to calculate Magnitude of VB
using instantaneous centre
method ?
Draw AI and BI perpendiculars to
the directions VA and VB
respectively to intersect at I,
which is known as instantaneous
centre of the link.

15. • Since A and B are the points on a rigid link, there
cannot be any relative motion between them along
the line AB.

16. If VA is known in magnitude and direction and VB in direction
only, then velocity of point B or any other point C lying on the
same link may be determined (Using iv) in magnitude and
direction.

18. • When the two links are connected by a pin joint (or pivot joint), the
instantaneous centre lies on the centre of the pin.
• Pure rolling contact (i.e. link 2 rolls without slipping), the instantaneous
centre lies on their point of contact.
• When the two links have a sliding contact, the instantaneous centre
lies on the common normal at the point of contact.
• The instantaneous centre lies at infinity and each point on the slider
have the same velocity.

19. • When the two links have a sliding
contact, the instantaneous centre lies
on the common normal at the point of
contact.
• The instantaneous centre lies on the
centre of curvature of the curvilinear
path in the configuration at that
instant.
• When the link 2 (slider) moves on
fixed link 1 having constant radius of
curvature, the instantaneous centre
lies at the centre of curvature i.e. the
centre of the circle, for all configuration
of the links

20. ARONHOLD KENNEDY (OR THREE
CENTRES IN LINE) THEOREM
• It states that if three bodies move relatively to each other, they have
three instantaneous centres and lie on a straight line.

21. In a pin jointed four bar mechanism, as
shown in Fig. AB = 300 mm, BC = CD =
360 mm, and AD = 600 mm. The angle
BAD = 60°. The crank AB rotates uniformly
at 100 r.p.m. Locate all the instantaneous
centres and find the angular velocity of the
link BC
Location of instantaneous centres:
1. Find number of Instantaneous centres
2. List the Ins. Centres
3. Draw configuration (space) diagram with suitable scale
4. Draw configuration (space) diagram with suitable scale

22. • Draw configuration (space) diagram with suitable scale. And,
Locate the fixed and permanent instantaneous centres by
inspection
I12, I14 – Fixed centres;
I23, I34 – Permanent
centres
How to locate I13, I24 – Neither fixed nor
Permanent centres
• Locate the neither fixed nor permanent instantaneous centres by
Aronhold Kennedy’s theorem
Draw a circle with any arbitrary
radius
At equal distance locate Links 1, 2, 3 &
4 as points on the circle

23. ACCELERATION IN MECHANISMS
Acceleration analysis plays a very important role in the development of
machines and mechanisms
Let the point B moves with respect to A, with an
angular velocity of ω rad/s and let α rad/s2 be the
angular acceleration of the link AB.
1. The centripetal or radial component of acceleration,
which is perpendicular to the velocity (i.e. parallel to link
AB) of the particle at the given instant.
2. The tangential component, which is parallel to the velocity (i.e.
Perpendicular to Link AB) of the particle at the given instant.

24. Total acceleration of B with respect to A is the vector sum of radial
component and tangential component of acceleration

25. • Let the acceleration of the point A i.e. aA is known in magnitude and
direction and the direction of path of B is given.
• How to determine aB ?
• Draw acceleration diagram.

26. • For any other point C on the link, draw triangle
a'b'c’ similar to triangle ABC.

27. ACCELERATION IN SLIDER CRANK
MECHANISM
• A point at the end of a link which moves with constant angular
velocity has no tangential component of acceleration.

28. Point e’ can be fixed using

29. CORIOLIS COMPONENT OF ACCELERATION
• When a point on one link is sliding along another rotating link, such
as in quick return motion mechanism

30. • The tangential component of
acceleration of the slider B
with respect to the
coincident point C on the
link is known as coriolis
component of acceleration
and is always perpendicular
to the link.