Recommended
PDF
PRML上巻勉強会 at 東京大学 資料 第1章後半
PDF
PDF
PPTX
PDF
PDF
PDF
PPTX
PDF
PDF
[PRML] パターン認識と機械学習(第2章:確率分布)
PDF
PRML上巻勉強会 at 東京大学 資料 第1章前半
PDF
PDF
PPTX
パターン認識と機械学習(PRML)第2章 確率分布 2.3 ガウス分布
ZIP
PDF
PDF
2013.12.26 prml勉強会 線形回帰モデル3.2~3.4
PDF
PPTX
PDF
PDF
PDF
PDF
Prml4.4 ラプラス近似~ベイズロジスティック回帰
PPTX
PDF
PDF
PRML上巻勉強会 at 東京大学 資料 第2章2.3.3 〜 2.5.2
PDF
[PRML] パターン認識と機械学習(第1章:序論)
PDF
「3.1.2最小二乗法の幾何学」PRML勉強会4 @筑波大学 #prml学ぼう
PDF
PPTX
More Related Content
PDF
PRML上巻勉強会 at 東京大学 資料 第1章後半
PDF
PDF
PPTX
PDF
PDF
PDF
PPTX
What's hot
PDF
PDF
[PRML] パターン認識と機械学習(第2章:確率分布)
PDF
PRML上巻勉強会 at 東京大学 資料 第1章前半
PDF
PDF
PPTX
パターン認識と機械学習(PRML)第2章 確率分布 2.3 ガウス分布
ZIP
PDF
PDF
2013.12.26 prml勉強会 線形回帰モデル3.2~3.4
PDF
PPTX
PDF
PDF
PDF
PDF
Prml4.4 ラプラス近似~ベイズロジスティック回帰
PPTX
PDF
PDF
PRML上巻勉強会 at 東京大学 資料 第2章2.3.3 〜 2.5.2
PDF
[PRML] パターン認識と機械学習(第1章:序論)
PDF
「3.1.2最小二乗法の幾何学」PRML勉強会4 @筑波大学 #prml学ぼう
Similar to PRML 1.6 情報理論
PDF
PPTX
PDF
【Unity道場】ゲーム制作に使う数学を学習しよう
PDF
PDF
PDF
PDF
PDF
ブラック ショールズの方程式の解法 フーリエ級数と熱伝導方程式一 1st Edition すずきたろう
PPT
PPT
PDF
PRML輪講用資料10章(パターン認識と機械学習,近似推論法)
PPTX
PDF
Introduction to the particle filter
PDF
PDF
PDF
PPTX
PDF
Information geometry chap6
PPTX
Text classification zansa
PDF
2014年度秋学期 応用数学(解析) 第1部・「無限」の理解 / 第2回 無限にも大小がある (2014. 10. 2)
More from sleepy_yoshi
PDF
PDF
PDF
計算論的学習理論入門 -PAC学習とかVC次元とか-
PDF
PDF
PDF
ICML2013読み会: Distributed training of Large-scale Logistic models
PDF
PRML復々習レーン#10 7.1.3-7.1.5
PDF
PDF
PDF
SEXI2013読み会: Adult Query Classification for Web Search and Recommendation
PDF
ICML2012読み会 Scaling Up Coordinate Descent Algorithms for Large L1 regularizat...
PDF
SIGIR2012勉強会 23 Learning to Rank
PDF
PDF
DSIRNLP#3 LT: 辞書挟み込み型転置インデクスFIg4.5
PDF
PDF
KDD2013読み会: Direct Optimization of Ranking Measures
PDF
PDF
PDF
KDD2014勉強会: Large-Scale High-Precision Topic Modeling on Twitter
PDF
Recently uploaded
PDF
TomokaEdakawa_職種と講義の関係推定に基づく履修支援システムの基礎検討_HCI2026
PDF
maisugimoto_曖昧さを含む仕様書の改善を目的としたアノテーション支援ツールの検討_HCI2025.pdf
PDF
20260119_VIoTLT_vol22_kitazaki_v1___.pdf
PDF
第21回 Gen AI 勉強会「NotebookLMで60ページ超の スライドを作成してみた」
PDF
アジャイル導入が止まる3つの壁 ─ 文化・他部門・組織プロセスをどう乗り越えるか
PDF
Starlink Direct-to-Cell (D2C) 技術の概要と将来の展望
PDF
ST2024_PM1_2_Case_study_of_local_newspaper_company.pdf
PDF
Team Topology Adaptive Organizational Design for Rapid Delivery of Valuable S...
PRML 1.6 情報理論 1. PRML読書会第1回
1.6
2010-05-01
SUHARA YOSHIHIKO
id:sleepy_yoshi
2. 3. 4. 情報 の定義
• p(x) の情報 h(x)
– (1) h(x) は p(x) の単調減少関数
• しい出 事の方が「 きの 合い」が大きい
– (2) h(x,y) = h(x) + h(y)
• 情報の加法性
上記を満たす関数 ⇒ 対数のみ (演習1.28)
h( x) = − log 2 p( x) (1.92)
ここでいう情報 はあくまで
情報 (information theory) における約束事
3
5. 6. 7. 8. ___
/ \
/ノ \ u. \ !?
/ (●) (●) \
| (__人__) u. |
\ u.` ⌒´ /
ノ \
/´ ヽ
____
/ \!??
/ u ノ \
/ u (●) \
| (__人__)|
\ u .` ⌒/
ノ \
/´ ヽ
7
9. 10. 演習1.28
• h(p2) = h(p p) = h(p) + h(p) = 2h(p)
• h(pk+1) = h(pk p) = h(pk) + h(p)
= k h(p) + h(p) = (k + 1) h(p)
• h(pn/m) = n h(p1/m) = m・n/m h(p1/m)
= n/m h(pm/m) = n/m h(p)
ここでp=qx
h( p ) h( q x ) xh(q) h(q)
= x
= =
ln( p) ln(q ) x ln(q) ln(q)
h( p) : h(q) = ln( p) : ln(q) ∴ h( p) ∝ ln( p) 9
11. よって
対数で表現される!
____
/ \ /\ キリッ
. / (ー) (ー)\
/ ⌒(__人__)⌒ \
| |r┬-| |
\ `ー’´ /
ノ \
/´ ヽ
| l \
ヽ -一””””~~``’ー?、 -一”””’ー-、.
ヽ ____(⌒)(⌒)⌒) ) (⌒_(⌒)⌒)⌒))
10
12. 13. 14. エントロピーの定義
• エントロピー: 情報の平均
– 情報 (1.92)の期待値
H[ x] = −∑ p ( x) log 2 p( x) (1.93)
x
ただし,lim p →0 p ln p = 0 より
p ( x) = 0 のとき p ( x) ln p( x) = 0
13
15. エントロピーの
• 1)
– 8個の状態を等 で取る 変数xの場合
1 1
H[ x] = −8 × log 2 = 3bit
8 8
• 2)
– 8個の状態 {a,b,c,d,e,f,g,h}
– は (1/2, 1/4, 1/8, 1/16, 1/64, 1/64, 1/64, 1/64)
1 1 1 1 1 1 1 1 4 4
H[ x] = − log 2 − log 2 − log 2 − log 2 − log 2 = 2bit
2 2 4 4 8 8 16 16 64 64
非一様な分布のエントロピーは,
一様な分布のエントロピーより小さい 14
16. 符号化におけるエントロピーの解釈
• 変数がどの状態にあるかを受信者に伝えたい
– (非一様の分布の場合) よく起きる事象に短い符号を,
ま 起きない事象に い符号を使うことで,符号
の平均を短くできる
• 2)の場合
– {a,b,c,d,e,f,g,h}に対し,符号偱 (0, 10, 110, 1110,
111100, 11101, 111110, 11111) を割り当てる
1 1 1 1 1
平均符号長 = ×1 + × 2 + × 3 + × 4 + 4 × × 6 = 2bit
2 4 8 16 64
変数のエントロピーと同じ
⇒ イ なし符号化 (noiseless coding theorem) 15
17. 18. エントロピーの別の解釈 (1/2)
• 同じ物体を箱に分けて入れる問題
– N個の物体をたくさんの箱に分けて入れる
– i番目の箱にはni個の物体が存在
– N個の物体を箱に入れる方法: N!通り
– i番目の箱に物体を入れた順番: ni!通り ←区別しない
⇒ N個の物体の箱への入れ方の総数 ( ) は,
!
W= (1.94)
∏i ni !
17
19. エントロピーの別の解釈 (2/2)
• エントロピーを多 の対数を適当に定数 し
たものと定義
1 1 1
H= ln W = ln !− ∑ ln n !
i
i (1.95)
スターリングの近似式 ln !≅ ln − と ∑n
i i = より
ni ni
H = lim ∑ ln = −∑ pi ln pi (1.97)
i
→∞
i
箱は 偶 変数Xの状態xiと解釈でき,p(X=xi) = piとすると
H [ p] = −∑ p( xi ) ln p( xi ) (1.98)18
i
20. 21. 22. エントロピーの最大化 (1/2)
• ラグランジュ乗数法を使って最大値を求める
– の総和は1という制約を入れる
~
H = −∑ p ( xi ) ln p ( xi ) + λ ∑ p( xi ) − 1 (1.99)
i i
∂
− ∑ p( xi ) ln p ( xi ) + λ ∑ p( xi ) − 1 = 0
∂p ( xk ) i
i
− (ln p ( xk ) + 1) + λ = 0
p(xi) が全て等しいとき (p(xi) = 1/M) 最大化
最大値はln M 21
23. 24. 補足: ラグランジュ乗数法
• 制約付き非線形最適化の常套手段 (詳しくは付録E)
• g(x) = 0 の制約において f(x) を最適化
⇒ 以下で定義されるラグランジュ関数の停 点を求める
L ( x, λ ) ≡ f ( x ) + λ g ( x )
すなわち
∇f ( x ) + λ ∇g ( x ) = 0
23
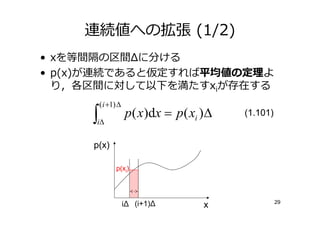
25. 26. 27. 28. 29. 30. 31. 連続値への拡張 (2/2)
• Σp(xi)Δ=1 が り つので
H ∆ = −∑ p ( xi )∆ ln( p ( xi )∆)
i
= −∑ p ( xi )∆ ln p ( xi ) − ∑ p ( xi )∆ ln ∆
i i
= −∑ p ( xi )∆ ln p ( xi ) − ln ∆ (1.102)
i
• 第2項のlnΔを無視してΔ→0の極限を考える
– 第1項はp(x)ln p(x) に収束
lim− ∑ p ( xi )∆ ln p( xi ) = − ∫ p ( x) ln p ( x)dx (1.103)
∆ →0
i 微分エントロピー
30
32. 連続値への拡張 (2/2)
• Σp(xi)Δ=1 が り つので
H ∆ = −∑ p ( xi )∆ ln( p ( xi )∆) 連続変数を厳密に規
i 定するために無限
= −∑ p ( xi )∆ ln p ( xi ) − ∑ p (ビット数が必要であ
xi )∆ ln ∆
ることを反映
i i
= −∑ p ( xi )∆ ln p ( xi ) − ln ∆ (1.102)
i
• 第2項のlnΔを無視してΔ→0の極限を考える
– 第1項はp(x)ln p(x) に収束
lim− ∑ p ( xi )∆ ln p( xi ) = − ∫ p ( x) ln p ( x)dx (1.103)
∆ →0
i 微分エントロピー
31
33. 微分エントロピーの最大化 (1/2)
H[x] = − ∫ p (x) ln p (x)dx (1.104)
連続変数の場合のエントロピー最大化を考える.
以下の3つの制約のもとで最大化
∞
規格化 ∫ p ( x ) dx = 1 (1.105)
−∞
∞
分布の平均 ∫ xp( x)dx = µ (1.106)
−∞
∞
分布の広がり ∫ ( x − µ ) 2 p ( x ) dx = σ 2 (1.107)
−∞
ラグランジュ関数=
∞
∞ p ( x)dx − 1
− ∫ p ( x) ln p ( x)dx +λ1 ∫
−∞ −∞
∞ xp( x)dx − µ + λ ∞ ( x − µ ) 2 p ( x)dx − σ 2
+ λ2 ∫ 3 ∫−∞ 32
−∞
34. 35. 微分エントロピーの最大化 (2/2)
• 以下の結果が得られる (演習1.34)
⇒ 微分エントロピーを最大化する分布はガウス分布
1 ( x − µ )2
p( x) = exp− (1.109)
(2πσ 2 )1/ 2 2σ
2
非負制約を設けなかったけれど,結果オーライ
ガウス分布の微分エントロピーは以下になる (演習1.35)
H [ x] =
1
2
{1 + ln(2πσ 2 ) } (1.110)
σ2が増えて分布が幅広くなるにつれて大きくなる
> 2πσ 2 のとき,H[x] < 0 となる
1
e 34
36. 条件付きエントロピー
• 同時分布 p(x,y) を考える
• xの値が既知とすれば,対応するyの値を特定す
るために必要な情報は- ln p(y|x)
• したがって,yを特定するために必要な情報の平
均は,
H[y | x] = − ∫∫ p(y, x) ln p(y | x)dydx (1.111)
これをxに対するyの条件付きエントロピーと呼ぶ
35
37. 38. 39. 相対エントロピー
• 未知の分布 p(x) を近似的に q(x) でモデル化
– q(x) を用いて
– xの値を特定するために必要な 加情報 の平均は
(
KL( p || q) = − ∫ p(x) ln q (x)dx − − ∫ p(x) ln p(x)dx )
q ( x)
= − ∫ p(x) ln dx (1.113)
p ( x)
この値は,カルバック-ライブラーダイバージェンス (KLd)
または 相対エントロピーと呼ばれる
注意: KL( p || q) ≠ KL(q || p) 38
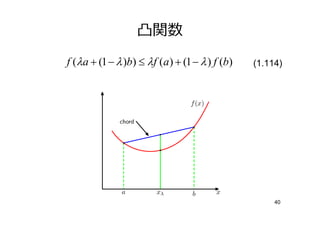
40. 41. 凸関数
f (λa + (1 − λ )b) ≤ λf (a) + (1 − λ ) f (b) (1.114)
40
42. 43. イ ンセンの 等式
• (1.114)を任意の点集合へ拡張した(1.115)は,
イェン ンの と呼ばれる (演習1.38)
M M
f ∑ λi xi ≤ ∑ λi f ( xi ) (1.115)
i =1 i =1
ここで λi ≥ 0 ∑λ
i i =1
λi を 変数x上の 分布と なすと
f (E[ x]) ≤ E[ f ( x)] (1.116)
連続変数に対しては,
f (∫ xp(x)dx) ≤ ∫ f (x) p(x)dx (1.117)
42
44. KLdの解釈
• イ ンセンの 等式をKLdへ適用
– ln(x) が凸関数であることを 用
q ( x)
KL( p || q) = − ∫ p (x) ln dx ≥ − ln ∫ q(x)dx = 0
p ( x) (1.118)
等号は全てのxについてq(x) = p(x) のとき り つので
KLdは2つの分布 p(x)とq(x) の隔たりを表していることがわかる
43
45. KLdの最小化 ⇒ ?!
• 未知の 分布のモデル化の問題
– データが未知の分布 p(x) からサンプルされる
– 可変なパラメータθを持つ分布 q(x|θ) を用いて近似
– θを決める方法
⇒ p(x) と p(x|θ) のKLdをθについて最小化
• p(x) はわからないので,xnの有限和で近似 ((1.35)式)
1
KL( p || q ) ≈ ∑ {− ln q(x
n =1
n | θ ) + ln p (x n )}
KLdの最小化 ⇒ の最大化
44
46. 再掲: 演習1.29
• エントロピー最大化をJensenの 等式から く
• 解)
M
1
H [ x] = ∑ p ( xi ) ln
i p ( xi )
ln(x)は凹関数なので,Jensenの 等式より
M 1
H [ x] ≤ ln ∑ p ( xi )
= ln M
i p ( xi )
45
47. 48. 相僆情報
• 同時分布 p(x, y) を考える
• たつの 変数が の場合 p(x,y)=p(x)p(y)
• 変数同士の「近さ」を測るために,同時分布と周
辺分布の積のKLdを考える
I[x, y ] ≡ KL( p (x, y ) || p (x) p (y ))
p ( x) p ( y )
= − ∫∫ p(x, y ) ln
p(x, y ) dxdy
これを変数x,yの間の相 と呼ぶ
47
49. 相僆情報 とエントロピーの関係
• の加法・乗法定 を用いて以下のとおりに
表すことができる (演習1.41)
I[x, y ] = H[x] − H[x | y ] = H[y ] − H[y | x]
• ベイズの観点からp(x) をxの事前分布,p(x|y)
を新たなデータyを観測した後の事後分布と考え
られる
⇒ 相僆情報 は,新たなyを観測した結果として,
xに関する 実性が減少した 合いを表す
48
50. 演習1.41
• I[x,y] = H[x] – H[x|y] を証明
p ( x) p ( y )
− ∫∫ p (x, y ) ln
p (x, y ) dxdy
p ( x) p ( y )
= − ∫∫ p(x, y ) ln
p (x | y ) p (y ) dxdy
= − ∫∫ p(x, y ) ln p(x)dxdy + ∫∫ p (x, y ) ln p (x | y )dxdy
= − ∫ p (x) ln p(x)dx + ∫∫ p(x, y ) ln p(x | y )dxdy
= H[x] − H[x | y ] 49
51. 52. 53. 54. まとめ
情報 の基 を しました
• 情報
– 情報 における定義
• エントロピー
– 条件付きエントロピー
– 相対エントロピー
• カルバック・ライブラーダイバージェンス
• 相僆情報
おまけあり・・・
53
55. 56. 相僆情報 の応用
• pointwise mutual information (PMI)
– a.k.a. self mutual information (SMI)
– 関連語抽出などに用いられる
p( x) p ( y )
PMI(x = x, y = y ) = − ln
p ( x, y )
• expected mutual information
– PMIは, 語に っ張られる問題があるので,期
待値を取ってあげる
p( x) p( y )
EMI(x = x, y = y ) = − p ( x, y ) ln
p ( x, y )
55
57. 58. 実験: 相僆情報 による関連語の抽
出
• データセット
– 20newsgroups
• 公開データセット
• http://people.csail.mit.edu/jrennie/20Newsgroups/
– ニュースグループの20カテゴリに投稿された記事1000文書ずつ
• 実験
– PMI(カテゴリ,単語),EMI(カテゴリ,単語) を高い順に並べる
alt.atheism sci.crypt
comp.graphics sci.electronics
comp.os.ms-windows.misc sci.med
comp.sys.ibm.pc.hardware sci.space
comp.sys.mac.hardware soc.religion.christian
comp.windows.x talk.politics.guns
misc.forsale talk.politics.mideast
rec.autos talk.politics.misc
rec.motorcycles talk.religion.misc
rec.sport.baseball
57
rec.sport.hockey
59. 60. 61.






![[Shannon 1948]より
6](https://image.slidesharecdn.com/prml16suhara-100510131352-phpapp01/85/PRML-1-6-7-320.jpg)





![エントロピーの定義
• エントロピー: 情報の平均
– 情報 (1.92)の期待値
H[ x] = −∑ p ( x) log 2 p( x) (1.93)
x
ただし,lim p →0 p ln p = 0 より
p ( x) = 0 のとき p ( x) ln p( x) = 0
13](https://image.slidesharecdn.com/prml16suhara-100510131352-phpapp01/85/PRML-1-6-14-320.jpg)
![エントロピーの
• 1)
– 8個の状態を等 で取る 変数xの場合
1 1
H[ x] = −8 × log 2 = 3bit
8 8
• 2)
– 8個の状態 {a,b,c,d,e,f,g,h}
– は (1/2, 1/4, 1/8, 1/16, 1/64, 1/64, 1/64, 1/64)
1 1 1 1 1 1 1 1 4 4
H[ x] = − log 2 − log 2 − log 2 − log 2 − log 2 = 2bit
2 2 4 4 8 8 16 16 64 64
非一様な分布のエントロピーは,
一様な分布のエントロピーより小さい 14](https://image.slidesharecdn.com/prml16suhara-100510131352-phpapp01/85/PRML-1-6-15-320.jpg)



![エントロピーの別の解釈 (2/2)
• エントロピーを多 の対数を適当に定数 し
たものと定義
1 1 1
H= ln W = ln !− ∑ ln n !
i
i (1.95)
スターリングの近似式 ln !≅ ln − と ∑n
i i = より
ni ni
H = lim ∑ ln = −∑ pi ln pi (1.97)
i
→∞
i
箱は 偶 変数Xの状態xiと解釈でき,p(X=xi) = piとすると
H [ p] = −∑ p( xi ) ln p( xi ) (1.98)18
i](https://image.slidesharecdn.com/prml16suhara-100510131352-phpapp01/85/PRML-1-6-19-320.jpg)












![微分エントロピーの最大化 (1/2)
H[x] = − ∫ p (x) ln p (x)dx (1.104)
連続変数の場合のエントロピー最大化を考える.
以下の3つの制約のもとで最大化
∞
規格化 ∫ p ( x ) dx = 1 (1.105)
−∞
∞
分布の平均 ∫ xp( x)dx = µ (1.106)
−∞
∞
分布の広がり ∫ ( x − µ ) 2 p ( x ) dx = σ 2 (1.107)
−∞
ラグランジュ関数=
∞
∞ p ( x)dx − 1
− ∫ p ( x) ln p ( x)dx +λ1 ∫
−∞ −∞
∞ xp( x)dx − µ + λ ∞ ( x − µ ) 2 p ( x)dx − σ 2
+ λ2 ∫ 3 ∫−∞ 32
−∞ ](https://image.slidesharecdn.com/prml16suhara-100510131352-phpapp01/85/PRML-1-6-33-320.jpg)

![微分エントロピーの最大化 (2/2)
• 以下の結果が得られる (演習1.34)
⇒ 微分エントロピーを最大化する分布はガウス分布
1 ( x − µ )2
p( x) = exp− (1.109)
(2πσ 2 )1/ 2 2σ
2
非負制約を設けなかったけれど,結果オーライ
ガウス分布の微分エントロピーは以下になる (演習1.35)
H [ x] =
1
2
{1 + ln(2πσ 2 ) } (1.110)
σ2が増えて分布が幅広くなるにつれて大きくなる
> 2πσ 2 のとき,H[x] < 0 となる
1
e 34](https://image.slidesharecdn.com/prml16suhara-100510131352-phpapp01/85/PRML-1-6-35-320.jpg)
![条件付きエントロピー
• 同時分布 p(x,y) を考える
• xの値が既知とすれば,対応するyの値を特定す
るために必要な情報は- ln p(y|x)
• したがって,yを特定するために必要な情報の平
均は,
H[y | x] = − ∫∫ p(y, x) ln p(y | x)dydx (1.111)
これをxに対するyの条件付きエントロピーと呼ぶ
35](https://image.slidesharecdn.com/prml16suhara-100510131352-phpapp01/85/PRML-1-6-36-320.jpg)
![演習1.37
• H[x,y] = H[y|x] + H[x] を証明せよ
⇒ ホワイトボード
36](https://image.slidesharecdn.com/prml16suhara-100510131352-phpapp01/85/PRML-1-6-37-320.jpg)




![イ ンセンの 等式
• (1.114)を任意の点集合へ拡張した(1.115)は,
イェン ンの と呼ばれる (演習1.38)
M M
f ∑ λi xi ≤ ∑ λi f ( xi ) (1.115)
i =1 i =1
ここで λi ≥ 0 ∑λ
i i =1
λi を 変数x上の 分布と なすと
f (E[ x]) ≤ E[ f ( x)] (1.116)
連続変数に対しては,
f (∫ xp(x)dx) ≤ ∫ f (x) p(x)dx (1.117)
42](https://image.slidesharecdn.com/prml16suhara-100510131352-phpapp01/85/PRML-1-6-43-320.jpg)


![再掲: 演習1.29
• エントロピー最大化をJensenの 等式から く
• 解)
M
1
H [ x] = ∑ p ( xi ) ln
i p ( xi )
ln(x)は凹関数なので,Jensenの 等式より
M 1
H [ x] ≤ ln ∑ p ( xi )
= ln M
i p ( xi )
45](https://image.slidesharecdn.com/prml16suhara-100510131352-phpapp01/85/PRML-1-6-46-320.jpg)

![相僆情報
• 同時分布 p(x, y) を考える
• たつの 変数が の場合 p(x,y)=p(x)p(y)
• 変数同士の「近さ」を測るために,同時分布と周
辺分布の積のKLdを考える
I[x, y ] ≡ KL( p (x, y ) || p (x) p (y ))
p ( x) p ( y )
= − ∫∫ p(x, y ) ln
p(x, y ) dxdy
これを変数x,yの間の相 と呼ぶ
47](https://image.slidesharecdn.com/prml16suhara-100510131352-phpapp01/85/PRML-1-6-48-320.jpg)
![相僆情報 とエントロピーの関係
• の加法・乗法定 を用いて以下のとおりに
表すことができる (演習1.41)
I[x, y ] = H[x] − H[x | y ] = H[y ] − H[y | x]
• ベイズの観点からp(x) をxの事前分布,p(x|y)
を新たなデータyを観測した後の事後分布と考え
られる
⇒ 相僆情報 は,新たなyを観測した結果として,
xに関する 実性が減少した 合いを表す
48](https://image.slidesharecdn.com/prml16suhara-100510131352-phpapp01/85/PRML-1-6-49-320.jpg)
![演習1.41
• I[x,y] = H[x] – H[x|y] を証明
p ( x) p ( y )
− ∫∫ p (x, y ) ln
p (x, y ) dxdy
p ( x) p ( y )
= − ∫∫ p(x, y ) ln
p (x | y ) p (y ) dxdy
= − ∫∫ p(x, y ) ln p(x)dxdy + ∫∫ p (x, y ) ln p (x | y )dxdy
= − ∫ p (x) ln p(x)dx + ∫∫ p(x, y ) ln p(x | y )dxdy
= H[x] − H[x | y ] 49](https://image.slidesharecdn.com/prml16suhara-100510131352-phpapp01/85/PRML-1-6-50-320.jpg)

![補足: 各種エントロピーの関係
• ベン で るとわかり すい
H[X]
H[Y]
H[X|Y] I[X,Y] H[Y|X]
H[X,Y]
51](https://image.slidesharecdn.com/prml16suhara-100510131352-phpapp01/85/PRML-1-6-52-320.jpg)








