JOI夏季セミナーのやつです。

1. 最小全域木
藤原

2. 最小全域木についての探究的課題
• 10章6節。
• 頂点数nの完全無向グラフの各辺に0から1の重
みを一様ランダムにつける。
• 最小全域木の大きさはいくつになるか？
• という問題。

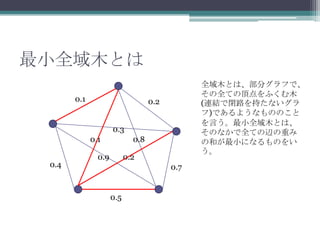
3. 最小全域木とは
全域木とは、部分グラフで、
その全ての頂点をふくむ木
0.1 0.2 (連結で閉路を持たないグラ
フ)であるようなもののこと
を言う。最小全域木とは、
0.3 そのなかで全ての辺の重み
0.1 0.8 の和が最小になるものをい
う。
0.9 0.2
0.4 0.7
0.5

4. 実際にやってみる
• 頂点数|V|=n,辺数|E|=n(n-1)/2.
• プリム法O(Vlog V+E)がよさそう。
• 実際に観察すると長さが10/n以下の辺はほとん
ど使われてなさそう(後述)。長い辺を削除して
も最小全域木は(存在する限り)変わらない。
• →|E|=O(n)まで減らせる。
• →クラスカル法O(E log E)でもよさげ。

5. 実装
• 完全無向グラフKnの各辺0から1の実数の重みを
割り当て。ただしその重みが20/nを超えたとき
はその辺は無視。
• クラスカル。
• 各nについて2^19/n回の平均をとる。

6. 1.4
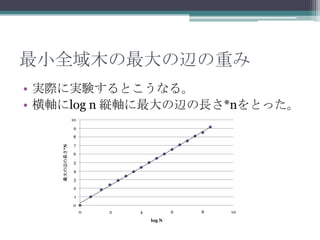
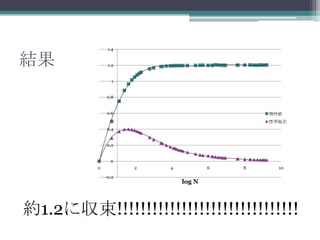
結果 1.2
1
0.8
0.6 期待値
標準偏差
0.4
0.2
0
0 2 4 6 8 10
-0.2
log N
約1.2に収束!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

7. 考察
• 意外なことにnについて増加しなかった。
• 全部でn(n-1)/2の辺があり、全域木を作るのに
必要な辺の数はn-1本。
• →最小全域木では短い方の辺からn-1本とるの
で、辺の長さはO(1/n)くらいで抑えられそう。
• →最小全域木のサイズはO(1)になる。

8. もっと詳しく見積もってみる
• 辺の中でi番目に短いものの長さをXiとする。
• クラスカルでj番目に採用する辺が、何番目に小
さい辺かをYjとする。
• 最小全域木のコストCは以下のようになる。

9. Xについて
• Ｘの期待値E[X]は以下のようになる。
• したがって期待値の線型性とＸとＹが独立であ
ることから、E[C]は次のようになる。

10. Ｙについて
• Ｚjをクラスカルにおいてj-1番目の辺を採用して
からj番目の辺を採用するまでに調べる辺の本数
とする。
• ＹjはZ1からZjまでの和になる。
• すでにn-j+1個のクラスタに分かれているとき、
辺が結ぶ二頂点が別のクラスタに属する(すなわ
ち辺が採用される)確率は(n-j)/(n-j+1)と近似で
きる(たぶん)
• Zjはp=(n-j)/(n-j+1)の幾何確率変数に近似でき
る(おそらく)

11. 幾何分布とは
• 確率pで成功する試行を成功するまで行い続けた
ときの試行回数の分布。
• i回目で初めて成功する確率はp(1-p)^(i-1)
• 期待値は1/p

12. E[C]の計算

13. E[C]の計算
1になった。実際より小さい。
幾何分布の近似のためかと思われる。

14. 最小全域木の最大の辺の重み
最小全域木中の最大の辺の重みを
さっきのモデルで見積もると
しかし実際には……

15. 最小全域木の最大の辺の重み
• 実際に実験するとこうなる。
• 横軸にlog n 縦軸に最大の辺の長さ*nをとった。
10
9
8
7
最大の辺の長さ*N
6
5
4
3
2
1
0
0 2 4 6 8 10
log N

16. 別のアプローチ
• i番目に短い辺がクラスカル法において採用され
る確率をPiとする。期待値の線型性より、
• Piは「頂点数nの完全無向グラフの辺(s,t)以外の
辺からランダムにi-1本の辺を選んだ部分グラフ
において、sとtが連結していない確率」であ
る。
• →計算できそう。

17. 0
0.2
0.4
0.6
0.8
1
1.2
1
21
41
61
81
101
121
141
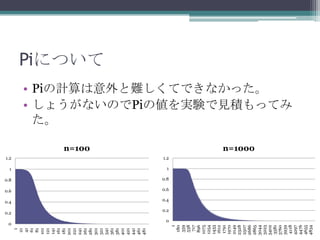
た。
161
181
201
221
241
261
n=100
281
301
321
Piについて
341
361
381
401
421
441
461
481
0.4
0.6
0.8
1
0.2
0
1.2
1
180
359
538
717
896
1075
1254
1433
1612
1791
1970
2149
2328
2507
2686
n=1000
2865
3044
3223
• Piの計算は意外と難しくてできなかった。
3402
3581
3760
3939
• しょうがないのでPiの値を実験で見積もってみ
4118
4297
4476
4655
4834

18. 0
9
4
6
10
8
1
3
5
7
2
1
19
37
55
73
91
109
127
145
163
181
199
217
235
253
271
n=100
289
307
325
343
361
379
397
415
433
451
469
487
0
4
6
8
3
5
1
7
2
1
180
359
538
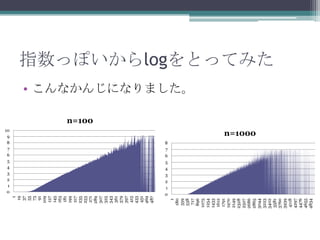
• こんなかんじになりました。
717
896
1075
1254
1433
1612
1791
1970
2149
2328
2507
2686
n=1000
2865
3044
3223
3402
指数っぽいからlogをとってみた
3581
3760
3939
4118
4297
4476
4655
4834

19. Piの値の予想
• Piはこんなかんじになりそう。
• 理由はよく分からない。

20. これを代入
1.2にわりと近くなった。

21. まとめ
• 最小全域木の大きさは約1.2に収束する。
• ↑そのことの証明はよくわからない。
• 最小全域木の辺の中で最大の辺の重みはlog n/n
程度になる。
• ↑この事の理由はよくわからない。
• n個の頂点をからなる完全無向グラフから辺をラ
ンダムに選んで部分グラフを作った時、辺の数
がn/2を超えると連結している割合が指数的に
増加する。
• ↑このことの理由もよくわからない。