研究室のゼミで発表した際の資料です．

1. 2.4 指数型分布族

2. 目次
2.4 指数型分布族
2.4.1 最尤推定と十分統計量
2.4.2 共役事前分布

3. 指数型分布族 [定義] (The Exponential Family)
𝐱上の指数型分布族は，𝜼をパラメータとし，下記で定義される分布の集合
𝐱 : スカラー，ベクトル，離散，連続どれでも可
𝜼 : 分布の自然パラメータ
𝐮 𝐱 : 𝐱の任意の関数
𝑔 𝜼 : 正規化係数
ℎ(𝐱) : 残り (今回はあまり興味ない)

4. 指数型分布族の何が嬉しいか
・モーメント(期待値や分散など)を比較的簡単に求めることが可能(2.4.1)
・パラメータの最尤推定量がデータの平均から求まる(2.4.1)
（いちいち対数尤度をパラメータで微分してゼロの計算をしなくていい）
・共役事前分布が存在する(2.4.2)

5. 指数型分布族に属する確率分布
・ベルヌーイ分布
・多項分布
・一変数ガウス分布
ベルヌーイ分布が指数型分布族に属することを確認していく

6. ベルヌーイ分布(Bernoulli distribution)
(1/2)
と比較して
を𝜇について解くと，
ロジスティックシグモイド関数

7. ∵
ベルヌーイ分布(Bernoulli distribution)
(2/2)
と比較して
1 1
1 ( ) 1 ( )
1 1 1
e
e e e

  
   

 
      
  
∴ ベルヌーイ分布は指数型分布族に属する

8. 指数型分布族に属する確率分布
・ベルヌーイ分布
・多項分布(カテゴリ分布)
・一変数ガウス分布
多項分布(カテゴリ分布)が指数型分布族に属することを確認していく

9. カテゴリ分布と多項分布
・カテゴリ分布(categorical distribution)
ベルヌーイ分布をM次元へ拡張
・多項分布(multinomial distribution)
カテゴリ分布における施行をN回繰り返す(カテゴリ分布の拡張)

10. 多項分布(multinomial distribution)
(1/4)
( 𝜼 = 𝜂1, … , 𝜂 𝑀
𝑇
)
と比較して, 𝜂 𝑘 = ln 𝜇 𝑘 とすると
( 𝐱 = 𝑥1, … , 𝑥 𝑀
𝑇 )
𝐮 𝐱 = 𝐱
ℎ 𝐱 = 1
𝑔 𝜼 = 1
より，
は独立ではない

11. 多項分布(multinomial distribution)
(2/4)
M-1個のパラメータのみで分布を表現した方が便利なこともある
と比較して

12. 多項分布(multinomial distribution)
(3/4)
代入
ソフトマックス関数
𝜂1 = 2.0, 𝜂2 = 1.5, 𝜂3 = 0.5 の時，
𝜇1 = 0.55, 𝜇2 = 0.33, 𝜇3 = 0.12
となり，出力を正規化し，確率
へと変換することができる

13. 多項分布(multinomial distribution)
(4/4)
と比較して
∴ 多項分布(カテゴリ分布)は指数型分布族に属する

14. 指数型分布族に属する確率分布
・ベルヌーイ分布
・多項分布(カテゴリ分布)
・一変数ガウス分布
一変数ガウス分布が指数型分布族に属することを確認していく

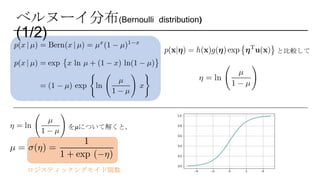
15. 一変数ガウス分布
2 2
2 2 22
2
22 2 22
1
( | , ) exp
2 22
1 1
exp exp
2 22
x x
p x
x
x
 
 
  
 
  
 
    
 
      
      
     
と比較して
∴ 一変数ガウス分布は指数型分布族に属する (多変量は演習2.57)

16. 指数型分布族に属する主な確率分布
代表的な分布 指数分布族でない分布の例
・ベルヌーイ分布 ・スチューデントの𝘁分布
・多項分布 ・混合分布
・ガウス分布
・二項分布
・ポアソン分布
・ディリクレ分布
・ウィシャート分布
・ガンマ分布
・ベータ分布
・フォンミーゼス分布
演習2.56で確認

17. 2.4.1 最尤推定と十分統計量
(Maximum likelihood and sufficient
statistics)

18. -説明の流れ-
① 十分統計量の説明
② 指数型分布族のパラメータ𝜼を求める
③ 最尤推定を用いて最尤推定量𝜼 𝑀𝐿を推定する
②と③から𝜼 𝑀𝐿が𝜼に一致することの確認

19. ある分布から得られた標本𝑋のうち，その分布のパラメータθの推定のために十
分な情報を含んだ統計量𝑇(𝑋)を十分統計量と呼び，以下の式を満たす．
パラメータ(母数)：母集団を要約する値
ex) 母集団の平均，分散 etc...
統計量𝑇(𝑋) ：標本を要約する(𝑋の)関数
ex) 標本平均，標本分散 etc...
意味：統計量𝑇(𝑋)の情報が与えられると𝑋の条件付き分布はもはやパラメータθ
に依存しない
→ つまり，ある統計量が十分であるとき，その統計量がパラメータと同
程度の価値のある情報を持っていると解釈できる
十分統計量とは

20. 指数型分布族の一般形のパラメータ𝜼を求める
(2.195) の，𝜼についての勾配を求
める
左辺2項目を右辺に移項してから両辺を(2.195)で割ると，
したがって，
(演習2.58より)
・より高次のモーメントについても同様
・指数型分布族の分布を正規化できれば，その分布のモーメントは単に微分す
れば求まる．

21. 最尤推定で指数型分布族の一般形のパラメータ𝜼を推定
データ集合‫𝐱{=܆‬1, ... , 𝐱 𝑁} ( 𝐱1, ... , 𝐱 𝑁 はi.i.d ) に対する尤
度関数
最尤推定量𝜼 𝑀𝐿が満たすべき条件 (対数尤度の𝜼についての勾配がゼロ)
(2.228)
・最尤推定量𝜼 𝑀𝐿は 𝑛 𝐮( 𝐱 𝑛)のみに依存
・ 𝑛 𝐮( 𝐱 𝑛)は十分統計量 (フィッシャーの因子分解定理)
→ 十分統計量の性質より，データ集合全体を保持する必要なし
最尤推定では十分統計量の値のみを保持すれば良い
𝑁→∞なら(2.228)の右辺は大数の法則より𝔼 𝐮 𝐱 (𝜼 𝑀𝐿は真の値𝜼に一致)

22. 2.4.2 共役事前分布(Conjugate priors)

23. 対応関係
共役事前分布
ベルヌーイ，二項分布 ベータ分布
多項分布 ディリクレ分布
一変数ガウス分布(平均未知) 一変数ガウス分布
一変数ガウス分布(精度未知) ガンマ分布
一変数ガウス分布(両方未知) ガウス-ガンマ分布
多変量ガウス分布(平均未知) 多変量ガウス分布
多変量ガウス分布(精度未知) ウィシャート分布
多変量ガウス分布(両方未知) ガウス-ウィシャート分布

24. え
指数型分布族の共役事前分布
指数型分布族の任意の分布について以下の形の共役事前分布が存在
: 正規化係数
尤度関数 と共役事前分布の積
𝜈 : 有効な事前の仮想観測値の数と解釈
は確かに事前分布の形